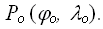Классы проекций по способу построения

Классификация картографических проекций

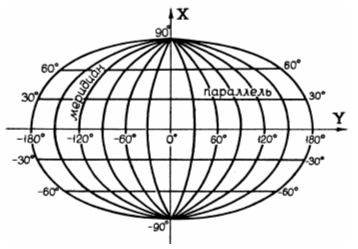
Все картографические проекции классифицируются по ряду признаков, в том числе, по характеру искажений, виду меридианов и параллелей нормальной картографической сетки, положению полюса нормальной системы координат.

1. Классификация картографических проекций

по характеру искажений:

а) равноугольные, или конформные оставляют без искажений углы и форму контуров, но имеют значительные искажения площадей. Элементарная окружность в таких проекциях всегда остается окружностью, но размеры ее сильно меняются. Такие проекции особенно удобны для определения направлений и прокладки маршрутов по заданному азимуту, поэтомy их всегда используют на навигационных картах.,

Эти проекции могут быть описаны уравнениями в характеристиках вида:

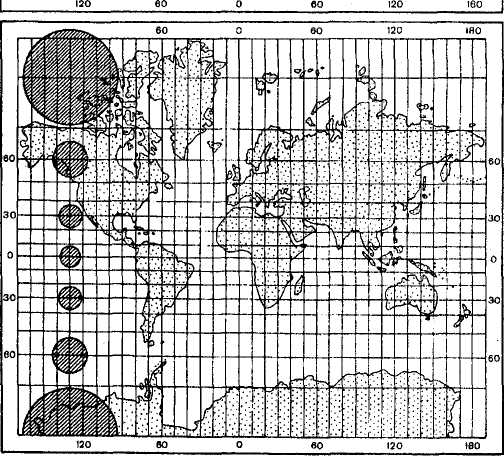
Рис. Искажения в равноугольной проекции. Карта мира в проекции Меркатора

б) равновеликие, или эквивалентные — сохраняют площади без искажений, однако на них значительно нарушены углы и формы, что особенно заметно на больших территориях. Например, на карте мира приполярные области выглядят сильно сплющенными. Эти проекции могут быть описаны уравнениями вида Р = 1.

Рис. Искажения в равновеликой проекции. Карта мира в проекции Меркатора

в) равнопромежуточные (эквидистантные).

В этих проекциях линейный масштаб по одному из главных направлений постоянен и обычно равен главному масштабу карты, т. е. имеет место

Не сохраняют ни углов, ни площадей.

2. Классификация картографических проекций по способу построения

Вспомогательными поверхностями при переходе от эллипсоида или шара к карте могут быть плоскость, цилиндр, конус, серия конусов и некоторые другие геометрические фигуры.

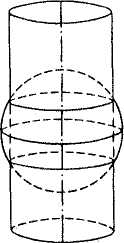
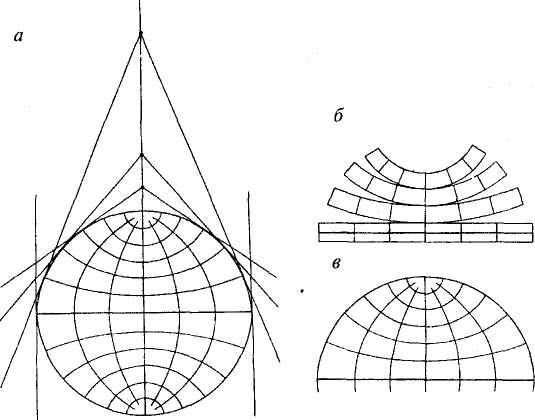
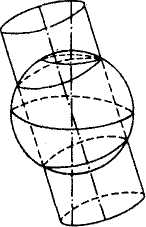
1) Цилиндрические проекции — проектирование шара (эллипсоида) ведется на поверхность касательного или секущего цилиндра, а затем его боковая поверхность разворачивается в плоскость.

В этих проекциях параллели нормальных сеток есть прямые параллельные линии, меридианы – также прямые линии, ортогональные к параллелям. Расстояния между меридианами равны и всегда пропорциональны разности долгот

Рис. Вид картографической сетки цилиндрической проекции

Условные проекции — проекции, для которых нельзя подобрать простых геометрических аналогов. Их строят, исходя из каких-либо заданных условий, например желательного вида географической сетки, того или иного распределения искажений на карте, заданного вида сетки и др., полученные путем преобразования одной или нескольких сходных проекций.

Псевдоцилиндрические проекции: параллели изображаются прямыми параллельными линиями, меридианы – кривыми линиями, симметричными относительно среднего прямолинейного меридиана, который всегда ортогонален параллелям (применяют для карт мира и Тихого океана).

Рис. Вид картографической сетки псевдоцилиндрической проекции

Полагаем, что географический полюс совпадает с полюсом нормальной системы координат

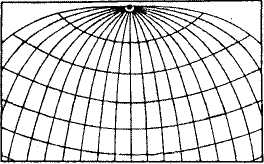
а) Нормальная (прямая) цилиндрическая — если ось цилиндра совпадает с осью вращения Земли, а его поверхность касается шара по экватору (или сечет его по па­раллелям). Тогда меридианы нормальной сетки предстают в виде равноотстоящих параллельных прямых, а параллели — в виде пря­мых, перпендикулярных к ним. В таких проекциях меньше всего искажений в тропических и приэкваториальных областях.

б) поперечная цилиндрическая проекция — ось цилиндра расположена в плоскости экватора. Цилиндр касается шара по меридиану, искажения вдоль него отсутствуют, и следовательно, в такой проекции наиболее выгодно изображать территории, вытянутые с севера на юг.

в) косая цилиндрическая — ось вспомогательного цилиндра расположена под углом к плоскости экватора. Она удобна для вытянутых территорий, ориентированных на северо-запад или северо-восток.

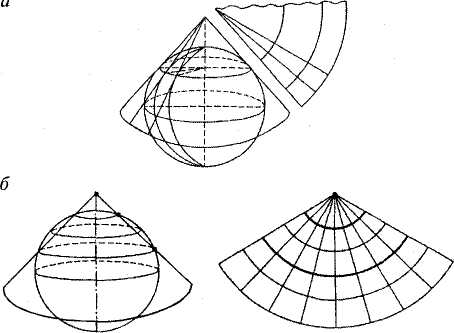
2) Конические проекции — поверхность шара (эллипсоида) проектируется на поверхность касательного или секущего конуса, после чего она как бы разрезается по образующей и разворачивается в плоскость.

Различают:

· нормальную (прямую) коническую проекцию, когда ось конуса совпа­дает с осью вращения Земли. Меридианы представляют собой прямые, расходящиеся из точки полюса, а параллели — дуги концентрических окружностей. Воображаемый конус каса­ется земного шара или сечет его в районе средних широт, поэто­му в такой проекции удобнее всего картографировать территории России, Канады, США, вытянутые с запада на восток в средних широтах.

· поперечную коническую — ось конуса нежит в плоскости экватора

· косую коническую— ось конуса на­клонена к плоскости экватора.

Псевдоконические проекции — такие, в которых все параллели изображаются дугами концентрических окружностей (как в нормальных конических), средний меридиан — прямая линия, а остальные меридианы — кривые, причем кривизна их возрастает с удалением от среднего меридиана. Применяются для карт России, Евразии, других материков.

Поликонические проекции — проекции, получаемые в результа­те проектирования шара (эллипсоида) на множество конусов. В нормальных поликонических проекциях параллели представлены дугами эксцентрических окружностей, а меридианы — кривые, симметричные относительно прямого среднего меридиана. Чаще всего эти проекции применяются для карт мира.

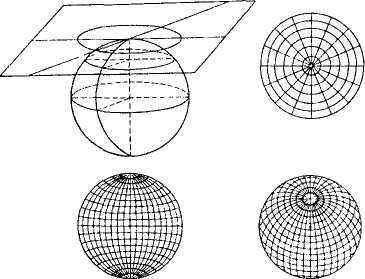
3) Азимутальные проекции — поверхность земного шара (эллип­соида) переносится на касательную или секущую плоскость. Если плоскость перпендикулярна к оси вращения Земли, то получается нормальная (полярная) азимутальная проекция. В этих проекциях параллели изображаются одноцентровыми окружностями, меридианы – пучком прямых линий с точкой схода, совпадающей с центром параллелей. В этой проекции всегда кар­тографируют полярные области нашей и других планет.

а — нормальная или полярная проекция на плоскость; в — сетка в поперечной (экваториальной) проекции;

г — сетка в косой азимутальной проекции.

Рис. Вид картографической сетки азимутальной проекции

Если плоскость проекции перпендикулярна к плоскости эква­тора, то получается поперечная (экваториальная) азимутальная проекция. Она всегда используется для карт полушарий. А если проектирование выполнено на касательную или секущую вспомогательную плоскость, находящуюся под любым углом к плоскости экватора, то получается косая азимутальная проекция.

Среди азимутальных проекций выделяют несколько их разно­видностей, различающихся по положению точки, из которой ве­дется проектирование шара на плоскость.

Псевдоазимутальные проекции — видоизмененные азимуталь­ные проекции. В полярных псевдоазимутальных проекциях парал­лели представляют собой концентрические окружности, а мери­дианы — кривые линии, симметричные относительно одного или двух прямых меридианов. Поперечные и косые псевдоазимуталь­ные проекции имеют общую овальную форму и обычно применя­ются для карт Атлантического океана или Атлантического океана вместе с Северным Ледовитым.

4) Многогранные проекции — проекции, получаемые путем про­ектирования шара (эллипсоида) на поверхность касательного или секущего многогранника. Чаще всего каждая грань представляет собой равнобочную трапецию.

3) Классификация картографических проекций по положению полюса нормальной системы координат

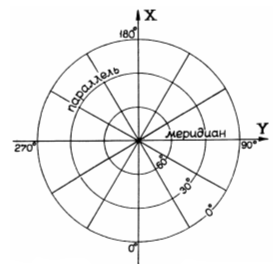
В зависимости от положения полюса нормальной системы Р_о, все проекции подразделяются на следующие:

а) прямые или нормальные – полюс нормальной системы Р_о совпадает с географическим полюсом (φ_о = 90°);

б) поперечные или экваториальные – полюс нормальной системы Р_о лежит на поверхности в плоскости экватора (φ_о = 0°);

в) косые или горизонтальные – полюс нормальной системы Р_о располагается между географическим полюсом и экватором (0°

Источник

Картографические проекции. Урок 6

Картографические проекции сегодня – это математические способы изображения всего земного эллипсоида или его части на плоскости, систематическое преобразование широт и долгот с поверхности сферы на плоскость.

Для создания географических карт выполняют две последовательных операции:

1. Перенесение (проектирование) поверхности геоида с его сложным рельефом на поверхность эллипсоида вращения или шара.
2. Дальнейшее его проектирование на плоскость (преобразование системы географических координат в декартовы) с использованием одной из картографических проекций.

При этом картографы пытаются добиться как можно меньшего количества искажений. Сделать мелкомасштабную карту совсем без искажений невозможно. На крупномасштабных (топографических) картах искажения почти отсутствуют. В зависимости от назначения карты одни погрешности допустимы, другие нет. Поэтому и существуют разные типы проекций, предназначенные для сохранения некоторых свойств сферы за счёт других её свойств.

Проекция на шар — глобус. Автор: UBC Library Digitization Centre

Виды искажений при использовании картографических проекций

Разложить на плоскости эллипс или шар очень трудно, для того, чтобы убедиться в этом, можно попробовать это сделать на практике. Сложить кусочки апельсиновой кожуры так, чтобы между ними не было пустых мест и попробовать получить непрерывную ровную плоскость. Корка соберётся в складки, она не уложится без промежутков.

При любом способе разложения шара на плоскость присутствует один или несколько типов искажения:

• базовое – искажение расстояний (длин линий), от него зависит степень других видов деформаций. Признак: между соседними параллелями отрезки меридианов неодинаковы по длине;
• площадей. При таком искажении между соседними параллелями форма и величина (а значит и площадь) ячеек неодинакова;
• углов – углы между определённым направлением на местности и на карте не совпадают. Узнать его можно по тому, что углы между параллелями и меридианами не являются прямыми;
• форм. При одинаковой площади форма клеток, находящихся на одной широте, разная.

При этом типы искажений взаимозависимы, при уменьшении одного из показателей увеличивается другой. В зависимости от назначения карты, на ней присутствуют места с нулевым искажением, с удалением от него количество искажений увеличивается. Поэтому на карте есть три вида масштаба:

• основной (тот, что подписан), действующий на линии нулевого искажения,
• частные (определяются при помощи эллипса искажений), их может быть бесконечно много;
• средний (совокупность частных масштабов отрезка).

При выборе типа картографической проекции сначала строят изоколы – изолинии, соединяющие точки с одинаковым искажением.

Изоколы искажения углов
Источник: https://ds04.infourok.ru/uploads/ex/0617/00148bfe-04623ef1/hello_html_329bd6b7.jpg

Типы проекций по характеру искажений

Для разных целей нужны карты с отсутствием тех или иных видов искажений. При помощи разных проекций можно сделать так чтобы на них отсутствовали погрешности либо углов, либо длин, либо площадей. Чем больше искажаются углы, тем меньше искажаются площади и наоборот. По характеру искажений все картографические проекции делят на:

• равноугольные (конформные);
• равновеликие (эквивалентные);
• произвольные:
  • равнопромежуточные (эквидистантные).

Равноугольные картографические проекции

На картах, построенных по этому типу, нет искажений направлений и углов. Направления на местности совпадают с таковыми на карте, прямые линии на местности остаются прямыми на карте. Они используются для прокладки точных маршрутов и применяется на навигационных и топографических картах.

Зато на них сильно изменены площади объектов Земли и линейный масштаб карты зависит от положения на ней данной точки. Типичный пример равноугольной проекции – цилиндрическая проекция Герхарда Меркатора (Герарда Кремера), созданная ещё в 1569 г и используемая в морской навигации до сих пор. Примером использования Проекции Меркатора является равноугольная проекция Гаусса-Крюгера.

В этой проекции создаются отдельные океанологические, климатические и геофизические карты.

Проекция Меркатора.
Файл доступен по лицензии: Creative Commons Attribution-Share Alike 3.0 Unported

Равновеликие картографические проекции

Это проекции для построении карт, на которых нет искажения площадей (масштаб площадей имеет везде одну и ту же величину), зато сильно растёт погрешность форм и углов (материки и океаны в высоких широтах сплющиваются). Картами, построенными в равновеликих проекциях, удобно пользоваться для расчета площадей, например типов почв, посадок кукурузы, облесенности материков, загрязнения океана или радиоактивного загрязнения суши и др.

Их применяют для составления климатических, почвенных, геофизических, геологических, зоогеографических, геоботанических, экономических, исторических, этнографических, административных карт.

Пример равновеликой проекции. Автор: CC BY-SA 3.0

Произвольные картографические проекции

Углы и площади здесь искажаются, но значительно меньше, чем в предыдущих двух проекциях. Поэтому они наиболее используемы. Произвольные картографические проекции не относятся ни к равновеликим, ни к равноугольным.

Произвольная проекция Робинсона. Автор: CC BY-SA 3.0

Равнопромежуточные картографические проекции

Это тип произвольных картографических проекций. В них масштаб длин одного из главных направлений остаётся неизменным. Пример: прямая азимутальная проекция. Равнопромежуточные проекции используют для создания общегеографических, физических, тектонических, политических и др. видов карт.

Характер искажения всегда входит в общее название проекции (равновеликая азимутальная, равноугольная коническая, равновеликая цилиндрическая и т.д.).

Интересно,

что д ревнейшей картографической проекцией является гномическая проекция, применённая на картах звёздного неба Фалесом Милетским ещё в Древней Греции.

Равнопромежуточная коническая проекция. Автор: CC BY-SA 3.0

Классификация географических проекций по геометрической фигуре, являющейся вспомогательной поверхностью

На плоскость эллипсоид проектируют при помощи геометрических фигур, а поверхности, на которые он проектируется, могут быть секущими (разрезающей) фигуру или касательными (соприкасается, но не разрезает глобус) к ней. При этом на полученной карте касательные и секущие линии (стандартные) представлены неискажёнными.

Проекции также бывают по-разному ориентированы.

• Нормальными называют проекции, в которых оси вспомогательной поверхности совмещаются с осью земного эллипсоида или шара, а спроектированная поверхность размещается касательно к полюсу.
• Поперечными – ось располагают под прямым углом к оси Земли.
• Наклонными– под любым другим (непрямым) углом к оси Земли.

Нормальная, поперечная и косая ориентации площади проекции. Автор: Rylem

Поверхности, которые могут быть развёрнуты на плоскость или лист без растяжений, разрыва или усадки, называются разрабатываемыми поверхностями. Ими являются цилиндр, конус и плоскость. Поэтому по вспомогательной поверхности проекции делятся на:

• цилиндрические – вспомогательная поверхность – боковая цилиндра, касательная к эллипсоиду или секущая эллипсоида. Меридианы изображаются равностоящими параллельными прямыми, а параллели – прямыми, перпендикулярными меридианам. Пример – нормальная равноугольная цилиндрическая проекция Меркатора.

Цилиндрическая, коническая, азимутальная типы проекций.
Автор: Rylem — собственная работа, CC BY-SA 4.0

• псевдоцилиндрические – центральный меридиан на них представлен в виде отрезка прямой, другие меридианы длиннее центрального и изогнуты наружу. Параллели псевдоцилиндрических проекций – прямые линии.

Псевдоцилиндрическая проекция

• конические – боковая поверхность секущей или касательной конуса. Конической называется любая проекция, в которой меридианы представлены прямыми линиями, выходящими из одного центра и равноудаляющимися к периферии, а параллели – дуги, центрированные на вершине. При построении картографы чаще выбирают 2 основные параллели, которые могут быть секущими или касательными. Искажения масштаба и формы на них низкие. К северу и югу от стандартных параллелей расстояния растягиваются, а между стандартными параллелями расстояния сжимаются. Может использоваться и одна стандартная параллель, тогда с удалением от неё расстояния растягиваются. Применяется для территорий, вытянутых вдоль параллелей, например, все карты России построены в конических проекциях.
• псевдоконические – проекции, где центральный меридиан – прямая, остальные меридианы кривые линии, а параллели – прямые, промежутки между которыми уменьшаются к полюсам.
• азимутальные – вспомогательной поверхностью служит секущая или касательная плоскость. Параллели на них – полные окружности. Меридианы – их радиусы. По меридианам такая проекция является равнопромежуточной и сохраняет вдоль них главный масштаб. Именно разновидностью азимутальной проекции является первая известная на Земле гномическая проекция.

Типы азимутальных проекций

• поликонические – боковые вспомогательные поверхности нескольких касательных конусов, каждая из которых затем разворачивается на плоскость. Экватор и средний меридиан – перпендикулярные прямые, параллели – дуги, выпуклостью направленные к экватору, меридианы – кривые малой кривизны, направленные выпуклой стороной от центрального меридиана.
• условные – те, что ни входят ни в один из выше перечисленных классов. Параллели и меридианы на них являются кривыми очень разного вида.

Полное название проекций может быть следующим: косая азимутальная равновеликая, нормальная равноугольная цилиндрическая, произвольная поликоническая и т.д.

Источник