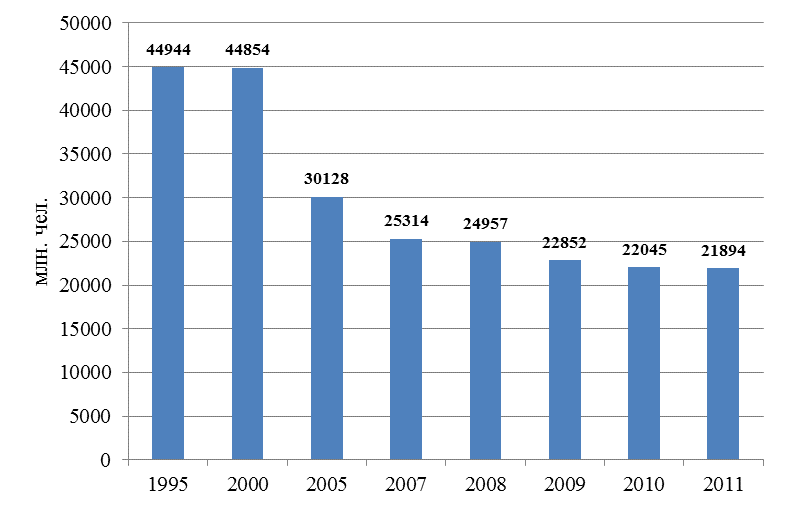Классификация статистических графиков
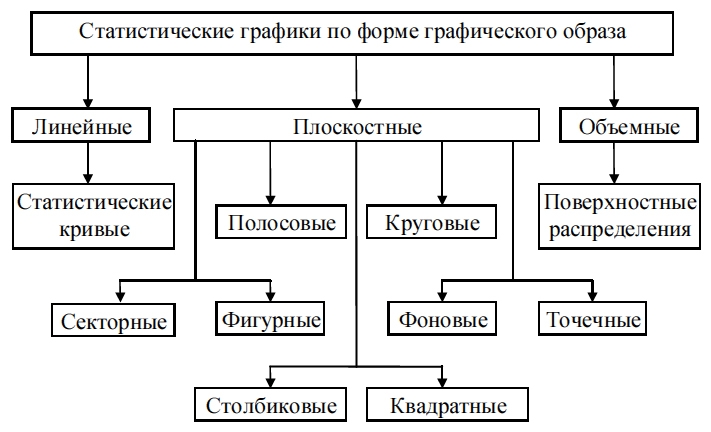
Для графического изображения статистических данных используются самые разнообразные виды графиков. При всем своем разнообразии статистические графики классифицируются по ряду признаков: способу построения, форме применяемых графических образов, характеру решаемых задач (цели использования) (рис. 5.3; 5.4).
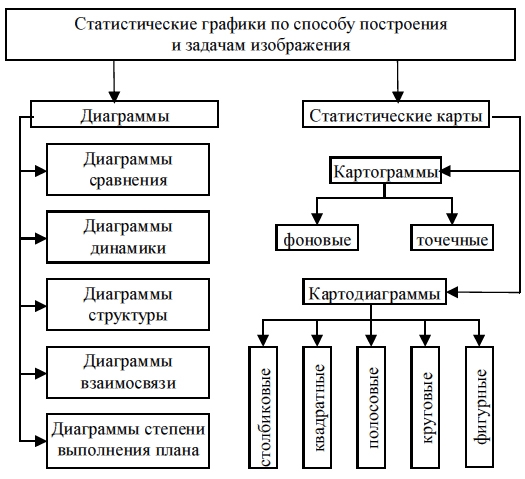
1) По способу построения:
— статистические карты: картограммы и картодиаграммы;
2) По форме применяемых графических образов: точечные, линейные, плоскостные и фигурные;
3) По цели использования: для характеристики структуры, сравнения по территориям и фирмам, оценки динамики и выполнения плана, характеристики вариации, оценки взаимосвязей.
Рис. 5.3. Классификация статистических графиков по форме графического образа
Рис. 5.4. Классификация статистических графиков
по способу построения и задачам изображения
Диаграммы
Диаграмма представляет чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков. Диаграмма – наиболее распространенный способ графических изображений. Диаграммы бывают разных видов: линейные, радиальные, точечные, плоскостные, объемные, фигурные. Вид диаграммы зависит от вида представляемых данных и задачи построения графика.
Когда число уровней в ряду динамики велико, целесообразно применять линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии. Кроме того, линейные диаграммы удобно использовать, если целью исследования является изображение общей тенденции и характера развития явления; когда на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения; если наиболее существенным является сопоставление темпов роста, а не уровней.
Для построения линейных графиков применяют систему прямоугольных координат. Обычно по оси абсцисс откладывается время (годы, месяцы и т.д.), а по оси ординат — размеры изображаемых явлений или процессов (уровни ряда динамики или темпы их изменения). Полученные точки соединяют отрезками в виде ломаной линии. Каждая точка линейной диаграммы соответствует уровню динамического ряда (или темпу его изменения) на определенный момент или за период времени.
На одном графике может быть размещено несколько диаграмм, что позволяет сравнивать динамику различных показателей, либо одного показателя по разным регионам или странам.
На оси ординат наносят масштабы. Особое внимание следует обратить на их выбор, так как от этого зависит общий вид графика. Обеспечение равновесия, пропорциональности между осями координат необходимо в графике в связи с тем, что нарушение равновесия между осями координат дает неправильное изображение развития явления. Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в динамике явлений мало выделяются, и наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колебания. Равным периодам времени и размерам уровня должны соответствовать равные отрезки масштабной шкалы.
Примеры линейных диаграмм представлены на рис. 5.5 и 5.6.
Рис. 5.6. Динамика пассажирооборота на всех видах транспорта, млрд. пасс.-км
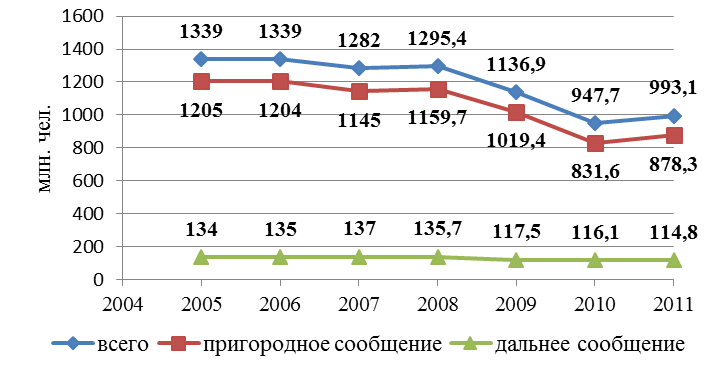
Рис. 5.6. Динамика перевозок пассажиров железнодорожным транспортом, млн. чел.
Для тех же целей, а именно анализа динамики социально-экономических явлений, оценки выполнения плана и характеристики вариации в рядах распределения могут использоваться также столбиковые диаграммы.
При построении столбиковых диаграмм используется, как и в линейных графиках, прямоугольная система координат. При этом каждое значение изучаемого показателя изображается в виде вертикального столбика. По оси абсцисс размещается основание столбиков. Их ширина может быть произвольной, но обязательно одинаковой для каждого столбика. Высота столбиков (в соответствии с принятым по оси ординат масштабом) должна строго соответствовать изображаемым данным.
Количество столбиков определяется числом изучаемых показаний (данных). Столбики могут располагаться вплотную или на одинаковом расстоянии друг от друга. У основания столбиков дается название изучаемого показателя. Уровни (величины), характеризующие значения изображаемых показателей, помещаются внутри каждого столбика.
Столбиковые диаграммы могут использоваться также для пространственных сопоставлений: сравнения по территориям, странам, фирмам, по различным видам продукции. Кроме того, столбиковые диаграммы широко используются для изучения структуры явлений.
Примеры столбиковых диаграмм представлены на рис. 5.7 и 5.8.
Рис. 5.7. Динамика перевозки пассажиров всеми видами транспорта, млн. чел.
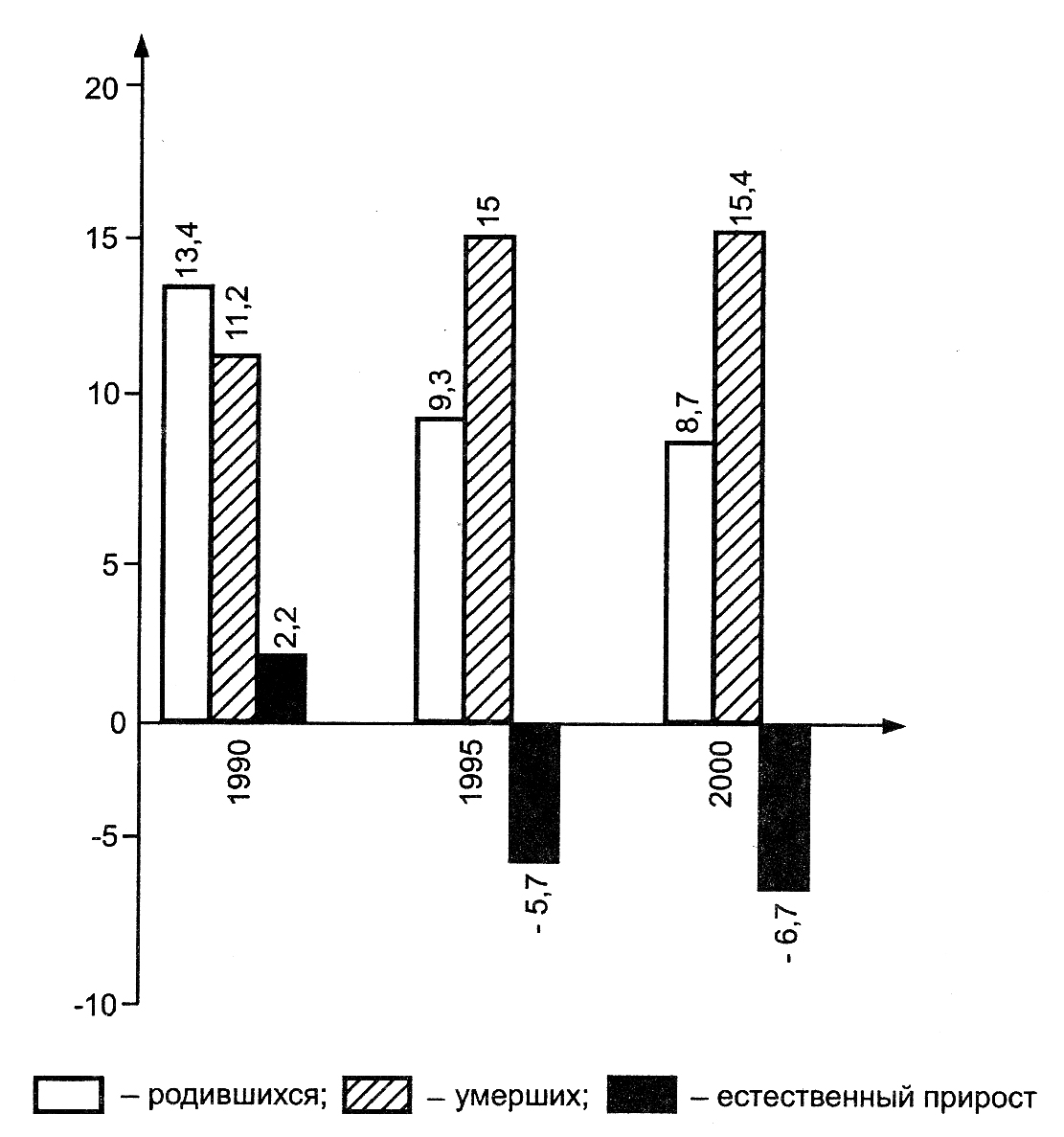
Рис. 5.8. Общие показатели рождаемости, смертности и естественного прироста
населения Российской Федерации, ‰
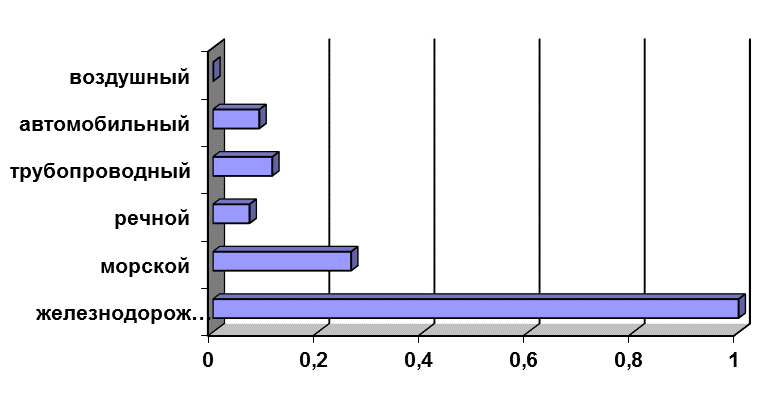
В статистике находят применение и так называемые ленточные (полосовые) графики. По своей форме ленточная диаграмма представляет ряд простирающихся по оси абсцисс полос одинаковой ширины. Длина полос (лент) соответствует значениям изображаемых показателей. При построении ленточных диаграмм соблюдаются те же требования, что и при построении столбиковых графиков (одинаковая ширина полос, начало масштабной шкалы от нулевой отметки и др.). В качестве примера полосовой диаграммы приведем графическое изображение грузооборота различных видов транспорта по отношению к грузообороту железнодорожного транспорта (относительные величины координации) (рис. 5.9).
Рис. 5.9. Соотношение грузооборота различных видов транспорта
по отношению к железнодорожному
Диаграммы, выполненные в виде выдвигающихся от начала масштабной шкалы полос, представляют определенное практическое удобство для систематического отображения хода выполнения производственных заданий нарастающим итогом.
Широкое применение для характеристики структуры социально-экономических явлений нашли секторные диаграммы. В этих диаграммах площадь окружности принимается за величину всей изучаемой статистической совокупности, а площади отдельных секторов отображают удельный вес (долю) ее составных частей. При этом поскольку площади секторов пропорциональны их центральным углам, то для построения секторной диаграммы сумма всех углов (360°) распределяется пропорционально удельным весам отдельных частей изучаемой совокупности. При процентном выражении состава изучаемой статистической совокупности исходят из соотношения 1 % = 3,6°.
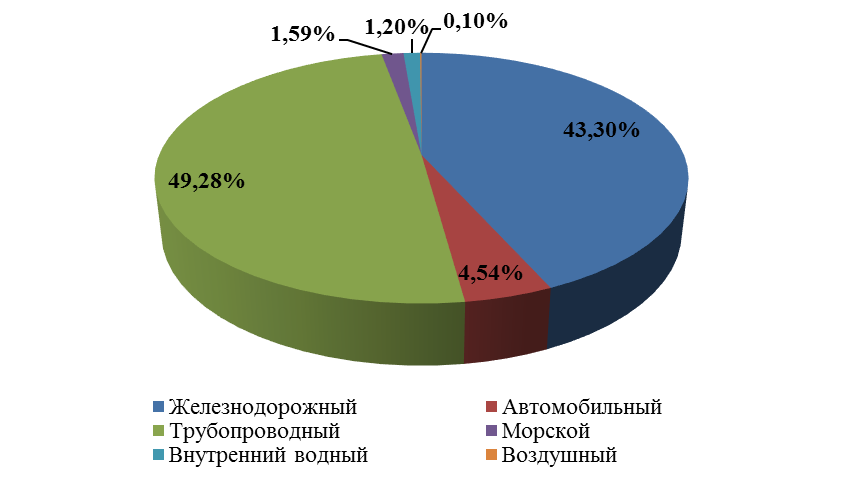
Пример секторной диаграммы представлен на рис. 5.10.
Рис. 5.10. Структура грузооборота различных видов транспорта, 2011 г.
При изучении статистической информации применяются так называемые радиальные диаграммы. Строятся они на базе полярных координат. Началом отсчета в них служит центр окружности, а носителями масштабных шкал являются радиусы круга. Обычно в основе радиальных диаграмм лежат повторяющиеся годовые циклы с помесячными или поквартальными данными. Так, при изучении годового цикла с помесячными данными окружность делят радиусами на 12 равных частей. Каждому радиусу дается название месяца года, а их расположение подобно циферблату часов. На каждом радиусе в соответствии с установленным масштабом наносятся точки, соответствующие изучаемым за каждый месяц данным. Полученные таким образом точки соединяют между собой линиями. В результате получается спиралеобразная линия, характеризующая внутригодовые циклы.
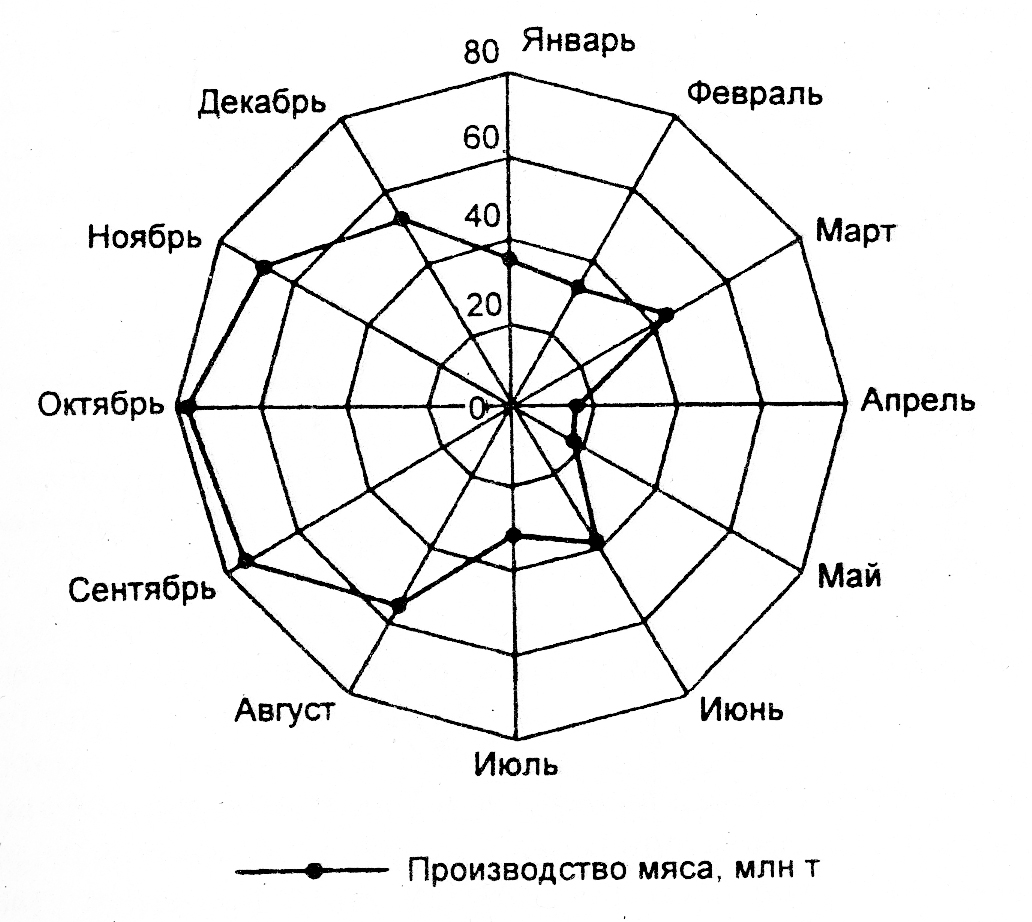
Пример радиальной диаграммы представлен на рис. 5.11.
Рис. 5.11. Производство мяса в регионе N, 2013 г.
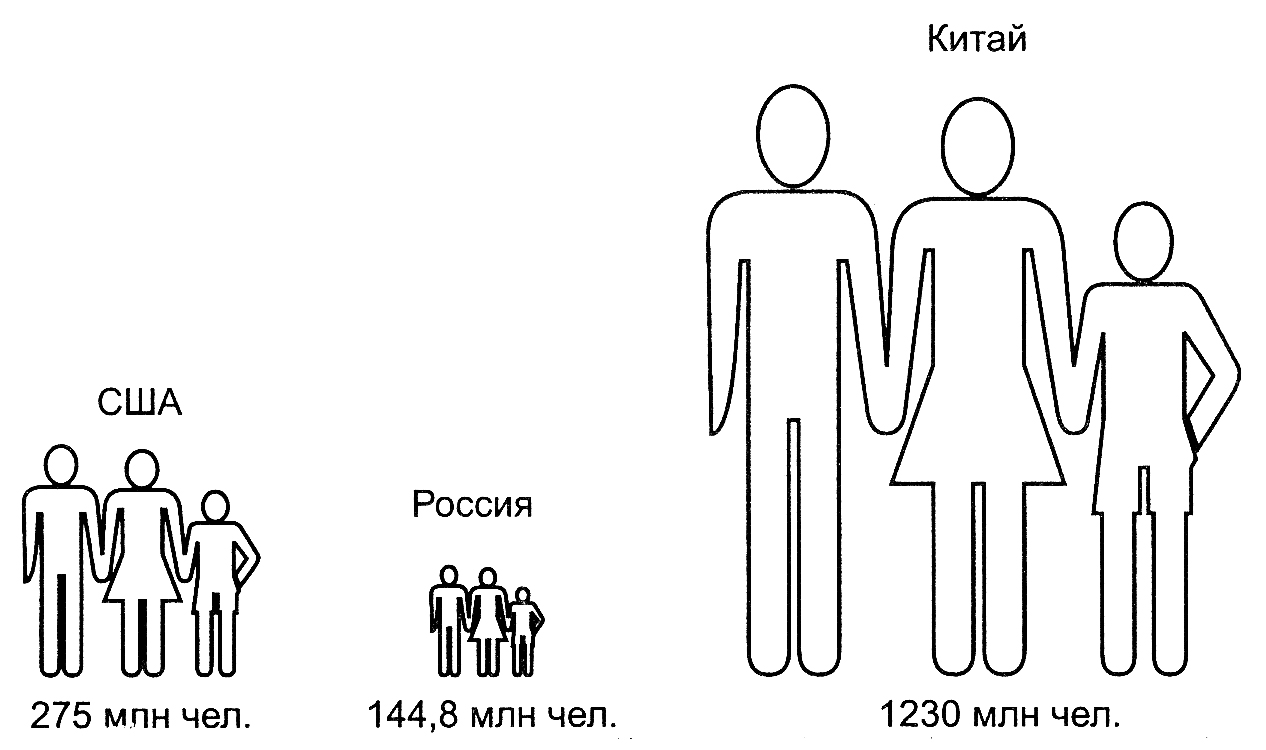
В статистике, прежде всего для рекламных целей, применяются также фигурные диаграммы. При их построении статистические данные изображаются рисунками-символами, которые в наибольшей степени соответствуют существу отображаемых явлений. Эти диаграммы более выразительны, легко воспринимаются зрительно. В фигурных статистических показателях каждому знаку символу условно придается определенное числовое значение, и путем последовательного их расположения на поле графика формируются соответствующие полосы.
Площадь фигуры соответствует величине показателя. Недостатком фигурных диаграмм является то, что графическое изображение изучаемого явления знаками-символами не всегда соответствует точному значению изображаемых данных. Поэтому наряду с целыми фигурами приходится иметь дело с их частями. Это придает отображаемым показателям приближенное значение.
Примеры фигурных диаграмм представлены на рис. 5.12 и 5.13.
Рис. 5.12. Численность постоянного населения на конец 2002 года
Рис. 5.13. Производство мяса в регионе N
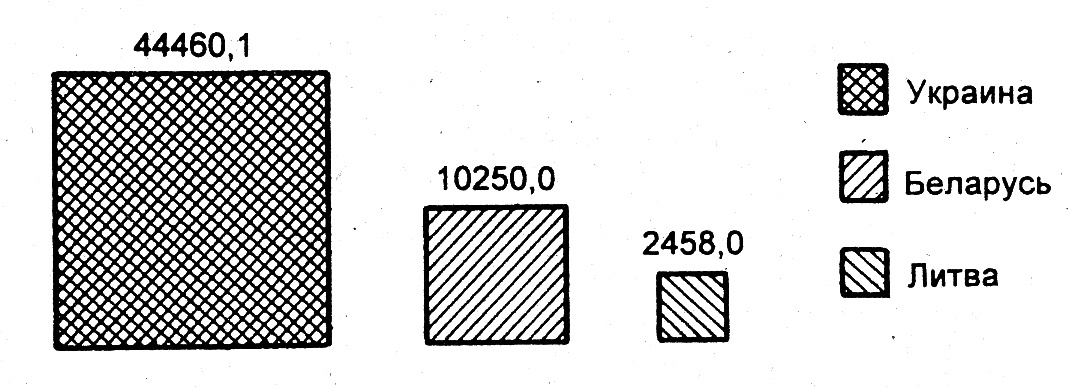
Для простого сравнения независимых друг от друга показателей могут также использоваться круговые, квадратные, прямоугольные диаграммы. Принцип их построения состоит в том, что площади правильных геометрических фигур выражают величины изображаемых явлений.
Примеры квадратных и круговых диаграмм представлены на рис. 5.14 и 5.15.
Рис. 5.14. Квадратная диаграмма поставки российского газа в страны ближнего зарубежья,
январь-август 1995 г.
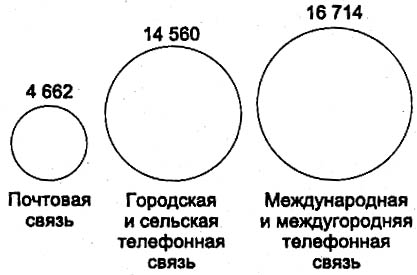
Рис. 5.15. Круговая диаграмма доходов от услуг связи
населению Российской Федерации, 2000 г.
Источник
Классификация статистических графиков
Поможем написать любую работу на аналогичную тему
При всем своем многообразии статистические графики в курсе «Статистика» классифицируются по ряду признаков: способу построения, форме применяемых графических образов, характеру решаемых задач.
По способу построения статистические графики подразделяются на диаграммы, картограммы и картодиаграммы.
Диаграмма представляет собой чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков.
Диаграмма сравнения показывает соотношение признака статистической совокупности.
На рис. 7.1 отображены доли иностранных инвестиций в экономику России на 1 января 2005 г. График отчетливо показывает страны с наибольшими (Германия, Кипр, Великобритания) и наименьшими (Италия, Финляндия) долями инвестиций.
Рис. 7.1. Столбиковая диаграмма сравнения
Каждое значение изучаемого показателя изображается в виде вертикального столбика. Количество столбиков определяется числом изучаемых показателей (данных). Расстояние между столбиками должно быть одинаковым. У основания столбиков дается название изучаемого показателя.
В этих диаграммах основания столбиков располагаются вертикально. Должна быть одинаковая ширина полос.
Эту же диаграмму можем построить иначе: с помощью полосовой диаграммы (рис. 7.2).
Рис. 7.2. Полосовая диаграмма сравнения
При построении столбиковых диаграмм используется, как и в линейных графиках, прямоугольная система координат.
По оси абсцисс размещается основание столбиков. Их ширина может быть произвольной, но обязательно одинаковой для каждого столбика.
Основные требования построения данных диаграмм:
■ соответствие столбиков по высоте, а полос ¾ по длине, отображаемым цифрам;
■ недопустимость разрывов масштабной шкалы и начала ее не от нулевой отметки.
Структурная диаграмма позволяет сопоставить статистические совокупности по составу (рис. 7.3).
Рис. 7.3. Структурно-столбиковая диаграмма,
характеризующая структуру капитала стран
Центральной и Восточной Европы на 1 января 2005 г.
Секторная диаграмма строится таким образом, чтобы каждый сектор занимал площадь круга пропорционально удельному весу отображаемых частей целого (рис. 7.4). Затем необходимо найти значения центральных углов (1% = 3,6 градуса).
Рис. 7.4. Структурно-секторная диаграмма.
Объем иностранных инвестиций, привлеченный
различными округами Российской Федерации на 1 января 2005 г.
При изучении статистической информации о социально-экономических процессах и явлениях применяются так называемые радиальные диаграммы. Строятся они на базе полярных координат. Началом отсчета в них служит центр окружности, а носителем масштабных шкал являются радиусы круга. Обычно в основе радиальных диаграмм лежат повторяющиеся годовые циклы с помесячными или поквартальными данными. Так, при изучении годового цикла с помесячными данными окружность делят радиусами на 12 равных частей. Каждому радиусу дается название месяца года, а их расположение подобно циферблату часов. На каждом радиусе в соответствии с установленным масштабом наносятся точки, соответствующие изучаемым за каждый месяц данным. Полученные таким образом точки соединяются между собой линиями. В результате получается спиралеобразная линия, характеризующая внутригодовые циклы коммерческой деятельности.
Диаграмма динамики показывает изменение явления во времени. Такая диаграмма может быть изображена с помощью уже рассмотренных типов диаграмм.
Диаграмма связи показывает функциональную зависимость одного признака от другого ¾ обычный график на координатной сетке: y = f (x) (рис. 7.5).
Рис. 7.5. Динамика грузоперевозок в Российской Федерации
за период 2001-2004 гг.
Статистическая карта ¾ вид графика, который иллюстрирует содержание статистических таблиц, где подлежащим является административное или географическое деление совокупности. На лист изображения наносится контурная географическая карта, отражающая деление совокупности на группы. Статистическая карта называется картограммой, вся информация на ней отображается в виде штриховки, линий, точек, окраски, отражающих изменение какого-либо показателя.
На картодиаграмме на фоне карты присутствуют элементы диаграммных фигур. Преимущество картодиаграммы перед диаграммой состоит в том, что она не только дает представление о величине изучаемого показателя на различных территориях, но и изображает пространственное размещение изучаемого показателя.
В зависимости от формы применяемых графических образов статистические графики могут быть точечными, линейными, плоскостными и фигурными.
В точечных графиках в качестве графических образов применяется совокупность точек.
В линейных графиках графическими образами являются линии.
Плоскостные графики изображают на трехмерной плоскости.
Для фигурных графиков графическими образами служат геометрические фигуры: прямоугольники, квадраты, окружности.
При обработке и отображении экспериментальных данных, в которых изучаемый признак может принимать любое значение из некоторого интервала, используют следующие способы представления данных:
■ полигон накопленных частот (кумулята).
Гистограмма состоит из примыкающих друг к другу прямоугольников, изображенных на координатной сетке.
При построении гистограмм могут возникнуть следующие случаи.
1. Равные интервалы группировки данных.
Рассмотрим на примере.
Имеются данные о группировке рабочих по стажу лет, (табл. 7.1).
Группы рабочих по стажу
Построим гистограмму (рис. 7.6).
Рис. 7.6. Распределение рабочих по стажу лет
На рисунке откладываются прямоугольники с высотой, прямо пропорциональной частоте данного интервала.
Наибольшее число рабочих имеют стаж работы от 5 до 7 лет.
2. Открытые крайние интервалы группировки.
Предположим, что первый и последний интервалы открытые. В таких случаях используется стандартный прием. Условно ширина первого открытого интервала принимается равной ширине следующего интервала. Ширина последнего принимается равной ширине предыдущего (табл. 7.2).
Группы рабочих по стажу
В данном случае гистограмма будет такой же, как на рис. 7.7.
3. Неравные интервалы группировки.
Предположим, что вместо двух интервалов (3-5 и 5-7) имеется один. Интервал стал шире в 2 раза, а высота стала не 27, а 13,5, с тем, чтобы площадь прямоугольника не менялась. Высоту прямоугольника можно определить по формуле:
где n ¾ частоты попадания (27);
h ¾ количество интервалов (2).
Полигон частот ¾ ломаная линия, соединяющая точки, соответствующие срединным значениям интервалов группировки и частотам интервалов.
Полигон частот получается из гистограммы, если соединить середины вершин прямоугольников ломаной линией.
Полигон накопительных частот. В данном случае для построения используются накопленные частоты. Построим полигон (рис. 7.7).
Рис. 7.7. Распределение рабочих по стажу лет
Источник