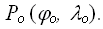Классификация проекций по способу построения

НАВИГАЦИЯ. Глава 3. §19 Классификация картографических проекций.

§19 Классификация картографических проекций.

Картографические проекции можно классифицировать по различным признакам. Однако с точки зрения построения и практического использования карт, наиболее употребительными признаками их классификации служат:

• характер искажений проекций, обусловливающий возможности практического использования карт;

• вид меридианов и параллелей нормальной сетки.

По характеру искажений

все картографические проекции делятся на четыре группы:

• равноугольные, или конформные;

• равновеликие, или эквивалентные (равноплощадные);

Равноугольные проекции

Основным свойством равноугольных, или конформных, проекций является сохранение подобия малых фигур на карте соответствующим фигурам на поверхности Земли.

Равноугольные проекции не искажают углов. Бесконечно малый круг на такой проекции изображается также кругом.

Однако, при сохранении неискаженными углов и направлений, в равноугольной проекции искажаются линейные размеры и площади фигур. Масштаб в таких проекциях зависит от направления. Эллипсы искажений, обращаясь во всех точках карты в окружности, имеют размеры, зависящие от положения точки.

Постоянство частного масштаба в данной точке по всем направлениям облегчает производство измерений на карте, составленной в равноугольной проекции. Для учета изменения масштаба при измерении больших отрезков их следует измерять на карте по частям.

Свойство конформности позволяет на картах, составленных в таких проекциях, измерять углы и азимуты непосредственно с помощью транспортира. Эти свойства обусловили широкое применение равноугольных проекций для построения морских карт. Отметим, что равноугольные проекции сохраняют равными углы, но не кривизну линий, поэтому подобие сохраняется только для малых фигур.

К равноугольным проекциям относятся проекции Меркатора, Гаусса, стереографическая и некоторые другие.

Равновеликие проекции

Равновеликие, или эквивалентные, проекции не обладают свойством подобия фигур, но сохраняют масштаб площадей в пределах всей карты одинаковым. Это означает, что равным между собой площадям на местности соответствуют равные между собой площади на карте.

Бесконечно малый на местности изобразится на карте в равновеликой проекции эллипсом, площадь которого равна площади кружка на глобусе. Любая замкнутая фигура произвольных размеров на глобусе изобразится на проекции не подобной, но равновеликой ей замкнутой фигурой. Формы эллипсов искажений в разных точках карты будут различными, площади же их обязательно будут равны площадям соответствующих кружков на глобусе.

На картах, составленных в равновеликих проекциях, можно измерять площади и сопоставлять их. Свойство равновеликости сохраняется независимо от размеров картографируемых участков. Поэтому измерения можно производить и на больших площадях.

Равнопромежуточные проекции

Равнопромежуточными называются проекции, сохраняющие постоянство масштаба по одному из главных направлений.

Вследствие этого бесконечно малый круг поверхности глобуса изобразится на плоскости проекции эллипсом, у которого одна из осей, сохранив величину, останется равной радиусу этого круга.

Произвольные проекции

Проекции, не относящиеся ни к одной из рассмотренных групп, но обладающие какими-либо другими, важными для практики свойствами, называются произвольными.

К числу наиболее часто используемых, произвольных проекций можно отнести центральную перспективную проекцию, на которой дуги больших кругов изображаются прямыми линиями.

По виду меридианов и параллелей нормальной картографической сетки

проекции делятся на следующие основные группы:

Из всех перечисленных здесь рассматриваются лишь те виды проекций, которые используются или могут использоваться для построения морских карт.

Конические проекции

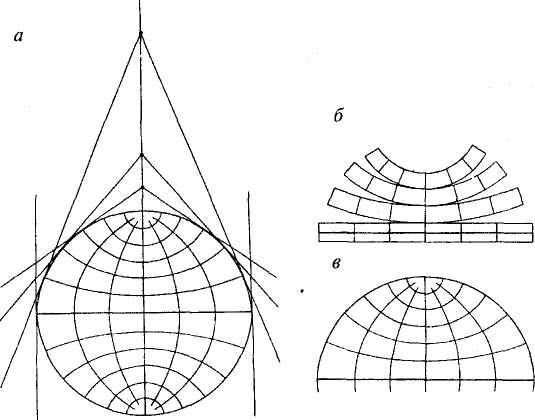
Коническими называются проекции, у которых меридианы нормальной сетки изображаются прямыми, сходящимися в общей точке под углами, пропорциональными разности долгот, а параллели нормальной сетки изображаются концентрическими окружностями, имеющими общий центр в точке пересечения меридианов.

Название конических такие проекции получили оттого, что они могут быть получены не только аналитически, но и путем геометрического проектирования поверхности глобуса на поверхность касательного или секущего глобус конуса, ось которого совпадает с географической осью глобуса.

Проектирование при этом осуществляется из точки зрения, находящейся на оси конуса. На параллели, по которой поверхность конуса касается глобуса (а также на параллелях сечения глобуса конусом), масштаб равен единице. С удалением от параллели касания в обе стороны масштаб возрастает. При проектировании на секущий конус масштаб между параллелями сечения будет меньше масштаба глобуса. т. е. меньше главного масштаба.

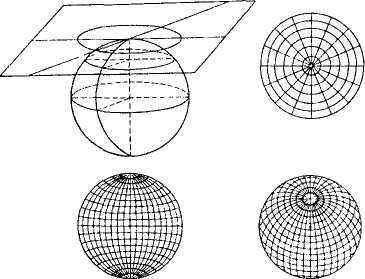
Азимутальные проекции

Азимутальными называются проекции, у которых меридианы нормальной сетки изображаются прямыми линиями, исходящими из общего центра, под углами, равными соответствующим углам между меридианами на глобусе, а параллели имеют вид концентрических окружностей с центром в точке схождения меридианов

Из приведенного определения видно, что азимутальные проекции являются частным случаем конических проекций.

Точка схождения меридианов в азимутальных проекциях является изображением полюса нормальной системы координат. Свойствами азимутальных проекций являются: равноугольность, равновеликость или равнопромежуточность.

К классу азимутальных проекций относятся перспективные проекции, получающиеся путем проектирования точек поверхности глобуса (шара) на картинную плоскость лучами, исходящими из постоянной точки.

Эта точка называется точкой зрения.

Картинная плоскость может или касаться поверхности проектируемого глобуса, или находиться от него на некотором удалении, или пересекать ее. Точка зрения выбирается на перпендикуляре к картинной плоскости, проходящем через центр проектируемого глобуса.

В зависимости от расположения точки зрения относительно центра глобуса перспективные проекции делятся:

— на ортографические, когда точка зрения удалена в бесконечность;

— на внешние, когда точка зрения находится на конечном расстоянии от центра проектируемого глобуса, но далее точки, представляющей антипод полюса нормальной системы координат;

— на стереографические, когда расстояние от центра глобуса до точки зрения равно радиусу глобуса, т.е. когда точка зрения помещается в точке шара, противоположной полюсу нормальной системы координат (в точке — антиподе полюса нормальной системы координат);

— на центральные (гномонические), когда точка зрения помещена в центре глобуса.

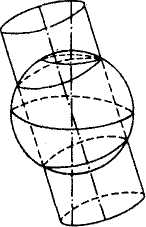
Цилиндрические проекции

Цилиндрическими проекциями называются такие, параллели и меридианы нормальной сетки которых изображаются взаимно перпендикулярными прямыми.

Удаление параллелей сетки от экватора является функцией широты, расстояния между меридианами пропорциональны разностям долгот.

Общие уравнения цилиндрических проекций имеют вид:

x = f (φ); y = C λ

Вид функции x = f (φ) и коэффициент С определяют важнейшие свойства цилиндрической проекции. Изменяя их, можно получить равноугольную, равнопромежуточную, равновеликую или произвольную проекцию. Цилиндрические проекции могут быть получены путем проектирования поверхности глобуса на касательный или секущий глобус цилиндр. При проектировании на касательный по экватору цилиндр масштаб вдоль экватора сохраняет равенство главному масштабу, т.е. экватор глобуса изображается на проекции без искажений. При проектировании на секущий цилиндр линиями нулевых искажений будут являться параллели сечения.

Из цилиндрических наиболее употребительны в кораблевождении прямая и поперечная проекции Меркатора и поперечная проекция Гаусса.

Источник

«Классификация картографических проекций и виды проекций «

Описание презентации по отдельным слайдам:

Классификация картографических проекций

Математически определенный способ отображения поверхности Земли (либо другого небесного тела, или в общем смысле, любой искривлённой поверхности) на плоскость. Определение:

— равноугольные, или конформные; — равновеликие, или эквивалентные (равноплощадные); — равнопромежуточные (эквидистантные); — произвольные. Классификация по характеру искажений:

Равноугольные проекции. Основным свойством равноугольных, или конформных, проекций является сохранение подобия малых фигур на карте соответствующим фигурам на поверхности Земли. Равноугольные проекции не искажают углов. Бесконечно малый круг на такой проекции изображается также кругом. Однако при сохранении неискаженными углов и направлений в равноугольной проекции искажаются линейные размеры и площади фигур. Масштаб в таких проекциях зависит от направления. Эллипсы искажений, обращаясь во всех точках карты в окружности, имеют размеры, зависящие от положения точки. Условие равноугольности картографической проекции можно записать следующим образом: a = b; m = n.

Равновеликие проекции. Равновеликие, или эквивалентные, проекции не обладают свойством подобия фигур, но сохраняют масштаб площадей в пределах всей карты одинаковым. Это означает, что равным между собой площадям на местности соответствуют равные между собой площади на карте. Бесконечно малый кружок на местности изобразится на карте в равновеликой проекции эллипсом, площадь которого равна площади кружка на глобусе. Любая замкнутая фигура произвольных размеров на глобусе изобразится на проекции не подобной, но равновеликой ей замкнутой фигурой. Формы эллипсов искажений в разных точках карты будут различными, площади же их обязательно будут равны площадям соответствующих кружков на глобусе. Математическое условие равновеликости можно записать следующим образом: p = ab = 1. На картах, составленных в равновеликих проекциях, можно измерять площади и сопоставлять их. Свойство равновеликости сохраняется независимо от размеров картографируемых участков. Поэтому измерения можно производить и на больших площадях.

Равнопромежуточные проекции. Равнопромежуточными называются проекции, сохраняющие постоянство масштаба по одному из главных направлений. Вследствие этого бесконечно малый круг поверхности глобуса изобразится на плоскости проекции эллипсом, у которого одна из осей, сохранив величину, останется равной радиусу этого круга. Таким образом, основное условие равнопромежуточных проекций выражается так: а=1 или b= 1; р = а или р = b. Искажение углов и площадей в равнопромежуточной проекции выражается формулами: sin ω = (a — 1) : (a + 1); vp = a — 1. где vр — увеличение масштаба площадей.

Произвольные проекции. Проекции, не относящиеся ни к одной из рассмотренных групп, но обладающие какими-либо другими, важными для практики свойствами, называются произвольными. К числу наиболее часто используемых, произвольных проекций можно отнести центральную перспективную проекцию, на которой дуги больших кругов изображаются прямыми линиями.

— конические; — азимутальные; — цилиндрические; Классификация виду меридианов и параллелей нормальной картографической сетки проекции

Конические проекции. Коническими называются проекции, у которых меридианы нормальной сетки изображаются прямыми, сходящимися в общей точке под углами, пропорциональными разности долгот, а параллели нормальной сетки изображаются концентрическими окружностями, имеющими общий центр в точке пересечения меридианов (рисунок). Конические проекции определяются уравнениями: λ = α λo ρ = f (φ) (74) где λ — разность долгот на проекции; α — коэффициент пропорциональности (обычно меньше единицы), называемый показателем конической проекции; λо — угол между меридианами в натуре; ρ — радиус параллели сетки. Название конических такие проекции получили оттого, что они могут быть получены не только аналитически, но и путем геометрического проектирования поверхности глобуса на поверхность касательного или секущего глобус конуса, ось которого совпадает с географической осью глобуса. Проектирование при этом осуществляется из точки зрения, находящейся на оси конуса. На параллели, по которой поверхность конуса касается глобуса (а также на параллелях сечения глобуса конусом), масштаб равен единице. С удалением от параллели касания в обе стороны масштаб возрастает. При проектировании на секущий конус масштаб между параллелями сечения будет меньше масштаба глобуса.

Азимутальные проекции. Азимутальными называются проекции, у которых меридианы нормальной сетки изображаются прямыми линиями, исходящими из общего центра, под углами, равными соответствующим углам между меридианами на глобусе, а параллели имеют вид концентрических окружностей с центром в точке схождения меридианов (рисунок-круг). Уравнения меридианов и параллелей нормальной сетки в азимутальных проекциях имеют вид δ = λo ρ = f (φ) (75) где δ —угол между меридианами нормальной сетки; λo — угол между меридианами на глобусе; ρ —-радиус параллели .нормальной сетки.

Цилиндрические проекции. Цилиндрическими проекциями называются такие, параллели и меридианы нормальной сетки которых изображаются взаимно перпендикулярными прямыми. Удаление параллелей сетки от экватора является функцией широты, расстояния между меридианами пропорциональны разностям долгот. Общие уравнения цилиндрических проекций имеют вид x = f (φ) y = C λ (76)

Источник

Классификация картографических проекций

Все картографические проекции классифицируются по ряду признаков, в том числе, по характеру искажений, виду меридианов и параллелей нормальной картографической сетки, положению полюса нормальной системы координат.

1. Классификация картографических проекций

по характеру искажений:

а) равноугольные, или конформные оставляют без искажений углы и форму контуров, но имеют значительные искажения площадей. Элементарная окружность в таких проекциях всегда остается окружностью, но размеры ее сильно меняются. Такие проекции особенно удобны для определения направлений и прокладки маршрутов по заданному азимуту, поэтомy их всегда используют на навигационных картах.,

Эти проекции могут быть описаны уравнениями в характеристиках вида:

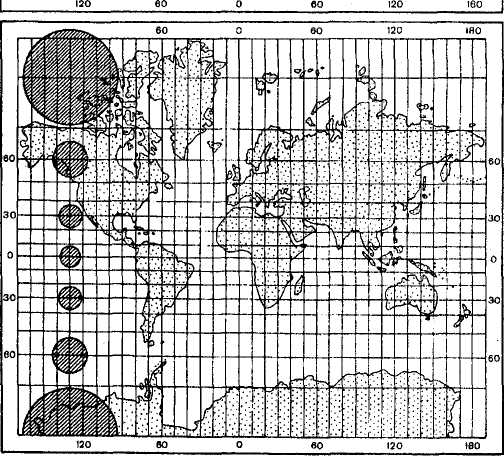
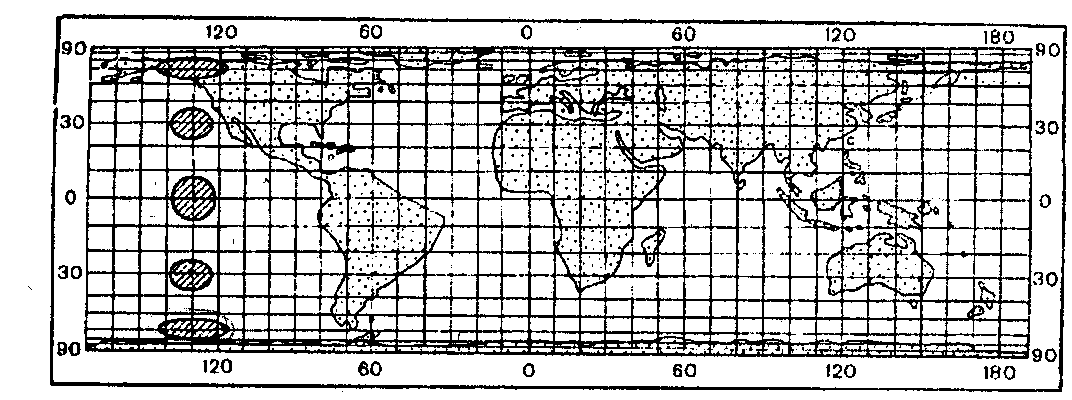
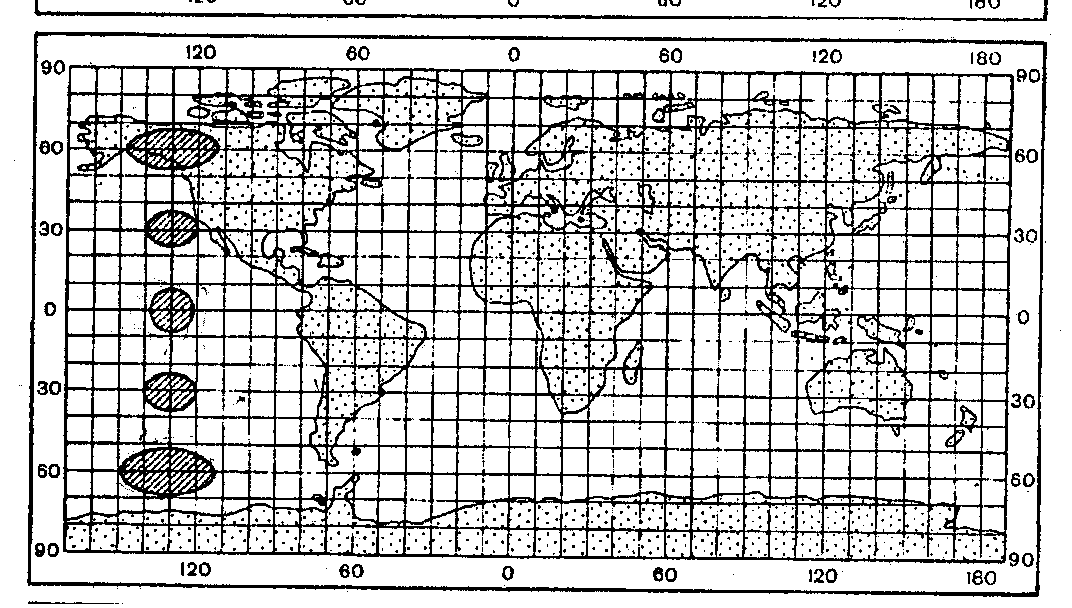
Рис. Искажения в равноугольной проекции. Карта мира в проекции Меркатора

б) равновеликие, или эквивалентные — сохраняют площади без искажений, однако на них значительно нарушены углы и формы, что особенно заметно на больших территориях. Например, на карте мира приполярные области выглядят сильно сплющенными. Эти проекции могут быть описаны уравнениями вида Р = 1.

Рис. Искажения в равновеликой проекции. Карта мира в проекции Меркатора

в) равнопромежуточные (эквидистантные).

В этих проекциях линейный масштаб по одному из главных направлений постоянен и обычно равен главному масштабу карты, т. е. имеет место

Не сохраняют ни углов, ни площадей.

2. Классификация картографических проекций по способу построения

Вспомогательными поверхностями при переходе от эллипсоида или шара к карте могут быть плоскость, цилиндр, конус, серия конусов и некоторые другие геометрические фигуры.

1) Цилиндрические проекции — проектирование шара (эллипсоида) ведется на поверхность касательного или секущего цилиндра, а затем его боковая поверхность разворачивается в плоскость.

В этих проекциях параллели нормальных сеток есть прямые параллельные линии, меридианы – также прямые линии, ортогональные к параллелям. Расстояния между меридианами равны и всегда пропорциональны разности долгот

Рис. Вид картографической сетки цилиндрической проекции

Условные проекции — проекции, для которых нельзя подобрать простых геометрических аналогов. Их строят, исходя из каких-либо заданных условий, например желательного вида географической сетки, того или иного распределения искажений на карте, заданного вида сетки и др., полученные путем преобразования одной или нескольких сходных проекций.

Псевдоцилиндрические проекции: параллели изображаются прямыми параллельными линиями, меридианы – кривыми линиями, симметричными относительно среднего прямолинейного меридиана, который всегда ортогонален параллелям (применяют для карт мира и Тихого океана).

Рис. Вид картографической сетки псевдоцилиндрической проекции

Полагаем, что географический полюс совпадает с полюсом нормальной системы координат

а) Нормальная (прямая) цилиндрическая — если ось цилиндра совпадает с осью вращения Земли, а его поверхность касается шара по экватору (или сечет его по па­раллелям). Тогда меридианы нормальной сетки предстают в виде равноотстоящих параллельных прямых, а параллели — в виде пря­мых, перпендикулярных к ним. В таких проекциях меньше всего искажений в тропических и приэкваториальных областях.

б) поперечная цилиндрическая проекция — ось цилиндра расположена в плоскости экватора. Цилиндр касается шара по меридиану, искажения вдоль него отсутствуют, и следовательно, в такой проекции наиболее выгодно изображать территории, вытянутые с севера на юг.

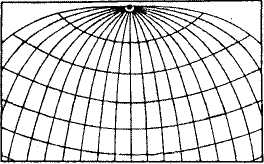в) косая цилиндрическая — ось вспомогательного цилиндра расположена под углом к плоскости экватора. Она удобна для вытянутых территорий, ориентированных на северо-запад или северо-восток.

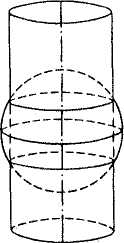
2) Конические проекции — поверхность шара (эллипсоида) проектируется на поверхность касательного или секущего конуса, после чего она как бы разрезается по образующей и разворачивается в плоскость.

Различают:

· нормальную (прямую) коническую проекцию, когда ось конуса совпа­дает с осью вращения Земли. Меридианы представляют собой прямые, расходящиеся из точки полюса, а параллели — дуги концентрических окружностей. Воображаемый конус каса­ется земного шара или сечет его в районе средних широт, поэто­му в такой проекции удобнее всего картографировать территории России, Канады, США, вытянутые с запада на восток в средних широтах.

· поперечную коническую — ось конуса нежит в плоскости экватора

· косую коническую— ось конуса на­клонена к плоскости экватора.

Псевдоконические проекции — такие, в которых все параллели изображаются дугами концентрических окружностей (как в нормальных конических), средний меридиан — прямая линия, а остальные меридианы — кривые, причем кривизна их возрастает с удалением от среднего меридиана. Применяются для карт России, Евразии, других материков.

Поликонические проекции — проекции, получаемые в результа­те проектирования шара (эллипсоида) на множество конусов. В нормальных поликонических проекциях параллели представлены дугами эксцентрических окружностей, а меридианы — кривые, симметричные относительно прямого среднего меридиана. Чаще всего эти проекции применяются для карт мира.

3) Азимутальные проекции — поверхность земного шара (эллип­соида) переносится на касательную или секущую плоскость. Если плоскость перпендикулярна к оси вращения Земли, то получается нормальная (полярная) азимутальная проекция. В этих проекциях параллели изображаются одноцентровыми окружностями, меридианы – пучком прямых линий с точкой схода, совпадающей с центром параллелей. В этой проекции всегда кар­тографируют полярные области нашей и других планет.

а — нормальная или полярная проекция на плоскость; в — сетка в поперечной (экваториальной) проекции;

г — сетка в косой азимутальной проекции.

Рис. Вид картографической сетки азимутальной проекции

Если плоскость проекции перпендикулярна к плоскости эква­тора, то получается поперечная (экваториальная) азимутальная проекция. Она всегда используется для карт полушарий. А если проектирование выполнено на касательную или секущую вспомогательную плоскость, находящуюся под любым углом к плоскости экватора, то получается косая азимутальная проекция.

Среди азимутальных проекций выделяют несколько их разно­видностей, различающихся по положению точки, из которой ве­дется проектирование шара на плоскость.

Псевдоазимутальные проекции — видоизмененные азимуталь­ные проекции. В полярных псевдоазимутальных проекциях парал­лели представляют собой концентрические окружности, а мери­дианы — кривые линии, симметричные относительно одного или двух прямых меридианов. Поперечные и косые псевдоазимуталь­ные проекции имеют общую овальную форму и обычно применя­ются для карт Атлантического океана или Атлантического океана вместе с Северным Ледовитым.

4) Многогранные проекции — проекции, получаемые путем про­ектирования шара (эллипсоида) на поверхность касательного или секущего многогранника. Чаще всего каждая грань представляет собой равнобочную трапецию.

3) Классификация картографических проекций по положению полюса нормальной системы координат

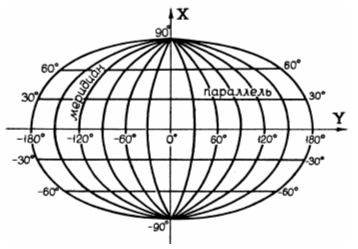
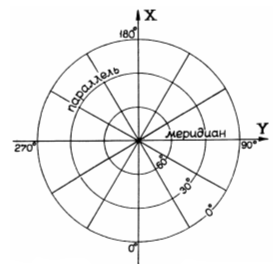
В зависимости от положения полюса нормальной системы Р_о, все проекции подразделяются на следующие:

а) прямые или нормальные – полюс нормальной системы Р_о совпадает с географическим полюсом (φ_о = 90°);

б) поперечные или экваториальные – полюс нормальной системы Р_о лежит на поверхности в плоскости экватора (φ_о = 0°);

в) косые или горизонтальные – полюс нормальной системы Р_о располагается между географическим полюсом и экватором (0°

Источник