Классификация поверхностей способы образования поверхностей
Контрольные задания по теме:
Рабочая тетрадь задача 58а, задача 58б
Мир поверхностей очень разнообразен. Они играют огромную роль в науке, архитектуре и технике. В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением типа F(x, y, z)=0, где F(x, y, z) многочлен n-й степени. Степень многочлена определяет порядок поверхности. Например, прямую линию можно назвать поверхностью первого порядка. Поверхности второго порядка – это поверхности, состоящие из плоскостей и также некоторые поверхности вращения.
Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка. Порядок поверхности также может быть определен по числу точек пересечения ее с прямой линией.
В начертательной геометрии фигуры задаются графически, поэтому поверхность рассматривается как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Она называется образующей, а линия, вдоль которой она перемещается, – направляющей. Такой способ образования поверхности называется кинематическим.
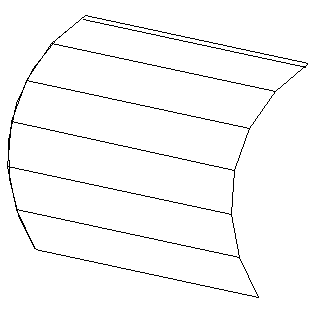
Рисунок 37
На рисунке 37 прямая линия — образующая, а дуга, вдоль которой она перемещается, — направляющая. Другим способом образования поверхности и задания ее на чертеже является задание множества принадлежащих ей точек и линий. Такой способ называется каркасным, а упорядоченное множество точек и линий поверхности называется ее каркасом.
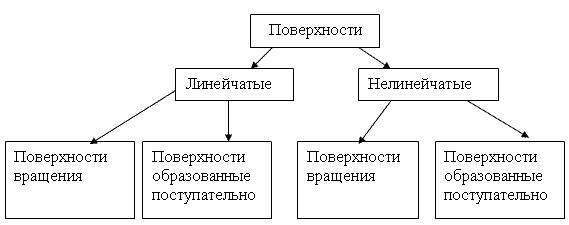
Рисунок 38
Линейчатые поверхности вращения – это конус, цилиндр.
Линейчатые поверхности поступательного движения – все гранные поверхности.
К нелинейчатым поверхностям вращения относятся сфера, шар, эллипсоид. Нелинейчатые поверхности, образованные поступательным движением – это гиперболический параболоид и другие сложные поверхности.
Образующей является прямая линия, направляющая – ломаная. Гранная поверхность представляет из себя совокупность пересекающихся плоскостей – граней. Линии пересечения граней – ребра. Точки пересечения ребер – вершины.
Наиболее простой является призматическая поверхность. Она изображена на рисунке 39. Образующая l передвигается вдоль ломаной линии m, которая является направляющей. Все образующие поверхности параллельны.

Рисунок 39
Призмой называется геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которое получается, если призматическую поверхность ограничить двумя основаниями. Основания будут иметь форму многоугольников, боковые грани параллелограммов. Если плоскости основания перпендикулярны боковым граням, то призма называется прямой, если нет то наклонной. Если в основании призмы лежит правильный многоугольник, то призма называется правильной.
Пирамидальная поверхность изображена на рисунке 40. Один конец образующей l неподвижен, а другой передвигается вдоль ломаной линии m.

Рисунок 40
Пирамидой является геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которая будет называться основанием. Точка S-вершина пирамиды. Боковые грани – треугольники. Пирамида будет называться правильной, если в основании лежит правильный многоугольник, а высота опущенная из вершины попадает в центр основания.
1. Что называется поверхностью? Какие способы образования поверхностей вы знаете?
2. Назовите линейчатые поверхности вращения.
3. Какие нелинейчатые поверхности вы знаете?
4.Какая линия является направляющей у гранных поверхностей, какая является образующей?
5. Как образуется поверхность пирамиды, призмы?
6. Какая призма называется прямой?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Источник
Классификация поверхностей способы образования поверхностей
Контрольные задания по теме:
Рабочая тетрадь задача 58а, задача 58б
Мир поверхностей очень разнообразен. Они играют огромную роль в науке, архитектуре и технике. В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением типа F(x, y, z)=0, где F(x, y, z) многочлен n-й степени. Степень многочлена определяет порядок поверхности. Например, прямую линию можно назвать поверхностью первого порядка. Поверхности второго порядка – это поверхности, состоящие из плоскостей и также некоторые поверхности вращения.
Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка. Порядок поверхности также может быть определен по числу точек пересечения ее с прямой линией.
В начертательной геометрии фигуры задаются графически, поэтому поверхность рассматривается как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Она называется образующей, а линия, вдоль которой она перемещается, – направляющей. Такой способ образования поверхности называется кинематическим.
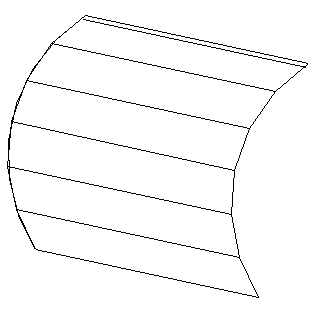
Рисунок 37
На рисунке 37 прямая линия — образующая, а дуга, вдоль которой она перемещается, — направляющая. Другим способом образования поверхности и задания ее на чертеже является задание множества принадлежащих ей точек и линий. Такой способ называется каркасным, а упорядоченное множество точек и линий поверхности называется ее каркасом.
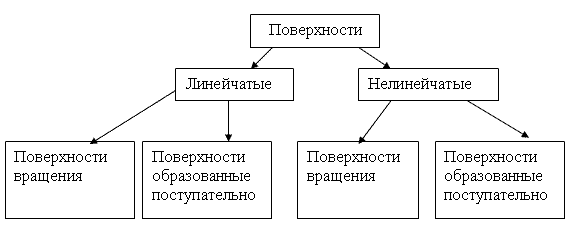
Рисунок 38
Линейчатые поверхности вращения – это конус, цилиндр.
Линейчатые поверхности поступательного движения – все гранные поверхности.
К нелинейчатым поверхностям вращения относятся сфера, шар, эллипсоид. Нелинейчатые поверхности, образованные поступательным движением – это гиперболический параболоид и другие сложные поверхности.
Образующей является прямая линия, направляющая – ломаная. Гранная поверхность представляет из себя совокупность пересекающихся плоскостей – граней. Линии пересечения граней – ребра. Точки пересечения ребер – вершины.
Наиболее простой является призматическая поверхность. Она изображена на рисунке 39. Образующая l передвигается вдоль ломаной линии m, которая является направляющей. Все образующие поверхности параллельны.
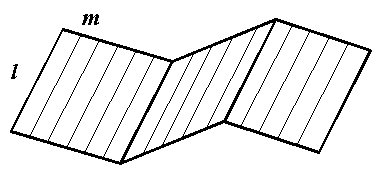
Рисунок 39
Призмой называется геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которое получается, если призматическую поверхность ограничить двумя основаниями. Основания будут иметь форму многоугольников, боковые грани параллелограммов. Если плоскости основания перпендикулярны боковым граням, то призма называется прямой, если нет то наклонной. Если в основании призмы лежит правильный многоугольник, то призма называется правильной.
Пирамидальная поверхность изображена на рисунке 40. Один конец образующей l неподвижен, а другой передвигается вдоль ломаной линии m.
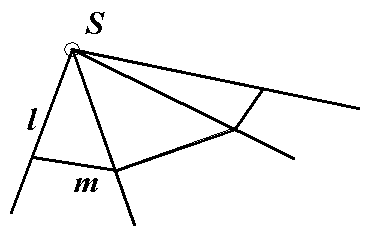
Рисунок 40
Пирамидой является геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которая будет называться основанием. Точка S-вершина пирамиды. Боковые грани – треугольники. Пирамида будет называться правильной, если в основании лежит правильный многоугольник, а высота опущенная из вершины попадает в центр основания.
1. Что называется поверхностью? Какие способы образования поверхностей вы знаете?
2. Назовите линейчатые поверхности вращения.
3. Какие нелинейчатые поверхности вы знаете?
4.Какая линия является направляющей у гранных поверхностей, какая является образующей?
5. Как образуется поверхность пирамиды, призмы?
6. Какая призма называется прямой?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Источник
Образование и классификация поверхностей



ЛЕКЦИЯ №5: Поверхности.
Поверхностью называют множество последовательных положений линии, перемещающейся в пространстве. Эта линия может быть прямой или кривой и называетсяобразующей поверхности.
Линия, с помощью которой задается направление перемещения образующей, называется направляющей.
Любую поверхность можно получить разными способами.
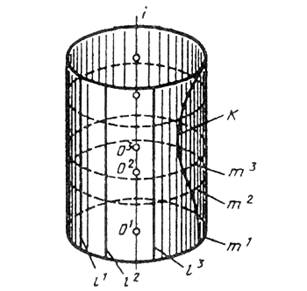
Например, прямой круговой цилиндр можно создать вращением образующей l вокруг оси I параллельной ей. А можно — перемещением окружности m, центр которой скользит по оси.
Также любая кривая k, лежащая на поверхности цилиндра, образует эту поверхность при своем вращении вокруг оси (рис. 5.1.1).
На практике из всех возможных способов образования поверхности выбирают наиболее простой.
В зависимости от формы образующей все поверхности можно разделитьна:
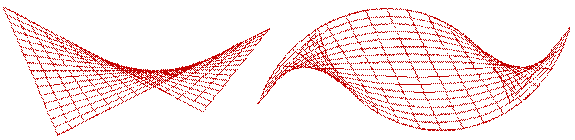
· линейчатые – образующая прямая линия (рис. 5.1.2.а);
· нелинейчатые(криволинейные) – образующая кривая линия (рис. 5.2.б).
В линейчатых поверхностях выделяют поверхности развертывающиеся, совмещаемые всеми своими точками с плоскостью без разрывов и складок, и неразвертывающиеся, которые нельзя совместить с плоскостью без разрывов и складок.
К развертывающимся поверхностям относятся:
Все остальные поверхности — неразвертывающиеся.
Источник
Теория1 / 7 Образов поверхн
1.Поверхностью называется совокупность всех последовательных положений линий, непрерывно перемещающихся в пространстве по определённому закону. Следовательно, всякую поверхность можно представить как перемещение линии по другим линиям. Линия, образующая поверхность, называется образующей. Линия, по которой перемещается образующая, называется направляющей. Образующие могут быть постоянными и изменяться.
Образование поверхностей. Поверхность можно задать на чертеже, задав её множеством принадлежащих ей точек и линий. При этом точки выбирают так, чтобы они давали возможность с достаточной степенью точности определить форму поверхности и решать на ней различные задачи.
Поверхности на комплексном чертеже могут быть заданы:
1.Проекциями направляющих и способом перемещения по ним образующих.
2.Семейством линий, принадлежащих поверхности — каркасный способ задания поверхности.
3.Очерком поверхности, т.е. линиями, ограничивающими на комплексн
2.Кинематический способ рассмотрим на примере образования цилиндрической поверхности, она образуется перемещением прямолинейной о
Если точка лежит на поверхности, то она лежит на её образующей.
В частном случае, когда направляющая ломаная, получается призматическая поверхность.
Каркасный способ образования поверхности связан с понятием определителя поверхности, которым называют совокупность независимых условий, однозначно задающих поверхность. Определитель поверхности состоит из двух частей: геометрической и алгоритмической. В геометрическую часть определителя входят геометрические фигуры и отношения между ними. В алгоритмическую часть – закон образования поверхности. Обычно определитель и закон образования поверхности представляют в определенной знаковой записи, которую называют формулой поверхности: Ф(Г)[А] , где (Г) – геометр. ч-ть; [А] –алгоритмическая.
3.Классификация поверхностей.
I. По закону образования — на закономерные и незакономерные. Закономерные задаются графически и аналитически, незакономерные — только графически.
II. По форме образующей: 1.С прямолинейными образующими — линейчатые поверхности:
(по признаку развёртывания в плоскость)
а) развёртывающиеся (плоские, торсовые);
б) не развёртывающиеся (с плоскостью параллелизма, винтовые).
2.С криволинейной образующей — кривые поверхности:
(по способу перемещения образующей)
а) с поступательным движением образующей;
б) с вращательным движением образующей — поверхности вращения;
в) с движением образующей по винтовой линии — винтовые поверхности.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Классификация поверхностей. Способы образования поверхностей?
Полагаю, вопросик восходит к начертательной геометрии.. .:-)
Многообразие форм поверхностей создает большие трудности при их изучении. Для того, чтобы обеспечить процесс изучения поверхностей, целесообразно осуществить их систематизацию, распределив все поверхности по классам и подклассам.
К сожалению невозможно разработать применяемую для всех возможных случаев классификацию поверхностей. Внутри каждого способа образования поверхностей существует своя база для систематизации, например, в кинематическом способе образования поверхностей вполне естественно в основу систематизации положить вид образующей и закон ее перемещения.
По виду образующей различают
линейчатые (образующая-прямая) ,
циклические (образующая-окружность) , и другие поверхности,
по закону перемещения образующей –
поверхности вращения,
параллельного переноса,
винтовые и т. д.
При этом некоторые поверхности могут быть отнесены одновременно к различным классам, например, цилиндрическая поверхность вращения является линейчатой и поверхностью вращения. Поэтому разработка всевозможных систематизаций представляет собой сложную проблему.
В дальнейшем будем придерживаться принципа систематизации поверхностей, принятого в инженерной практике.
К 1 классу относятся не линейчатые поверхности, образующая которых li – кривая li. Ко 2 классу – линейчатые поверхности, образованные линией, т. е. li – прямая. Разделение поверхностей на подклассы показано в таблице.
А еще хорошая лекция ОБРАЗОВАНИЕ И ИЗОБРАЖЕНИЕ ПОВЕРХНОСТЕЙ
1. Классификация поверхностей. Задание поверхности на комплексном чертеже.
Поверхности разделяют:
По закону образования — на закономерные и незакономерные.
Закономерные задаются графически и аналитически, незакономерные — только графически.
По признаку развёртывания в плоскость — развёртывающиеся и неразвёртывающиеся.
По форме образующей:
— с прямолинейными образующими — линейчатые поверхности;
— с криволинейной образующей — кривые поверхности.
По способу перемещения образующей:
— с поступательным движением образующей;
— с вращательным движением образующей — поверхности вращения;
— с движением образующей по винтовой линии — винтовые поверхности.
Поверхности на комплексном чертеже могут быть заданы:
Проекциями направляющих и способом перемещения по ним образующих.
Семейством линий, принадлежащих поверхности — каркасный способ задания поверхности.
Очерком поверхности, т. е. линиями, ограничивающими на комплексном чертеже область существования проекций.
Источник