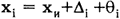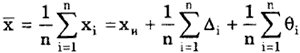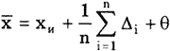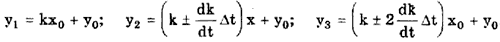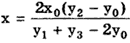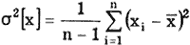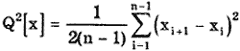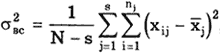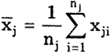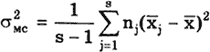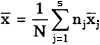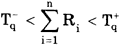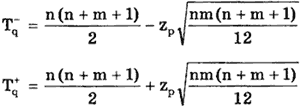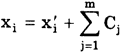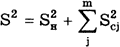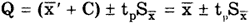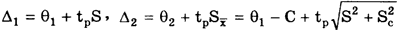Классификация погрешностей измерений способы устранения

Погрешности измерений и их классификация

Полученное из опыта значение измеряемой величины может отличаться от ее действительного (истинного) значения.

Погрешность измерения – отклонение результата измерения от истинного (действительного) значения измеряемой величины.

Это может быть обусловлено конструктивными недостатками прибора, несовершенством технологии его изготовления, а также влиянием различных внешних факторов.

Таким образом, погрешности классифицируют:

По источнику возникновения (метод, инструмент, субъект)

-Методические (зависят от метода измерения и способа включения приборов в электрическую цепь)

-Инструментальные (зависят от средства измерения)

-Субъективные (зависят от измерителя)

По условиям проведения измерений (температура, давление, влажность)

-Основные (измерения проводятся в нормальных условиях — при нормальной температуре, давлении, влажности)

-Дополнительные (условия отличны от нормальных)

По характеру проявления (систематические, случайные, промахи)

Систематические – погрешности, остающиеся постоянными или закономерно изменяющимися при повторных измерениях тем же способом и средствами. Т.е. они заранее известны и их легко исключить.

Случайные – погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Обычно выявляются в результате многократных измерений (не менее 10).

Промах – грубая ошибка, обусловленная неправильным отсчетом или расчетом, небрежностью измеряющего, поломки прибора, неправильно собранной схемы, невнимательности и т.д. Такие данные необходимо исключать.

По временному поведению измеряемой величины (статическая, динамическая)

Статическая – когда измеряемая величина не меняется за время измерения

Динамическая – когда прибор не успевает реагировать на изменения измеряемой величины.

По способу выражения измеряемой величины

Абсолютной погрешностью D Х называется разность между измеренным и действительным значениями.

– действительное значение измеряемой величины.

Выражается D Х в единицах измеряемой величины.

Относительная погрешность – отношение абсолютной погрешности к действительному значению измеряемой величины.

Выражается в процентах или относительных единицах. Относительная погрешность характеризует точность измерений.

Приведенная погрешность g _пр – отношение абсолютной погрешности к номинальному (нормированному) значению – верхнему пределу диапазона или поддиапазона измерения прибора.

Пределом измерения прибора называется наибольшая величина, на которую рассчитан данный прибор.

Прибор может иметь несколько пределов измерений (например, вольтметр).

Чем меньшую погрешность дает прибор, тем он точнее.

Выражается в процентах.

Максимальная приведенная погрешность определяет класс точности прибора.

Электроизмерительные приборы изготавливаются нескольких классов точности

Источник

Погрешности измерений и их классификация. Лекция

Погрешности измерений и их классификация .

При измерении физических величии с помощью даже самых точных и совершенных средств и методов их результат всегда отличается от истин­ного значения измеряемой физической величины, т.е. определяется с неко­торой погрешностью. Источниками погрешностей измерения являются сле­дующие причины: несовершенство используемых методов и средств измере­ний, нестабильность измеряемых физических величин, непостоянство климатических условий, внешние и внутренние помехи, а также различные субъек­тивные факторы экспериментатора.

Определение «погрешность» является одним из центральных в метрологии, в котором используются понятия «погрешность результата измере­ния» и «погрешность средства измерения».

Погрешностью результата измерения (погрешностью измерения) называется отклонение результата измерения от истинного значения измеряемой физической величины. Так как истинное значение измеряемой величины неизвестно, то при количественной оценке погрешности пользуются дейст­вительным значением физической величины.

Это значение находится экспериментальным путем и настолько близко к истинному значению, что для поставленной измерительной задачи может быть использовано вместо него.

Погрешность средства измерения (СИ) — разность между показаниями СИ и истинным (действительным) значением измеряемой физической величины. Она характеризует точность результатов измерений, проводимых дан­ным средством

Существует пять основных признаков , по которым классифицируются погрешности измерения.

По способу количественного выражения погрешности измерения делятся на абсолютные, относительные и приведенные.

Абсолютной погрешностью △ , выражаемой в единицах измеряемой величины, называется отклонение результата измерения х от истинного зна­чения х_н: (1.1)

и знак полученной погрешности, но не определяет качество самого проведенного измерения.

Понятие погрешности характеризует как бы несовершенство измере­ния. Характеристикой качества измерения является используемое в метроло­гии понятие точности измерений, отражающее меру близости результатов измерений к истинному значению измеряемой физической величины. Точ­ность и погрешность связаны обратной зависимостью. Иначе говоря, высо­кой точности измерений соответствует малая погрешность. Так, например, измерение силы тока в 10 А и 100 А может быть выполнено с идентичной аб­солютной погрешностью ∆ = ±1 А. Однако качество (точность) первого из­мерения ниже второго. Поэтому, чтобы иметь возможность сравнивать каче­ство измерений, введено понятие относительной погрешности.

Относительной погрешностью δ называется отношение абсолютной погрешности измерения к истинному значению измеряемой величины:

Мерой точности измерений служит величина, обратная модулю отно­сительной погрешности, т.е. 1/|δ|. Погрешность δ часто выражают в про­центах:

δ = 100 △ /х_н (%). Поскольку обычно △⋍ х_н, то относительная по­грешность может быть определена как δ ⋍ △ /х или δ = 100 △ /х (%).

Если измерение выполнено однократно и за абсолютную погрешность результата измерения △ принята разность между показанием прибора и ис­тинным значением измеряемой величины х_Н то из соотношения (1.2) следу­ет, что значение относительной погрешности δ уменьшается с ростом вели­чины х_н (здесь предполагается независимость △ от х_н ). Поэтому для изме­рений целесообразно выбирать такой прибор, показания которого были бы в последней части его шкалы (диапазона измерений), а для сравнения различ­ных приборов использовать понятие приведенной погрешности.

Приведенной погрешностью δ_пр, выражающей потенциальную точ­ность измерений, называется отношение абсолютной погрешности △ к неко­торому нормирующему значению X_N (например, к конечному значению шкалы прибора или сумме конечных значений шкал при двусторонней шка­ле).

По характеру (закономерности) изменения погрешности измерений подразделяются на систематические, случайные и грубые (промахи).

Систематические погрешности △ _с — составляющие погрешности из­мерений, остающиеся постоянными или закономерно изменяющиеся , при многократных (повторных) измерениях одной и той же величины в одних и тех же условиях. Такие погрешности могут быть выявлены путем детального анализа возможных их источников и уменьшены (применением более точных приборов, калибровкой приборов с помощью рабочих мер и пр.). Однако полностью их устранить нельзя.

По характеру изменения во времени систематические погрешности подразделяются на постоянные (сохраняющие величину и знак), прогресси­рующие (возрастающие или убывающие во времени), периодические, а также изменяющиеся во времени по сложному непериодическому закону. Основ­ные из этих погрешностей — прогрессирующие.

Прогрессирующая (дрейфовая) погрешность — это непредсказуемая по­грешность, медленно меняющаяся во времени. Прогрессирующие погрешно­сти характеризуются следующими особенностями:

• возможна их коррекция поправками только в данный момент времени, а далее эти погрешности вновь непредсказуемо изменяются;

• изменения прогрессирующих погрешностей во времени представляют со­бой нестационарный случайный процесс (характеристики которого изменяются во времени), и поэтому в рамках достаточно полно разработанной теории стационарных случайных процессов они могут быть описаны лишь с некоторыми ограничениями.

Случайные погрешности — составляющие погрешности измерений, изменяющиеся случайным образом при повторных (многократных) измере­ниях одной и той же величины в одних и тех же условиях. В появлении таких погрешностей нет каких-либо закономерностей, они проявляются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Практически случайные погрешности неизбежны, неустранимы и всегда имеют место в результатах измерений. Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики. В отличие от систематических случайные погрешности нельзя исклю­чить из результатов измерений путем введения поправки, однако их можно существенно уменьшить путем многократного измерения этой величины и последующей статистической обработкой полученных результатов.

Грубые погрешности (промахи) — погрешности, существенно превы­шающие ожидаемые при данных условиях измерения. Такие погрешности возникают из-за ошибок оператора или неучтенных внешних воздействий. Их выявляют при обработке результатов измерений и исключают из рас­смотрения, пользуясь определенными правилами.

По причинам возникновения погрешности измерения подразделяются на методические, инструментальные, внешние и субъективные.

Методические погрешности возникают обычно из-за несовершенства метода измерений, использования неверных теоретических предпосылок (допущений) при измерениях, а также из-за влияния выбранного средства изме­рения на измеряемые физические величины. При подключении электроизме­рительного прибора от источника сигнала потребляется некоторая мощность. Это приводит к искажению режима работы источника сигнала и вызывает погрешность метода измерения (методическую погрешность).

Так, например, если вольтметр обладает недостаточно высоким входным сопротивлением, то его подключение к исследуемой схеме способно из­менить в ней распределение токов и напряжений. При этом результат изме­рения может существенно отличаться от действительного. Для расчета мето­дической погрешности при измерении токов и напряжений необходимо знать внутренние сопротивления амперметров R_A и вольтметров R_v . Методическую погрешность можно уменьшить путем применения бо­лее точного метода измерения.

Инструментальные (аппаратурные, приборные) погрешности возни­кают из-за несовершенства средств измерения» т.е. из-за погрешностей средств измерений. Источниками инструментальных погрешностей могут быть, например, неточная градуировка прибора и смещение нуля, вариация показаний прибора в процессе эксплуатации и т.д. Уменьшают инструмен­тальные погрешности применением более точного прибора.

Внешняя погрешность — важная составляющая погрешности измере­ния, связанная с отклонением одной или нескольких влияющих величин от нормальных значений или выходом их за пределы нормальной области (на­пример, влияние влажности, температуры , внешних электрических и магнит­ных полей, нестабильности источников питания, механических воздействий и т.д.). В большинстве случаев внешние погрешности являются систематиче­скими и определяются дополнительными погрешностями применяемых средств измерений. .

Субъективные погрешности вызываются ошибками оператора при от­счете показаний средств измерения (погрешности от небрежности и невни­мания оператора, от параллакса, т.е. от неправильного направления взгляда при отсчете показаний стрелочного прибора и пр.). Подобные погрешности устраняются применением современных цифровых приборов или автомати­ческих методов измерения.

По характеру поведения измеряемой физической величины в процессе измерений различают статические и динамические погрешности.

Статические погрешности возникают при измерении установившего­ся значения измеряемой величины, т.е. когда эта величина перестает изме­няться во времени.

Динамические погрешности имеют место при динамических измерени­ях, когда измеряемая величина изменяется во времени и требуется установить закон ее изменения. Причина появления динамических погрешностей состо­ит в несоответствии скоростных (временных) характеристик прибора и ско­рости изменения измеряемой величины.

Средства измерений могут применяться в нормальных и рабочих усло­виях.

Эти условия для конкретных видов СИ ( средств измерения ) установлены в стандартах или технических условиях.

Нормальным условиям применения средств измерений должен удовлетворять ряд следующих (основных) требований:

температура окружающего воздуха (20±5) °С;

относительная влажность (65±15) %;

атмосферное давле­ние (100±4) кПа;

напряжение питающей сети (220±4) В и (115±2,5) В;

частота сети (50±1) Гц и (400±12) Гц.

Как следует из перечисленных требований, нормальные условия применения СИ характеризуются диапазоном значений влияющих на них величин типа климатических факторов и параметров элек­тропитания.

Рабочие условия применения СИ определяются диапазоном значений влияющих величин не только климатического характера и параметров электропитания, но и типа механических воздействий. В частности, диапазон климатических воздействий делится на ряд групп, охватывающих широкий диапазон изменения окружающей температуры.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

Способы обнаружения и устранения систематических погрешностей

Результаты наблюдений, полученные при наличии систематической погрешности, называются неисправленными. При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей.

Это может быть достигнуто следующими путями:

— устранением источников погрешностей до начала измерений. В большинстве областей измерений известны главные источники систематических погрешностей и разработаны методы, исключающие их возникновение или устраняющие их влияние на результат измерения. В связи с этим в практике измерений стараются устранить систематические погрешности не путем обработки экспериментальных данных, а применением СИ, реализующих соответствующие методы измерений;

— определением поправок и внесением их в результат измерения;

— оценкой границ неисключенных систематических погрешностей.

Постоянная систематическая погрешность не может быть найдена методами совместной обработки результатов измерений. Однако она не искажает ни показатели точности измерений, характеризующие случайную погрешность, ни результат нахождения переменной составляющей систематической погрешности. Действительно, результат одного измерения

где x_и — истинное значение измеряемой величины; _i — i-я случайная погрешность; _i — i-я систематическая погрешность. После устранения результатов многократных измерении получаем среднее арифметическое значение измеряемой величины

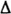
Если систематическая погрешность постоянна во всех измерениях, т.е. _i= ,то

Таким образом, постоянная систематическая погрешность не устраняется при многократных измерениях.

Постоянные систематические погрешности могут быть обнаружены лишь путем сравнения результатов измерений с другими, полученными с помощью более высокоточных методов и средств. Иногда эти погрешности могут быть устранены специальными приемами проведения процесса измерений. Эти методы рассмотрены ниже.

Наличие существенной переменной систематической погрешности искажает оценки характеристик случайной погрешности и аппроксимацию ее распределения. Поэтому она должна обязательно выявляться и исключаться из результатов измерений.

Для устранения постоянных систематических погрешностей применяют следующие методы:

— Метод замещения, представляющий собой разновидность метода сравнения, когда сравнение осуществляется заменой измеряемой величины известной величиной, причем так, что при этом в состоянии и действии всех используемых средств измерений не происходит никаких изменений. Этот метод дает наиболее полное решение задачи. Для его реализации необходимо иметь регулируемую меру, величина которой однородна измеряемой. Например, взвешивание по методу Борда, измерение сопротивления посредством моста постоянного тока и мер сопротивления.

— Метод противопоставления, являющийся разновидностью метода сравнения, при котором измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений. Например, способ взвешивания Гаусса.

— Метод компенсации погрешности по знаку (метод изменения знака систематической погрешности), предусматривающий измерение с двумя наблюдениями, выполняемыми так, чтобы постоянная систематическая погрешность входила в результат каждого из них с разными знаками.

— Метод рандомизации — наиболее универсальный способ исключения неизвестных постоянных систематических погрешностей. Суть его состоит в том, что одна и та же величина измеряется различными методами (приборами). Систематические погрешности каждого из них для всей совокупности являются разными случайными величинами. -Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются.

Для устранения переменных и монотонно изменяющихся систематических погрешностей применяют следующие приемы и методы.

— Анализ знаков неисправленных случайных погрешностей.

Если знаки неисправленных случайных погрешностей чередуются с какой-либо закономерностью, то наблюдается переменная систематическая погрешность. Если последовательность знаков «+» у случайных погрешностей сменяется последовательностью знаков «-» или наоборот, то присутствует монотонно изменяющаяся систематическая погрешность. Если группы знаков «+» и «-» у случайных погрешностей чередуются, то присутствует периодическая систематическая погрешность.

— Графический метод.

Он является одним из наиболее простых способов обнаружения переменной систематической погрешности в ряду результатов наблюдений и заключается в построении графика последовательности неисправленных значений результатов наблюдений. На графике через построенные точки проводят плавную кривую, которая выражает тенденцию результата измерения, если она существует. Если тенденция не прослеживается, то переменную систематическую погрешность считают практически отсутствующей.

— Метод симметричных наблюдений.

Рассмотрим сущность этого метода на примере измерительного преобразователя, передаточная функция которого имеет вид y = kx + y₀ , где х, у — входная и выходная величины преобразователя; k — коэффициент, погрешность которого изменяется во времени по линейному закону; у₀ — постоянная.
Для устранения систематической погрешности трижды измеряется выходная величина у через равные промежутки времени At. При первом и третьем измерениях на вход преобразователя подается сигнал х0 от образцовой меры. В результате измерений получается система уравнений:

Ее решение позволяет получить значение х, свободное от переменной систематической погрешности, обусловленной изменением коэффициента k:

Специальные статистические методы. К ним относятся способ последовательных разностей, дисперсионный анализ, и др. Рассмотрим подробнее некоторые из них.

Способ последовательных разностей (критерий Аббе).

Применяется для обнаружения изменяющейся во времени систематической погрешности и состоит в следующем. Дисперсию результатов наблюдений можно оценить двумя способами: обычным

и вычислением суммы квадратов последовательных (в порядке проведения измерений) разностей ( x_i+1 — x_i) 2

Если в процессе измерений происходило смещение центра группирования результатов наблюдений, т.е. имела место переменная систематическая погрешность, то 2 [x] дает преувеличенную оценку дисперсии результатов наблюдений. Это объясняется тем, что на 2 [x] влияют вариации . В то же время изменения центра группирования весьма мало сказываются на значениях последовательных разностей d _i = x _i+1-x _i, поэтому смещения почти не отразятся на значении Q 2 [x].

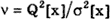
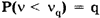
Отношение является критерием для обнаружения систематических смещений центра группирования результатов наблюдений. Критическая область для этого критерия (критерия Аббе) определяется как , где q = 1-Р — уровень значимости, Р — доверительная вероятность. Значения v_q для различных уровней значимости q и числа наблюдений n приведены в таблице. Если полученное значение критерия Аббе меньше при заданных q и n, то гипотеза о постоянстве центра группирования результатов наблюдений отвергается, т.е. обнаруживается переменная систематическая погрешность результатов измерений.

n	vq при q, равном	n	vq при q, равном
0.001	0.01	0.05	0.001	0.01	0.05
0.295	0.313	0.390	0.295	0.431	0.578
0.208	0.269	0.410	0.311	0.447	0.591
0.182	0.281	0.445	0.327	0.461	0.603
0.185	0.307	0.468	0.341	0.474	0.614
0.202	0.331	0.491	0.355	0.487	0.624
0.221	0.354	0.512	0.368	0.499	0.633
0.241	0.376	0.531	0.381	0.510	0.642
0.260	0.396	0.548	0.393	0.520	0.650
0.278	0.414	0.564

Дисперсионный анализ (критерий Фишера).

В практике измерений часто бывает необходимо выяснить наличие систематической погрешности результатов наблюдений, обусловленной влиянием какого-либо постоянно действующего фактора, или определить, вызывают ли изменения этого фактора систематическое смещение результатов измерений. В данном случае проводят многократные измерения, состоящие из достаточного числа серий, каждая из которых соответствует определенным (пусть неизвестным, но различным) значениям влияющего фактора. Влияющими факторами, по которым производится объединение результатов наблюдений по сериям, могут быть внешние условия (температура, давление и т.д.), временная последовательность проведения измерений и т.п.

После проведения N измерений их разбивают на s серий (s > 3) по n_j результатов наблюдений ( sn_j = N ) в каждой серии и затем устанавливают, имеется или отсутствует систематическое расхождение между результатами наблюдений в различных сериях. При этом должно быть установлено, что результаты в сериях распределены нормально. Рассеяние результатов наблюдений в пределах каждой серии отражает только случайные влияния, характеризует лишь случайные погрешности измерений в пределах этой серии. Характеристикой совокупности случайных внутрисерийных погрешностей будет средняя сумма дисперсий результатов наблюдений, вычисленных раздельно для каждой серии, т.е.

где x_ji — результат i-го измерения в j-й серии.
Внутрисерийная дисперсия 2 _BC характеризует случайные погрешности измерений, так как только случайные влияния обусловливают те различия (отклонения результатов наблюдений), на которых она основана. В то же время рассеяние _j различных серий обусловливается не только случайными погрешностями измерений, но и систематическими различиями (если они существуют) между результатами наблюдений, сгруппированными по сериям. Следовательно, усредненная межсерийная дисперсия

где , выражает силу действия фактора, вызывающего систематические различия между сериями.

Таким образом, 2 _BC /( 2 _BC + 2 _MC) характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайных погрешностей измерений, а 2 _MC /( 2 _BC + 2 _MC) — долю дисперсии, обусловленную межсерийными различиями результатов наблюдений. Первую из них называют коэффициентом ошибки, вторую — показателем дифференциации. Чем больше отношение показателя дифференциации к коэффициенту ошибки, тем сильнее действие фактора, по которому группировались серии, и тем больше систематическое различие между ними.

Критерием оценки наличия систематических погрешностей в данном случае является дисперсионный критерий Фишера F = 2 _MC 2 _BC. Критическая область для критерия Фишера соответствует P (F>F_q) = q.

Значения F_q для различных уровней значимости q, числа измерений N и числа серий s приведены в приложении 1, где k₂ = N-s , k₁ = s-1. Если полученное значение критерия Фишера больше F_q (при заданных q, N и s), то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.

Из всех рассмотренных способов обнаружения систематических погрешностей дисперсионный анализ является наиболее эффективным и достоверным, так как позволяет не только установить факт наличия погрешности, но и дает возможность проанализировать источники ее возникновения.

Если закон распределения результатов измерений неизвестен, то для обнаружения систематической погрешности применяют статистический критерий Вилкоксона.

Из двух групп результатов измерений x₁, x₂. x_n и y₁, y₂. y_m , n> = m> = 5 , составляется вариационный ряд, в котором все n + m значений x₁, x₂. x_n и y₁, y₂. y_m располагают в порядке их возрастания и приписывают им ранги — порядковые номера членов вариационного ряда. Различие средних значений каждого из рядов можно считать допустимым, если выполняется неравенство

где R_i — ранг (номер) члена x_i, равный его номеру в вариационном ряду T — _q и T + _q — нижнее и верхнее критические значения для выбранного уровня значимости q.

При mm>15 они рассчитываются по формулам:

где z_p — квантиль нормированной функции Лапласа.

Таблица. Критические значения T_q — и T_q + при q=0.05 и 0,01

n	m	q=0.05	q=0.01
Tq —	Tq +	Tq —	Tq +

Исключение систематических погрешностей путем введения поправок.

В ряде случаев систематические погрешности могут быть вычислены и исключены из результата измерения. Для этого используются поправки. Поправка C_j — величина, одноименная измеряемой, которая вводится в результат измерения x_i = x_i ‘ + _j + C_j с целью исключения составляющих систематической погрешности _j. При C_j = —_j j-я составляющая систематической погрешности полностью устраняется из результата измерения. Поправки определяются экспериментально или в результате специальных теоретических исследований. Они задаются в виде таблиц, графиков или формул.

Введением одной поправки устраняется влияние только одной составляющей систематической погрешности. Для устранения всех составляющих в результат измерения приходится вводить множество поправок. При этом вследствие ограниченной точности определения поправок случайные погрешности результата измерения накапливаются и его дисперсия увеличивается. Так как поправка известна с определенной точностью, то она характеризуется статистически — средним значением поправки С и СКО S_c. При исправлении результата x_i ‘ путем введения поправок C_j , где j = l, 2. m, по формуле

дисперсия исправленного результата

где S_н 2 — оценка дисперсии неисправленного результата; S_cj 2 — оценка дисперсии j-й поправки. Как видно, с одной стороны, уточняется результат измерения, а с другой — увеличивается разброс за счет роста дисперсии. Следовательно, необходимо найти оптимум.
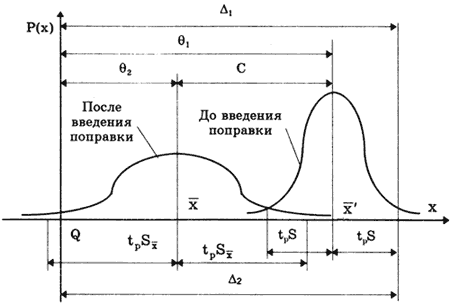
Пусть при измерении постоянной величины Q получено значение Q = ‘ t _pS ,где — оценка среднего арифметического неисправленного результата измерений; t_p — коэффициент Стьюдента.

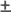
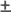
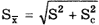
После введения поправки C t_pS_c результат измерения

где .
Максимальные доверительные значения погрешности результата измерения до и после введения поправки равны соответственно

Поправку имеет смысл вводить до тех пор, пока 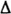₁ 0.5S_c 2 /S 2 . Из этого неравенства видно, что если оценка среднего квадратического отклонения поправки S_c стремится к нулю, то поправку имеет смысл вводить всегда. В практических расчетах погрешность результата обычно выражается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц младшего разряда, следующего за последним десятичным разрядом погрешности результата, все равно будет потеряна при округлении и вводить ее не имеет смысла.

Источник