Кинематика точки векторный способ описания движения материальной точки

1. Кинематика

1.1. Кинематика материальной точки. Описание движения материальной точки

Движение можно условно представить как последовательность положений, зафиксированных через бесконечно малые интервалы времени. Следовательно, описание движения есть описание всех этих последовательных положений, т.е. получение математического выражения, позволяющего вычислить конкретное положение материальной точки в любой момент времени.

Как положение, так и движение материальной точки, в данной системе отсчёта может быть описано различными способами.

1.1.1. Векторный способ

С помощью этого способа положение материальной точки определяется вектором, начинающимся в начале отсчёта и заканчивающимся там, где находится материальная точка.

Такие векторы принято называть радиус-векторами.

Начало отсчёта — это точка, связанная с телом отсчёта. Её выбирают так, чтобы было удобнее производить расчеты. Например, если необходимо узнать, какое расстояние пролетит камень, разумно в качестве начала отсчёта выбрать точку, в которой камень находился в момент броска.

Векторный способ описания движения предполагает получение уравнения r=r(t), гдеr— радиус-вектор, показывающий положение материальной точки в моментt, r(t) — выражение, позволяющее рассчитать мгновенное значениеr.

1.1.2. Координатный способ

Как уже отмечалось, положение любой точки в пространстве определяется совокупностью трёх величин  — координат. В декартовой системе координат это величиных,у, z.

Координаты и радиус-вектор связаны между собой: если начало отсчёта и начало координат совпадают, то координаты материальной точки в то же время есть проекции радиуса-вектора, определяющего её положение, на оси координат (см. рисунок). В аналитической форме эта связь имеет такой вид:

в данном выражении i,jиk — единичные векторы, направленные параллельно осямx,y иzсоответственно.

Координатный метод описания движения предполагает получение уравнений x=x(t), y=y(t) и т.д., гдех,у —мгновенные значения координат точки в моментt, x(t), y(t) — выражения, позволяющие рассчитать мгновенные значениях иу.

1.1.3. Естественный способ

Если известны траектория и направление движения материальной точки, удобно определять её положение естественным способом. Для этого используется скалярная величинаs(естественная координата). Это длина отрезка траектории от начала отсчёта О до материальной точки.

Естественный способ позволяет описать движение уравнением s=s(t), гдеs – естественная координата материальной точки к моментуt; s(t) — выражение, позволяющее рассчитать значениеsв моментt.

1.2. Характеристики движения

Для описания движения прежде всего необходима количественная мера изменения положения. Такой мерой является перемещение.

Перемещение — это вектор, соединяющий начальное и конечное положения материальной точки в пространстве и равный

В декартовых координатах перемещение можно выразить как

Перемещение за бесконечно малый интервал време­ни dt обозначаютdr. Направление этого вектора совпадает по направлению с касательной к траектории.

Имеет значение не только то, насколько далеко переместилась точка, но и то, как быстро произошло это перемещение. Поэтому необходима количественная мера быстроты изменения положения. Эта величина называется скоростью.

Средняя скорость равна отношению перемещения Δr, совершённого телом за время Δt, ко времени Δt

.

Например, автомобиль проехал по прямой дороге 60км за один час. Следовательно, его средняя скорость 60 км/час. Однако в процессе движения скорость, показываемая спидометром, в разные моменты времени будет разной, она может быть и больше — 60 км/час, и меньше. Объясняется это тем, что спидометр показывает не среднюю скорость, а мгновенную.

Мгновенная скорость равна пределу отношения перемещения dr ко времениdt, за которое произошло перемещение, приdt стремящемся к нулю:

.

Другими словами — мгновенная скорость — это векторная величина, равная производной от радиуса-вектора по времени. Вектор скорости направлен по вектору dr, т.е. вдоль касательной к траектории.

В декартовых координатах скорость выражается как

Мгновенную скорость можно выразить и так:

где v— модуль вектора мгновенной скорости,τ— единичный вектор, направленный по касательной к траектории.

Таким образом, вектор скорости равен произведению единичного вектора τ на модуль скорости.

Скорость может изменяться с течением времени. Поэтому необходима количественная мера быстроты изменения скорости. Такая характеристика называется ускорением.

Ускорение — это векторная величина, равная производной от скорости по времени,

.

Вектор ускорения направлен, как это видно из определения, по вектору dv, т.е. по вектору приращения скорости. Размерность ускорения [а]=м/с 2 . Используя естественный способ описания движения, можно записать

Из полученного выражения следует, что ускорение можно представить в виде суммы двух компонент.

Компонента представляет собой производную модуля скорости по времени, умноженную на единичный векторτ. Производная модуля скорости по времени показывает, как быстро он изменяется с течением времени. Следовательно, эта компонента ускорения показывает, как быстро изменяется модуль скорости. Направлена эта компонента по векторуτ, т.е. по касательной к траектории, и называетсятангенциальным ускорением а_τ.

Для того чтобы выяснить физический смысл компоненты , рассмотрим рисунок  . На нём изображён фрагмент траектории материальной точки.

Пусть траектория представляет собой дугу окружности радиусаR.

За время Δt материальная точка совершила перемещениеΔr. Пусть при этом скорость изменила только направление, а её модуль остался неизменным.

Переместим вектор конечной скорости v₂параллельно самому себе так, чтобы совместить начала векторов начальной и конечной скорости.

Треугольники, образованные векторами скоростиv₁v₂иΔv, радиусами дугиR и вектором перемещенияΔr, равнобедренные и имеют одинаковые углы при вершине.

Треугольник, образованный единичными векторами, имеет такой же угол при вершине, поскольку направления единичных векторов совпадают с направлениями векторов скоростей.

Считая угол α малым, можем записать . Из этого выражения получаем (здесь учтено, что модуль единичного вектораτ равенl). Разделим последнее выражение наΔt и перейдём к его пределу:

.

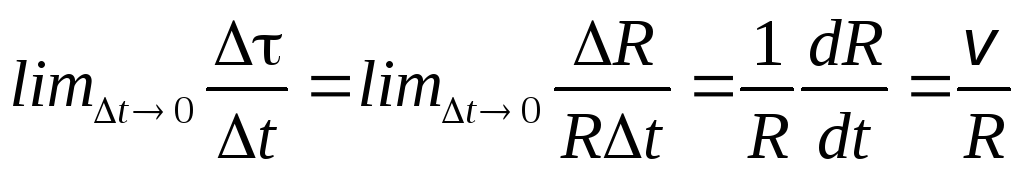
Таким образом, производная равна отношению модуля скорости к радиусу кривизны траектории. Направление производной совпадает с направлением вектораdτ, который, как видно из рисунка, при Δt0 и соответственно0 становится перпендикулярным к касательной к траектории.

Следовательно, компонента ускорения(здесьп — единичный вектор, перпендикулярный касательной к траектории). Эта компонента показывает, как быстро изменяется направление скорости, и называетсянормальным ускорением а_n, (его также называют центростремительным ускорением).

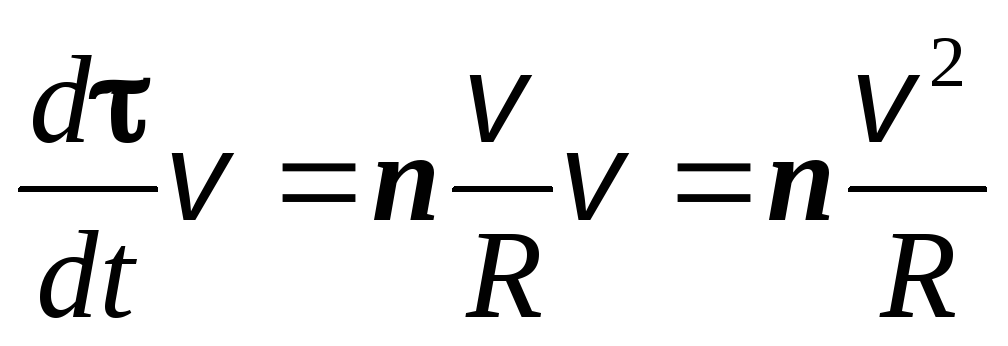
Окончательно выражение для ускорения тела, движущегося по криволинейной траектории, можно записать в виде

Модуль полного ускорения связан с модулями нормального и тангенциального ускорений так:

.

Источник

Кинематика точки векторный способ описания движения материальной точки

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Пусть точка М движется вдоль траектории АВ в системе отсчета Oxyz (рис.3). Выберем на траектории какую-нибудь неподвижную точку О 1 , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием S от точки О 1 . При движении точка М переместится в точку М 1 , соответственно изменится ее расстояние от точки О 1 . Таким образом, расстояние S зависит от времени, а характер этой зависимости позволит определить положение точки М на траектории в любой момент времени. Закон движения в этом случае имеет вид: s = s ( t ) .

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Источник