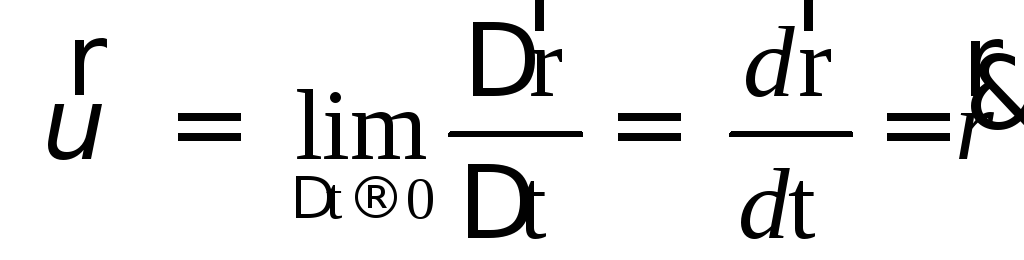Кинематика точки координатный способ задания движения точки

Координатный способ задания движения точки

Введение

Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.

Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):

Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.

Определение кинематических величин

Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .

Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.

Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .

Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .

Нормальное ускорение:
.
Вектор нормального ускорения:
; .
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.

Радиус кривизны траектории:
.
Центр кривизны траектории:
.

Единичный вектор в направлении бинормали:
.

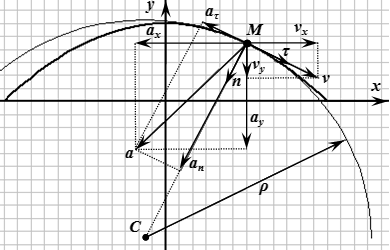
Пример решения задачи

Определение скорости и ускорения точки по заданным уравнениям ее движения

По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Уравнения движения точки:
, см;
, см.

Решение

Определение вида траектории

Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.

Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .

Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;

Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .

Строим параболу по точкам.

0	6
± 3	5,625
± 6	4,5
± 9	2,625
± 12	0

Определяем положение точки в момент времени .
;
.

Определение скорости точки

Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.

Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.

Определение ускорения точки

Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.

Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.

Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .

Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.

Радиус кривизны траектории:
.

Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .

Определение остальных величин

При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .

Определим остальные величины.

Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:

.
Вектор нормального ускорения:

.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:

.

Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:

.

Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020

Источник

1. Кинематика точки. Способы задания движения точки

Движение точки по отношению к избранной системе отсчёта считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени. В кинематике точки рассматриваются три основных способа описания движения точки: векторный, координатный и естественный.

1.1 Векторный способ задания движения точки

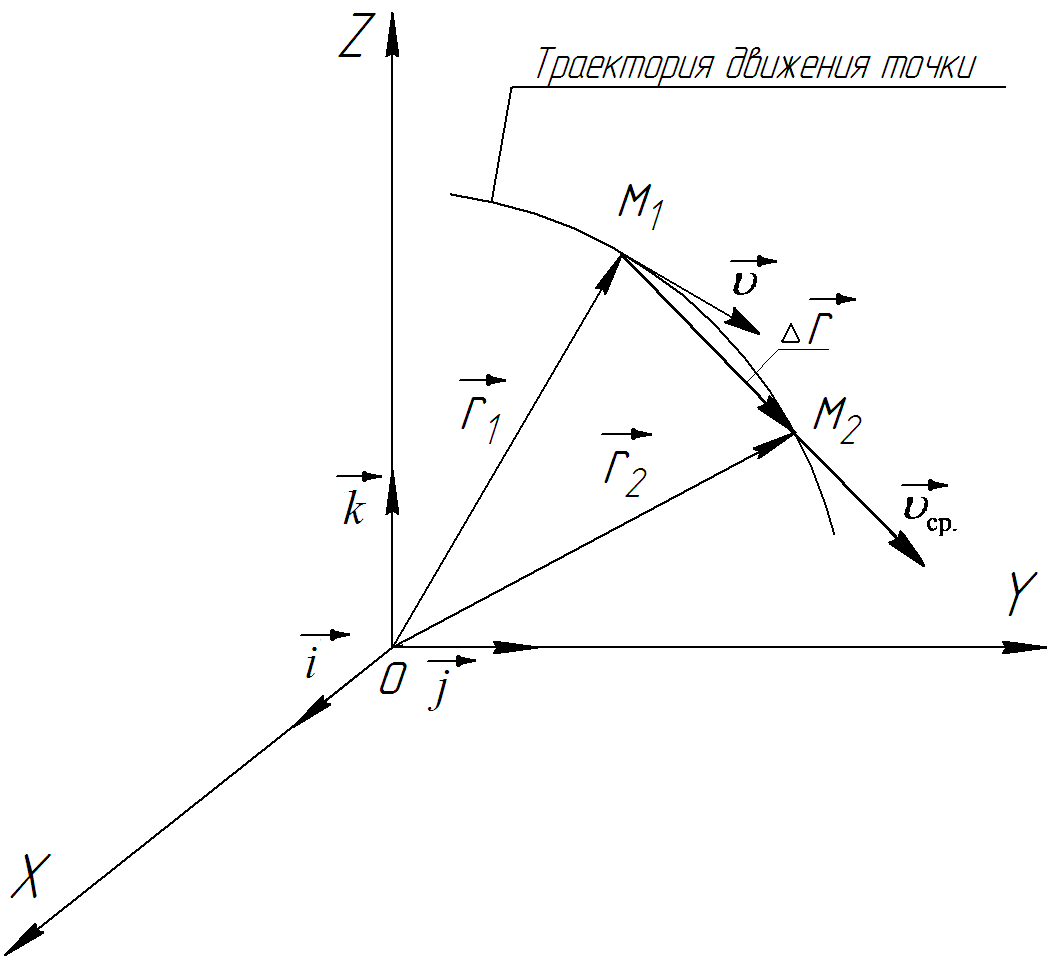
а) Положение точкив векторном способе задания движения определяется радиус-вектором , направленным из начала координат (от тела отсчёта) к данной точке (Рис.1).

Задать вектор как функцию времени – это значит уметь находить его модуль и направление в любой момент времени. При движении точки Мвекторбудет с течением времени изменяться и по модулю, и по направлению. Если каждому значению скалярного аргументаtпоставить в соответствие вектор, то называется векторной функцией скалярного аргумента, который описывает характер движения материальной точки. Это однозначная функция, потому что точкаМв каждое мгновение находится в каком-либо одном месте, она не может быть одновременно в нескольких местах.

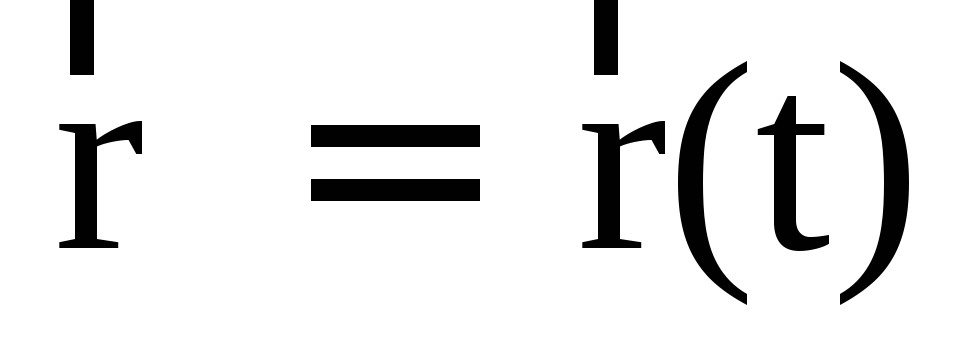
Равенство определяет собойзакон движенияматериальной точки в векторном виде и называетсявекторным уравнением движения материальной точки.

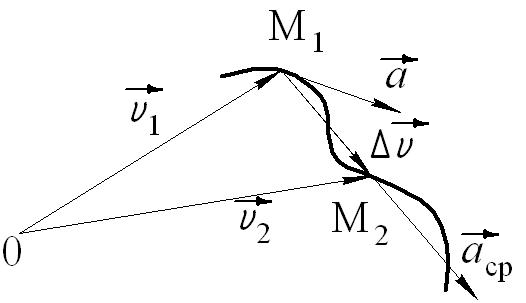
Годографом вектораназывается геометрическое место концов вектора в различные моменты времени, начало которых совмещены в одной фиксированной точке, то есть годограф – это кривая. Годографом радиус – вектора является траектория (Рис.1).

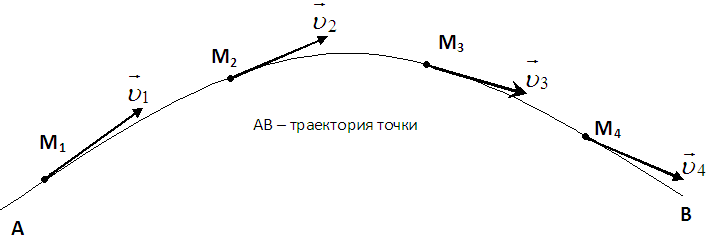
Траекториейназывается геометрическое место последовательных положений движущейся точки. Если в интервале времениt₁

Вектор средней скорости параллелен вектору перемещения

направлен в сторону движения точки, и не имеет точки приложения (Рис 3).

Очевидно, что чем меньше будет промежуток времени, для которого вычислена средняя скорость, тем величина будет точнее характеризовать движение точки. Для нахождения скорости точки в фиксированный момент времени уменьшим интервал Δtдо нуля и рассмотрим предел, к которому стремится средняя скорость. Этот предел и будет скоростью движущийся материальной точки в данный момент (мгновенной или истинной скоростью):

_{Производная по времени от функции обозначается точкой над символом этой функции, а вторая производная – двумя точками.}

Следовательно, при векторном способе задания движения точки скоростью называется первая производная радиус — вектора точки повремени.Скорость точки в этом случае характеризует быстроту изменения радиус – вектора с течением времени.

д) Направление скорости

При Δt→0 направление секущейМ₁М₂(Рис. 3) в пределе является направлением касательной. Поэтому:вектор скорости в данный момент времени направлен по касательной к годографу радиус – вектора в данной точке, т.е. по касательной к траектории точки (Рис.4).

При прямолинейном движении точки вектор скорости все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь по величине, а при криволинейном движении все время изменяется и направление вектора скорости точки (Рис.5). Единица измерения скорости в системе СИ — [м/с].

Годограф скорости – геометрическое место концов векторов скорости движущейся точки в последовательные моменты времени, начало которых совмещены в одной фиксированной точке.

е) Ускорение – вторая важнейшая характеристика движущейся точки. Только при прямолинейном движении точки ее скорость сохраняет свои численное значение и направление. При неравномерном криволинейном движении скорость точки изменяется и по модулю и по направлению.

Среднее ускорение точки– это отношение изменения скорости точки к тому промежутку времени, за которое оно произошло.Ускорение точки это векторная величина, которая характеризует быстроту изменения модуля и направления вектора скорости точки.

ё) Мгновенное ускорениеилиистинное ускорение точки – это предел, к которому стремится среднее ускорение при Δt→0, то есть:

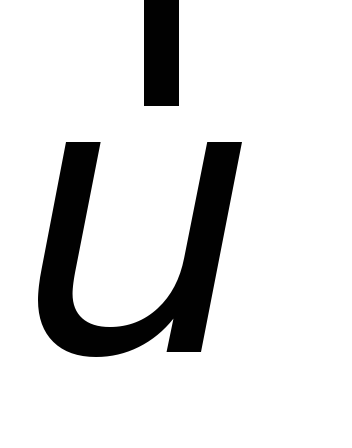
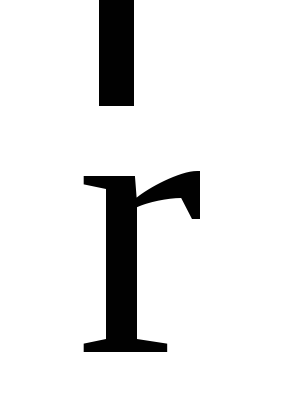
Ускорением называется первая производная по времени от вектора скорости или вторая производная по времени от радиус – вектора .

Размерность ускорения в системе СИ [м/с 2 ].

ж) Направление ускорения

Вектор среднего ускорения направлен по хорде (секущей) М₁М₂ годографа скорости (Рис.6).

При Δt→0, точкаМ₂стремится к точкеМ₁ и секущая в пределе превращается в касательную к годографу скорости, то естьвектор ускорения направлен по касательной к годографу скорости в данной точке (Рис.7).

При прямолинейном движении точки вектор ускорения направлен вдоль прямой, по которой движется точка.

Векторный способ описания движения применяют, как правило, при доказательстве теорем. При решении задач используют координатный и естественный способы задания движения точки.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник