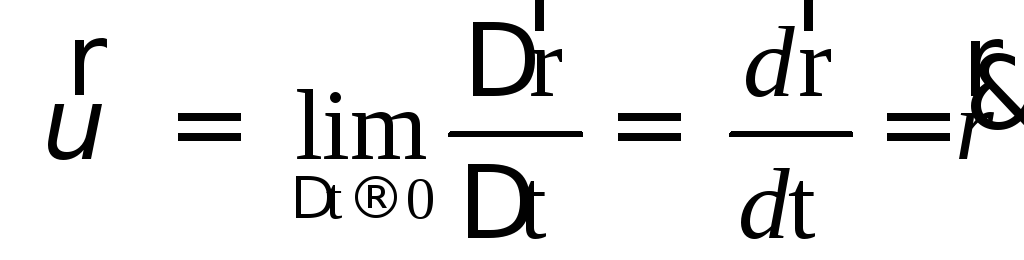Кинематика материальной точки способы задания движения материальной точки

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

1. Кинематика точки. Способы задания движения точки

Движение точки по отношению к избранной системе отсчёта считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени. В кинематике точки рассматриваются три основных способа описания движения точки: векторный, координатный и естественный.

1.1 Векторный способ задания движения точки

а) Положение точкив векторном способе задания движения определяется радиус-вектором , направленным из начала координат (от тела отсчёта) к данной точке (Рис.1).

Задать вектор как функцию времени – это значит уметь находить его модуль и направление в любой момент времени. При движении точки Мвекторбудет с течением времени изменяться и по модулю, и по направлению. Если каждому значению скалярного аргументаtпоставить в соответствие вектор, то называется векторной функцией скалярного аргумента, который описывает характер движения материальной точки. Это однозначная функция, потому что точкаМв каждое мгновение находится в каком-либо одном месте, она не может быть одновременно в нескольких местах.

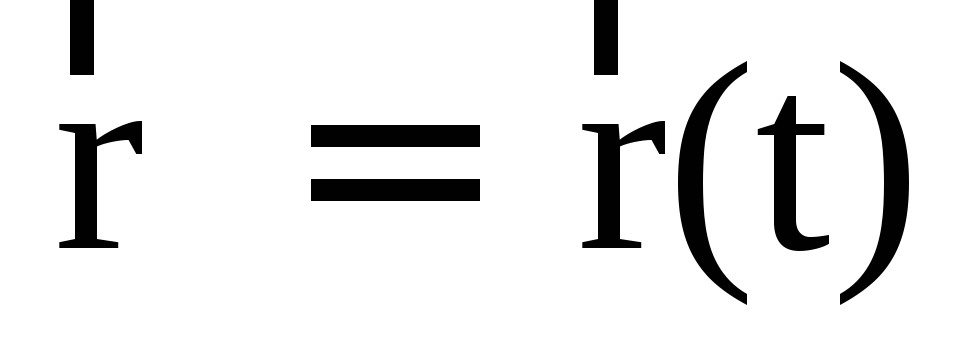
Равенство определяет собойзакон движенияматериальной точки в векторном виде и называетсявекторным уравнением движения материальной точки.

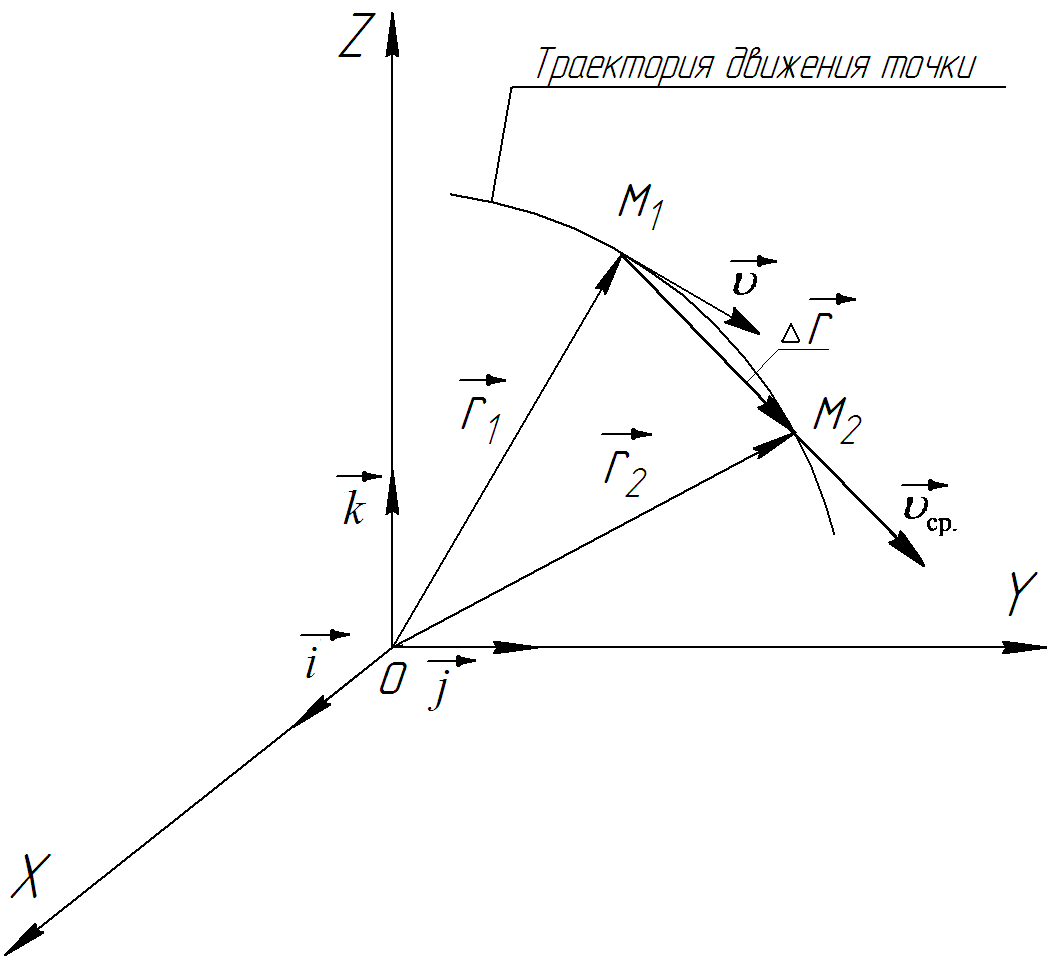
Годографом вектораназывается геометрическое место концов вектора в различные моменты времени, начало которых совмещены в одной фиксированной точке, то есть годограф – это кривая. Годографом радиус – вектора является траектория (Рис.1).

Траекториейназывается геометрическое место последовательных положений движущейся точки. Если в интервале времениt₁

Вектор средней скорости параллелен вектору перемещения

направлен в сторону движения точки, и не имеет точки приложения (Рис 3).

Очевидно, что чем меньше будет промежуток времени, для которого вычислена средняя скорость, тем величина будет точнее характеризовать движение точки. Для нахождения скорости точки в фиксированный момент времени уменьшим интервал Δtдо нуля и рассмотрим предел, к которому стремится средняя скорость. Этот предел и будет скоростью движущийся материальной точки в данный момент (мгновенной или истинной скоростью):

_{Производная по времени от функции обозначается точкой над символом этой функции, а вторая производная – двумя точками.}

Следовательно, при векторном способе задания движения точки скоростью называется первая производная радиус — вектора точки повремени.Скорость точки в этом случае характеризует быстроту изменения радиус – вектора с течением времени.

д) Направление скорости

При Δt→0 направление секущейМ₁М₂(Рис. 3) в пределе является направлением касательной. Поэтому:вектор скорости в данный момент времени направлен по касательной к годографу радиус – вектора в данной точке, т.е. по касательной к траектории точки (Рис.4).

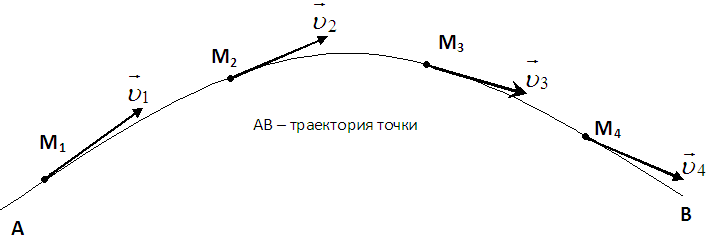
При прямолинейном движении точки вектор скорости все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь по величине, а при криволинейном движении все время изменяется и направление вектора скорости точки (Рис.5). Единица измерения скорости в системе СИ — [м/с].

Годограф скорости – геометрическое место концов векторов скорости движущейся точки в последовательные моменты времени, начало которых совмещены в одной фиксированной точке.

е) Ускорение – вторая важнейшая характеристика движущейся точки. Только при прямолинейном движении точки ее скорость сохраняет свои численное значение и направление. При неравномерном криволинейном движении скорость точки изменяется и по модулю и по направлению.

Среднее ускорение точки– это отношение изменения скорости точки к тому промежутку времени, за которое оно произошло.Ускорение точки это векторная величина, которая характеризует быстроту изменения модуля и направления вектора скорости точки.

ё) Мгновенное ускорениеилиистинное ускорение точки – это предел, к которому стремится среднее ускорение при Δt→0, то есть:

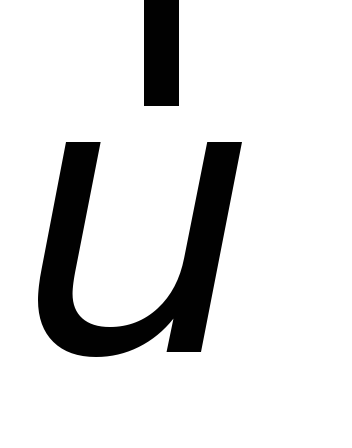
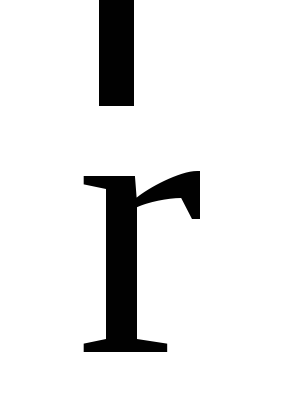
Ускорением называется первая производная по времени от вектора скорости или вторая производная по времени от радиус – вектора .

Размерность ускорения в системе СИ [м/с 2 ].

ж) Направление ускорения

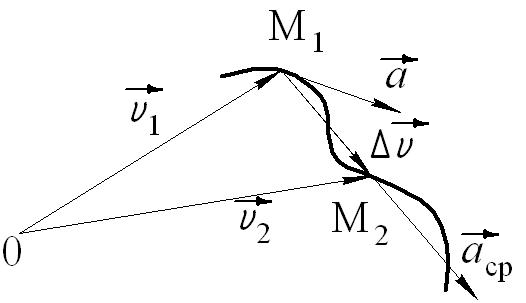
Вектор среднего ускорения направлен по хорде (секущей) М₁М₂ годографа скорости (Рис.6).

При Δt→0, точкаМ₂стремится к точкеМ₁ и секущая в пределе превращается в касательную к годографу скорости, то естьвектор ускорения направлен по касательной к годографу скорости в данной точке (Рис.7).

При прямолинейном движении точки вектор ускорения направлен вдоль прямой, по которой движется точка.

Векторный способ описания движения применяют, как правило, при доказательстве теорем. При решении задач используют координатный и естественный способы задания движения точки.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Кинематика

Кинематика – раздел механики, в котором изучаются движение материальных тел с геометрической точки зрения, без учета массы и действующих на них сил. Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный. Траектория точки – непрерывная кривая, которую описывает точка при своем движении.

Естественный сп . указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х= f(t).

Координатный сп . положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f₁(t), y=f₂(t), z=f₃(t).

Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t , получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоск-ти).

Векторный сп . положение точки определяется ее радиус-вектором , проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора. Связь между координатным и векторным способами: ,

( – орты – единичные вектора, сонаправленные с какой-либо осью)

модуль , направляющие косинусы: и т.д.

Переход от координатного способа к естественному: .

Скорость точки . Вектор ск-сти: – первая производная от радиус-вектора по времени (точка обозначает производную по времени); . Проекции скорости: , , . Модуль скорости:

, направляющие косинусы: и т.д. Если модуль скорости не изменяется с течением времени, то движение называется равномерным. При естественном сп.: – модуль скорости, вектор скорости: , – орт касательной, т.е. скорость всегда направлена по касательной к траектории. Если v>0, то движение происходит в сторону положительного отсчета дуговой координаты и наоборот. Движение в полярной системе координат: r=r(t) – полярный радиус, j = j ( t) – угол. Проекции скорости на радиальное направление , поперечное направление , модуль скорости ; x=rcos j , y=rsin j .

Ускорение точки . , [ м/сек 2 ]. Проекции уск.-я: и т.д. Модуль уск.-я: , направляющ. косинусы: , и т.д.

При задании движения в полярных координатах: проекции ускорения на радиальное направление , поперечное направление , модуль ускорения . При естественным сп. задания движения полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения: . Модуль нормального ускорения: , r – радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории ( ^ к касательной) всегда к центру кривизны, т.е. в сторону вогнутости. Нормальное ускорение характеризует изменение скорости по направлению. Модуль касательного ускорения , направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движ-ии направление касат. уск. и скорости совпадают, при замедленном – противоположно. ^ , Þ . Вектор ускорения лежит в соприкасающейся плоскости Þ его проекция на бинормаль равна 0 (главная нормаль лежит в соприкасающейся плоскости, т.е. в плоскости плоской кривой, бинормаль – ^ к главной нормали и касательной). Частные случаи движения точки : 1) Прямолинейное: радиус кривизны r = ¥ (бесконечно большой) Þ а _n =0, a=a _{t .} 2) Равномерное криволинейное движ-ие: v=const Þ a _t =0, a=a_n. Уск. появляется только за счет изменения направления скорости. Закон движ-ия: s=s₀+v × t, при s₀=0 v=s/t.

3) Равномерное прямолинейное движ-ие: а= a _t =a_n=0. Единственное движ-ие, где а=0.

4) Равнопеременное криволинейное движ-ие: a _t =const , v=v₀+a _t × t, . При равноуск. движении знаки у a _t и v одинаковы, при равнозамедленном – разные.

Простейшие движения твердого тела: поступательное и вращение вокруг неподвижной оси. Поступательное движение тела – такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельное самой себе. При поступат. движ. все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. Вращательное движение тела – такое движение твердого тела, при котором все точки, принадлежащие некоторой прямой, неизменно связанной с телом, остаются неподвижными. Эта прямая называется осью вращения тела. При этом движении все точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на оси вращения. Урав-ние (закон) вращательного движ.: j = f(t) – угол поворота тела в радианах. (1 рад= 180 о / p =57,3 о ).

Угловая ск-сть : , [ рад/с ] – определяет быстроту изменения угла поворота.

Вектор угловой скорости тела, совершающего вращение вокруг неподвижной оси, направлен вдоль оси вращения так, что если смотреть ему навстречу вращение будет против час. стрелке. » n»– число оборотов в мин. [об/мин], 1об=2 p рад, . Угловое ускорение тела: , [ рад/с 2 ]. Вектор углового ускорения также направлен вдоль оси вращения. При ускоренном движении совпадает по направлению с угловой скоростью и противоположно при замедленном вращении.

Частные случаи вращения тела: 1) Равномерное вращение: w = const, j = w t, w = j /t,

2) Равнопеременное вращение: w = w ₀ + e t; , здесь начальный угол j ₀ =0.

Скорости и ускорения точек вращающегося тела. – скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус–вектор этой точки. Модуль векторного произведения: v= w × r × sin( a )= w × (CM) , (СМ) – расстояние от точки М до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону вращения.

w _x , w _y , w _z – проекции вектора угловой скорости. Проекция вращательной (окружной) скорости: v_x= w _y z – w _z y; v_y= w _z x – w _x z; v_z= w _x y – w _y x. Если ось вращения совпадает с осью z, то v_x= – w y; v_y= w x. Ускорение : . Вращательное ускорение , модуль вращат. уск. а вр = e × r × sin a , направлено по касательной к траектории точки, т.е. параллельно скорости. Центростремительное (осестремительное) ускорение , а ц = w 2 × R, направлено по радиусу к оси (центру) вращения. Модуль полного уск.: . Угол, между векторами полного и центростремит-ного ускорений: .

Источник