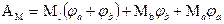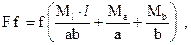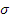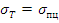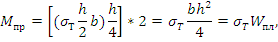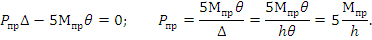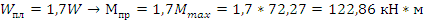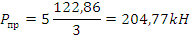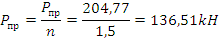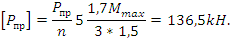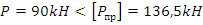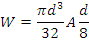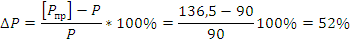О расчете конструкций по методу предельного равновесия
Этот метод разработан учеными во главе с профессором А. А. Гвоздевым и используется для расчета несущей способности статически неопределимых железобетонных конструкций. Использование этого метода приводит к экономическому эффекту за счет уменьшения количества арматуры, благодаря перераспределению усилий (изгибающих моментов) с учетом пластических деформаций бетона и арматуры.
В статически определимой свободно лежащей балке в стадии близкой к разрушению и достижению в арматуре предела текучести образуется участок с большими местными деформациями, называемый пластическим шарниром.
В балке, защемленной на опорах, с появлением пластического шарнира, повороту частей балки препятствуют лишние связи (защемление на опорах). Поэтому при дальнейшем увеличении нагрузки разрушение в пластическом шарнире не произойдет, пока не появятся новые пластические шарниры и выключатся лишние связи. В статически неопределимой системе возникновение пластического шарнира равносильно выключению лишней связи и снижению на одну степень статической неопределимости системы. Потеря геометрической неизменяемости системы может наступить лишь с образованием трех пластических шарниров – на обеих опорах и в пролете. Последовательность перераспределения изгибающих моментов под действием силы F0 можно рассмотреть на примере балки, защемленной на двух опорах (рис.23,а).
|
 |
Рис.23. Эпюры перераспределения изгибающих моментов в статически неопределимой балке
С появлением пластического шарнира на опоре B при нагрузке F0 балка как бы теряет одну связь и становится шарнирной на опоре B, но защемленной на опоре A (рис.23,б). Нагрузка увеличивается на Δ1F0, теряем одну связь на опоре A, и балка превращается в свободно опертую (рис.23, в). При дополнительной нагрузке Δ2F0 образуется пластический шарнир в пролете и балка разрушается. Полная нагрузка в балке составит 
.
Предельные расчетные моменты в пластических шарнирах равны M а – на опоре A; M b – на опоре B, M l – в пролете (рис.23, г). В предельном равновесии изгибающие моменты в балке можно найти статическим или кинематическим способом.
Пролетный момент: 
;
уравнение равновесия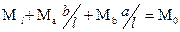 
;
где M0 – момент в статически определимой свободно лежащей балке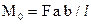 
.
Балку в предельном равновесии рассматривают как систему жестких звеньев, соединенных друг с другом в местах излома пластическими шарнирами (рис.23, д).
Если прогиб балки под силой F равен f, то углы поворота звеньев
; 
.
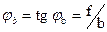
Исходим из равенства работ внешних и внутренних усилий 
.
Виртуальная работа силы F: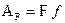 
.
Работа внутренних усилий (изгибающих моментов) в пластических шарнирах — равна сумме моментов на углы поворотов звеньев: 
.
Подставляем 
и 
;
;
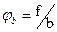
Уравнение виртуальных работ
отсюда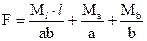 
— сила, при которой разрушится данная конструкция.
Если умножить правую и левую часть уравнения на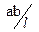 
, то получим уравнение равновесия такое же, как при расчете статическим способом.
Дата добавления: 2015-10-09 ; просмотров: 2207 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Кинематический способ метода предельного равновесия
Выбирая произвольное кинематически возможное состояние, мы можем получить по формуле (166.1) величину внешней нагрузки, которая представит собою некоторое приближение к истинной предельной нагрузке системы.
В отличие от статического метода, кинематический метод дает для определенной нагрузки завышенное значение, то есть оценку сверху.
Обозначим по-прежнему 
внешние силы и усилия в пластических элементах для истинного состояния, выберем произвольное кинематически возможное состояние, для которого обобщенные скорости деформации суть 
а скорости точек приложения внешних сил — 
. По заданному распределению 
с помощью условия пластичности находим усилия 
.
Поле скоростей v, q является кинематически возможным полем, поэтому мы можем применить принцип Лагранжа к истинному состоянию, приняв возможные перемещения пропорциональными скоростям 
. Таким образом, имеем:
(167.1)
Прибавим к правой части этого равенства и вычтем из нее 2 Получим
Но вследствие условия (163.1) последняя сумма в правой части положительна. Отсюда следует:
Если на систему действует только одна сила или если сравниваются системы сил, изменяющиеся пропорционально одному параметру, из полученного неравенства находим:
Таким образом, предельная нагрузка, найденная по кинематическому методу, всегда больше истинной. Знак равенства возможен только тогда, когда кинематический метод дает точное решение, то есть когда кинематически возможное состояние является в то же время статически возможным.
Источник
В чем заключается статический и кинематический способы расчета метода предельного равновесия?
Статический способ. Пролетный момент
Отсюда уравнение равновесия:
где M0=Fab/l — момент статически определимой свободно лежащей балки,
Из уравнения (11.5) следует, что сумма пролетного момента в сечении и долей опорных моментов, соответствующих этому сечению, равна моменту простой балки М0. Кроме того, из уравнения (11.5) вытекает, что несущая способность статически неопределимой конструкции не зависит от соотношения значений опорных и пролетного моментов и не зависит от последовательности образования пластических шарниров. Последовательность эта может быть назначена произвольно, необходимо лишь соблюдать уравнение равновесия. Однако изменение соотношения моментов в сечениях меняет значение нагрузки, вызывающей образование первого и последнего пластических шарниров, а также меняет ширину раскрытия трещин в первом пластическом шарнире.
Кинематический способ. Балку в предельном равновесии рассматривают как истему жестких звеньев, соединенных друг с другом в местах излома пластическими шарнирами (рис. 11.12, д). Если перемещение балки под действием силы F равно f, то углы поворота звеньев
Виртуальная работа силы F:
Виртуальная работа моментов:
а с учетом полученных выше значений:
Уравнение виртуальных работ:
Откуда расчетная предельная сила:
Если умножить левую и правую части уравнения (11.10) на ab/l, то получим найденное выше статическим способом уравнение равновесия (11.5).
9. В чем заключаются конструктивные требования по армированию статически неопределимой ж/б конструкции, отвечающие предпосылке расчета по методу предельного равновесия?
Чтобы обеспечить условия, отвечающие предпосылке метода предельного равновесия, т. е. возможности образования пластических шарниров и развитию достаточных местных деформаций при достижении конструкцией предельного равновесия, необходимо соблюдать следующие конструктивные требования:
· конструкцию следует запроектировать так, чтобы причиной ее разрушения не мог быть срез сжатой зоны или раздавливание бетона под действием главных сжимающих напряжений;
· армирование сечений, в которых намечено образование пластических шарниров, следует ограничивать так, чтобы относительная высота сжатой зоны ζ
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Источник
Метод предельного равновесия
Метод предельного равновесия называют так же методом разрушающих нагрузок, или методом расчета по несущей способности.
Условие прочности записывают в виде:
,
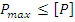
Где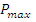 
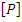
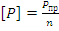
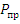
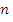
— наибольшая нагрузка, передаваемая на сооружение, а 
— допускаемая нагрузка, причем 
, где 
— предельная (разрушающая) нагрузка, 
— коэффициент запаса прочности.
Для определения разрушающей нагрузки используется диаграмма Прандаля, представляющая собой упрощенную зависимость между напряжением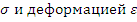 
. Так ведет себя упругопластичный материал.
σ 
| εT |
ε ε
Так как деформация на площадке текучести АВ в сотни раз превышает деформацию в упругой зоне ОА, то используют так же еще более простую диаграмму для жестко-пластичного материала. Считается, что материал не деформируется до предела текучести, а затем ведет себя как пластичный.
Рассмотрим процесс развития пластических деформаций по высоте сечения изгибаемой балки.
| М h |
| М |
| 1 2 |
| 1 2 |
y a)σmax
Выразим изгибающий момент через предел текучести для случаев б) и г) для балки прямоугольного сечения.
Случай б) – материал работает на границе упругой и пластической зон, когда в крайних волокнах наблюдается фибровая текучесть.
Где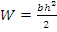 
— осевой момент сопротивления.
Случай г) – материал полностью находится в пластической зоне.
Где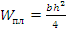 
— пластический момент сопротивления сечения.
Сравнивая, находим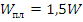 
, следовательно, предельный момент Мпр в полтора раза превышает упругий момент Мт, соответствующий фибровой текучести.
При возникновении во всех точках опасного сечения напряжений, равных пределу текучести, балка теряет несущую способность и становится геометрически изменяемой, так как ее части слева и справа от сечения могут поворачиваться друг относительно друга как при шарнирном сочленении. В таком случае говорят, что в сечении балки появился пластический шарнир.
Аналогично теряет несущую способность любая статически определимая рама.
Статически неопределимая конструкция (рама) может превращаться в механизм, если в ее сечениях появится n+1 пластический шарнир, где n – степень статической неопределимости. Решение задачи усложняется тем, что заранее трудно предугадать места появления пластических шарниров.
При расчете сооружений по методу предельного равновесия необходимо придерживаться такой последовательности:
1. Предварительно проводят обычный упругий расчет, что позволяет установить убывающий ряд степени напряженности стержней сооружения, используя эпюру изгибающих моментов.
2. Показывают геометрически изменяемый механизм сооружения, вводя (n+1) пластический шарнир в наиболее напряженные сечения опасных стержней убывающего ряда.
3. Загружают геометрически изменяемую систему, имеющую одну степень свободы, предельными моментами Мпр в пластических шарнирах и предельными внешними нагрузками Рпр в заданных сечениях или узлах.
4. Составляют уравнение равновесия мезанизма, пользуясь принципом возможных перемещений. Находят предельную нагрузку.
| 72,27 |
P=30 кН/м Рпр
| 21,46 |
P=ph=90kH 25,24 6 1 Рпр=3Рпр
| М |
h=3м θ
Рама нагружена распределенной нагрузкой P=30кН/м и сосредоточенной силой Р=90кН. Рама 5 раз статически неопределима, если решать методом сил, и 2 раза кинематически неопределима если решать методом перемещений. Раскрыв неопределимость, получаем эпюру М. Для получения механизма с одной степенью свободы необходимо поставить 5+1=6 шарниров. Пронумеруем сечения по степени убывания моментов. Загружаем механизм предельными моментами и предельными внешними нагрузками.
Принимаем в качестве возможного перемещения угол поворота вертикальных стержней θ. Так как ригель не перемещается по вертикали, т.е. в направлении действия распределенной нагрузки, то она не совершает работы. Точка приложения сосредоточенной силы переместится по горизонтали на величину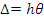 
. На этом перемещении сила совершает положительную работу Рпр∆; сечения 1-5 повернутся на угол θ, противоположный направлению моментов, следовательно, работа будет отрицательной.
Рассмотрим стержень круглого сечения. Для него
Чтобы получить допускаемую предельную нагрузку, разделим на коэффициент запаса прочности n=1,5:
Условие прочности выполняется, т.к. 
Экономия материала составит:
Момент сопротивления можно уменьшить на 52%.
Источник
