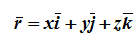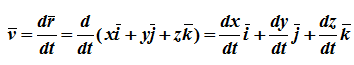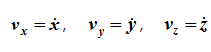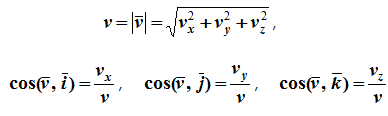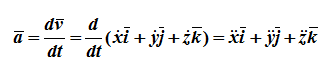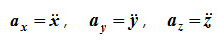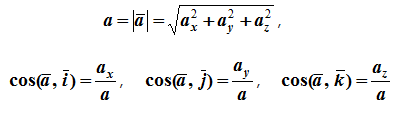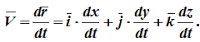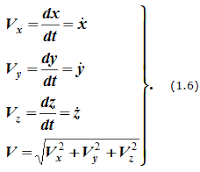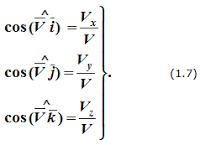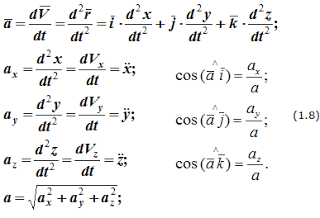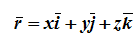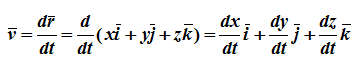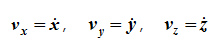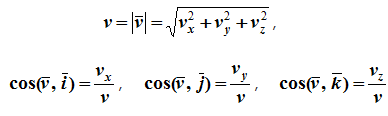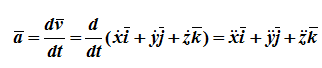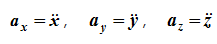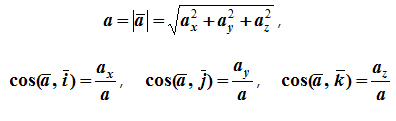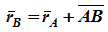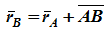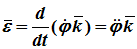Касательное ускорение точки при координатном способе задания движения

Координатный способ задания движения точки

Введение

Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.

Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):

Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.

Определение кинематических величин

Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .

Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.

Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .

Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .

Нормальное ускорение:
.
Вектор нормального ускорения:
; .
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.

Радиус кривизны траектории:
.
Центр кривизны траектории:
.

Единичный вектор в направлении бинормали:
.

Пример решения задачи

Определение скорости и ускорения точки по заданным уравнениям ее движения

По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Уравнения движения точки:
, см;
, см.

Решение

Определение вида траектории

Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.

Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .

Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;

Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .

Строим параболу по точкам.

0	6
± 3	5,625
± 6	4,5
± 9	2,625
± 12	0

Определяем положение точки в момент времени .
;
.

Определение скорости точки

Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.

Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.

Определение ускорения точки

Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.

Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.

Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .

Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.

Радиус кривизны траектории:
.

Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .

Определение остальных величин

При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .

Определим остальные величины.

Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:

.
Вектор нормального ускорения:

.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:

.

Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:

.

Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020

Источник

iSopromat.ru

Рассмотрим определение скорости и ускорения точек при координатном способе задания движения, а также, модуль и направление скоростей и ускорений и их проекции на оси координат:

Проекции скорости на оси координат равны производным соответствующих координат по времени:

Модуль и направление скорости определяются выражениями

Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени

Модуль и направление ускорения определяются выражениями

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

При координатном способе задания движения точки в выбранной системе координат задаются координаты движущейся точки как функции от времени.

В прямоугольной декартовой системе координат это будут уравнения:

Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.

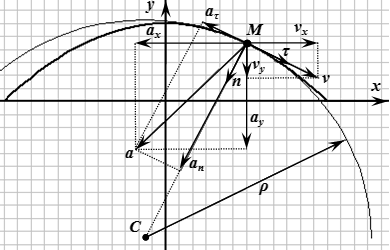
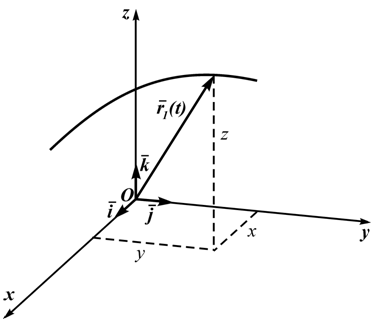
Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):

Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:

Направление вектора скорости определяется с помощью направляющих косинусов:

Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.

Аналогичны формулы для определения ускорения точки:

Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

1.4 Определение скорости и ускорения точки при координатном способе задания движения

Связь векторного способа задания движения и координатного дается соотношением

Из определения скорости

Проекции скорости на оси координат равны производным соответствующих координат по времени:

Модуль и направление скорости определяются выражениями

Из определения ускорения

Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени

Модуль и направление ускорения определяются выражениями

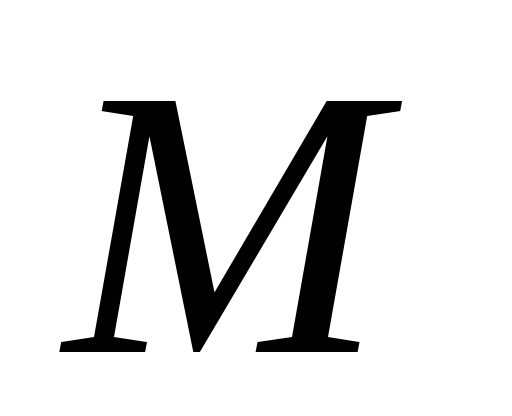
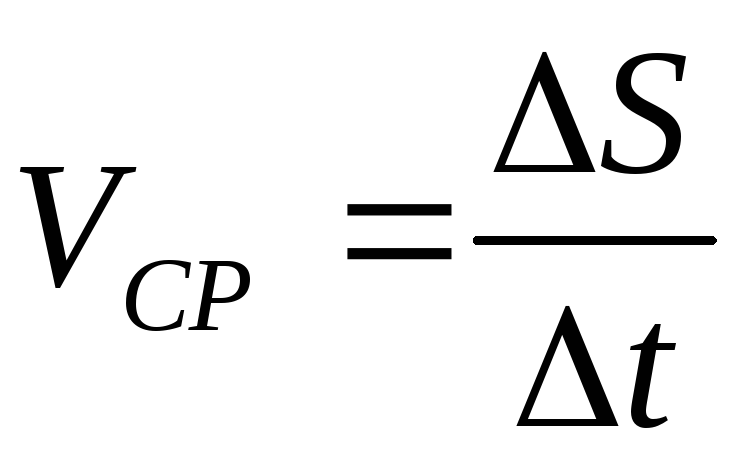
42 Определение скорости и ускорения точки при естественном способе задания движения Скорость точки.Вектор скорости точки всегда направлен по касательной вдоль оси , но может не совпадать с ней по направлению. За время t точка переместилась из М в М1 (ММ1=S) Скорость точки за этот промежуток времени равна: Скорость точки в данный момент времени равна:

числовая величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) точки по времени. Направлен вектор скорости по касательной к траектории, которая нам наперед известна. Если величина, то вектор скоростинаправлен в положительном направлении отсчета расстояния, а если, то в отрицательном.

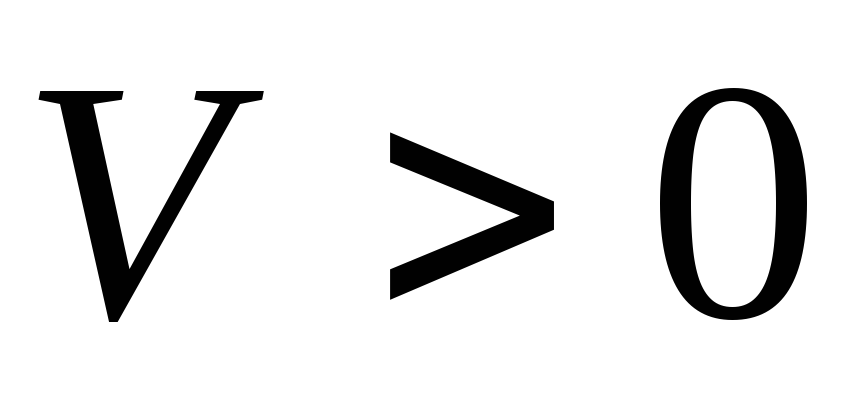
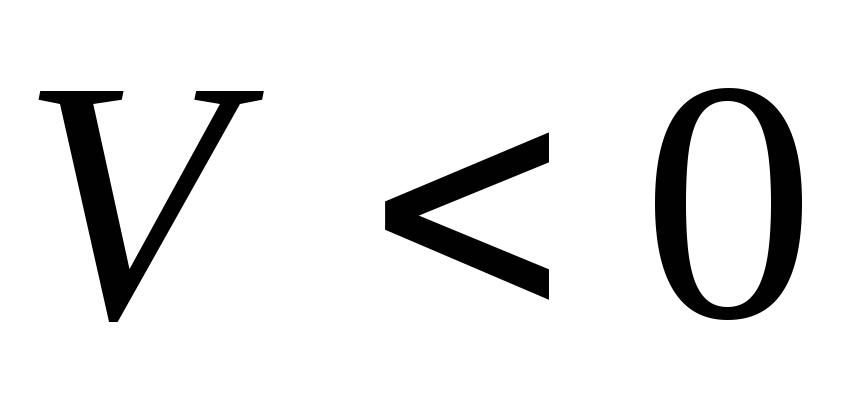
Следовательно, численная величина скорости определяет одновременно и модуль вектора скорости и сторону, в которую он направлен.

Касательное и нормальное ускорения точки.

При естественном способе задания движения вектор ускорения определяют по его проекции на оси nb, имеющие начало в точке и движущиеся вместе с нею. Эти оси, называем осями естественного трехгранника, направлены следующим образом: ось — вдоль касательной к траектории в сторону положительного отсчета расстояния s; ось по нормали, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось— перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль, лежащая в соприкасающейся плоскости (в плоскости самой кривой, если кривая плоская), называется главной нормалью, а перпендикулярная к ней нормаль— бинормалью.

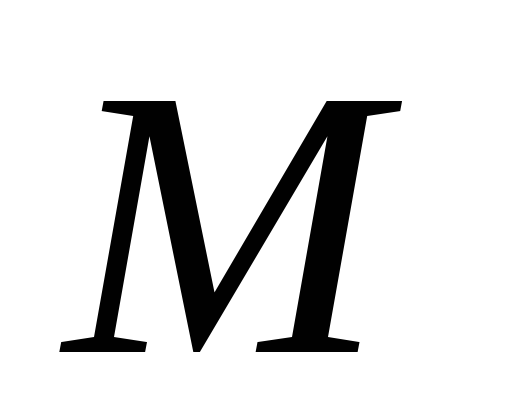
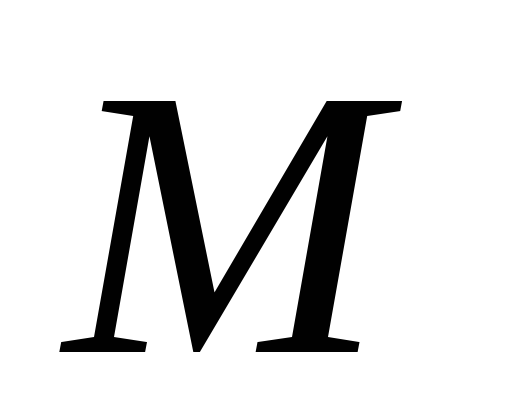
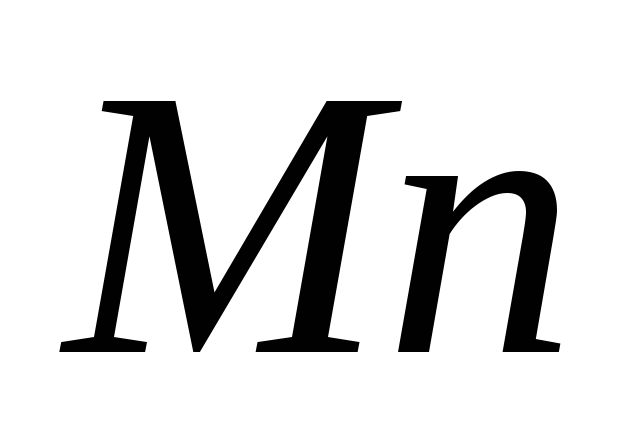
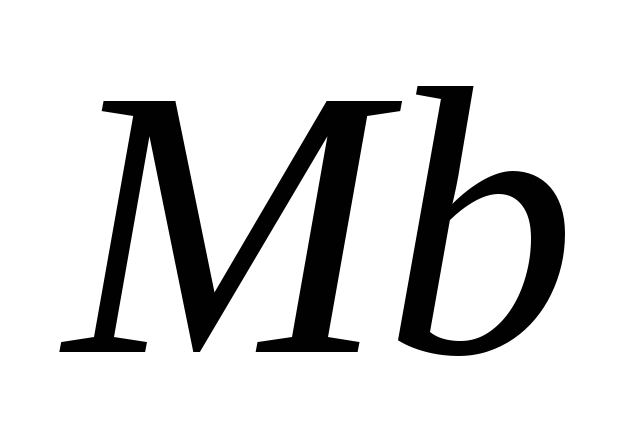
Проекции ускорения на оси  и Мn

, ,

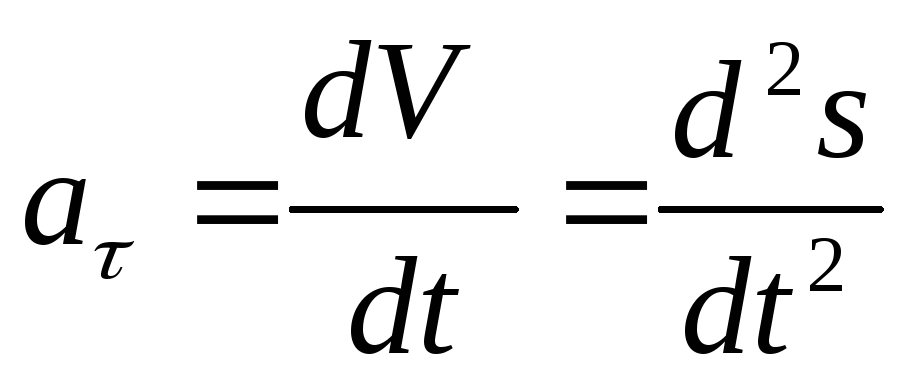
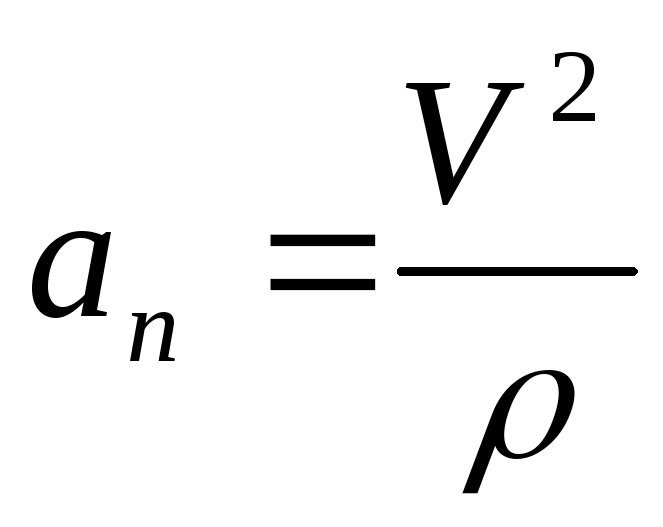
где  — радиус кривизны траектории.

Проекция ускорения точки на касательную равна первой производной от численной величины скорости или второй производной от расстояния (криволинейной координаты) по времени, а проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю().

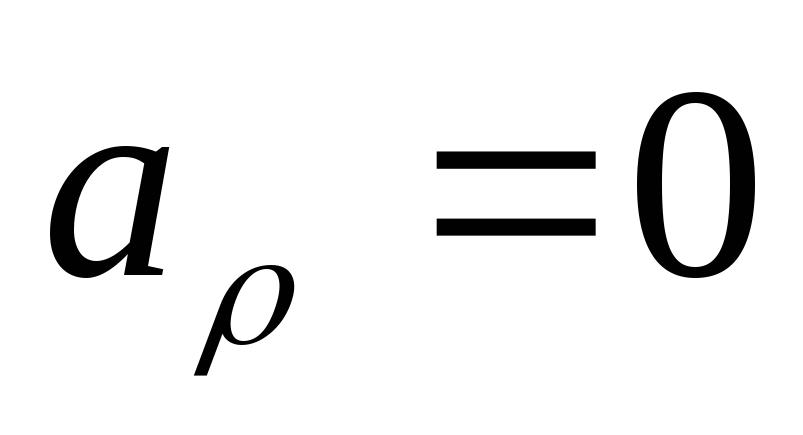
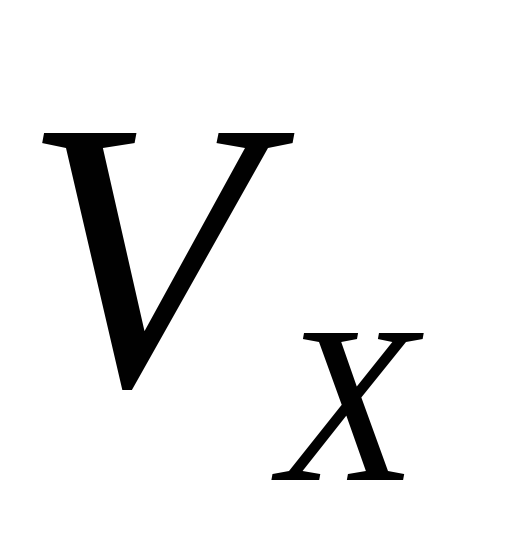
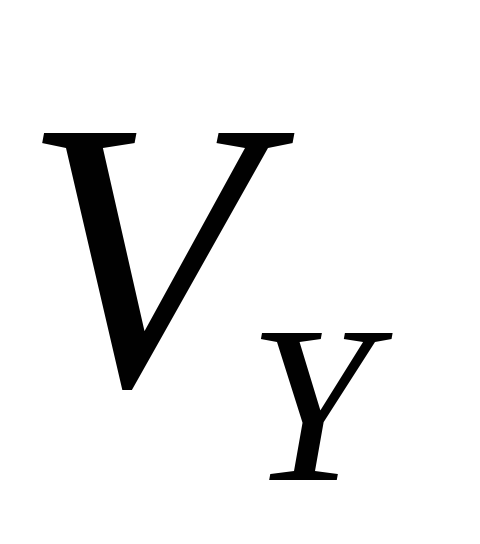
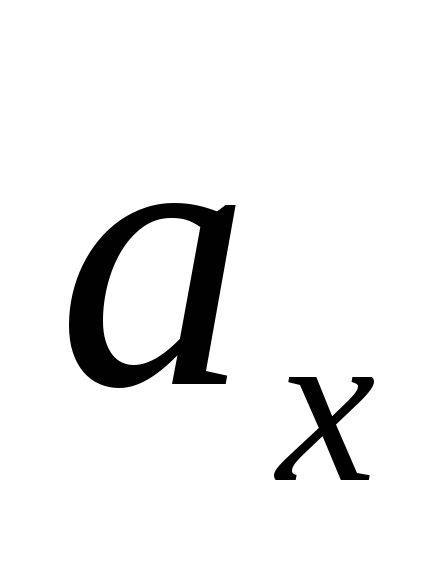
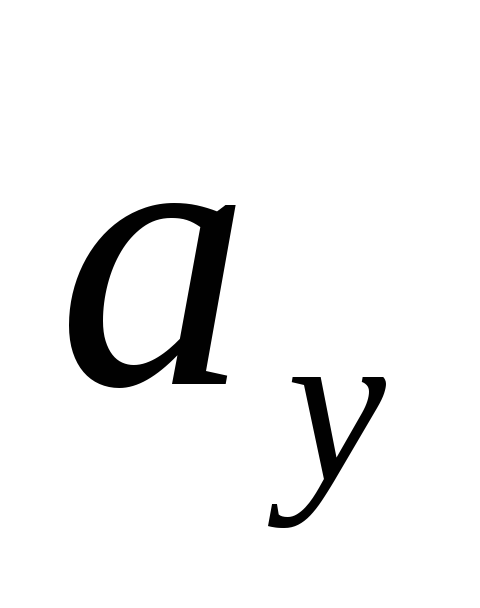
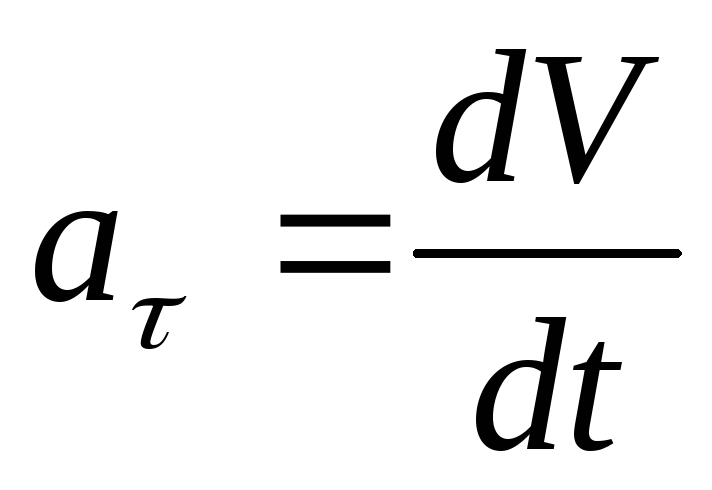
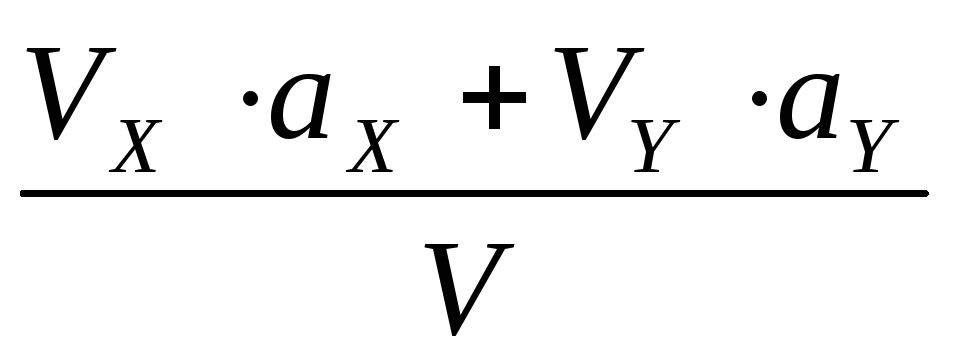
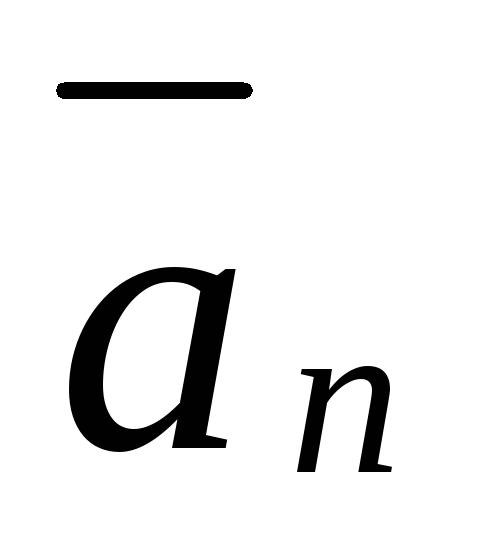
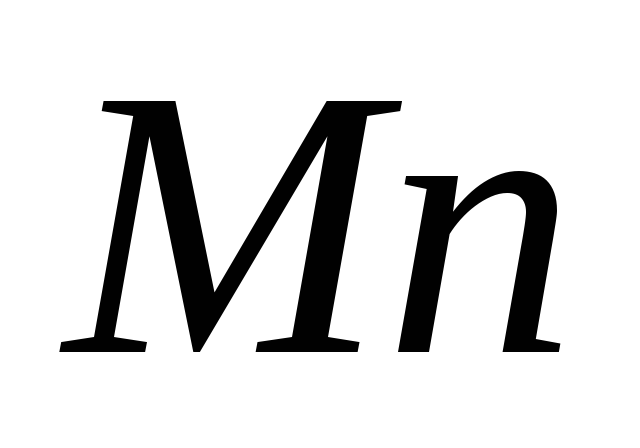
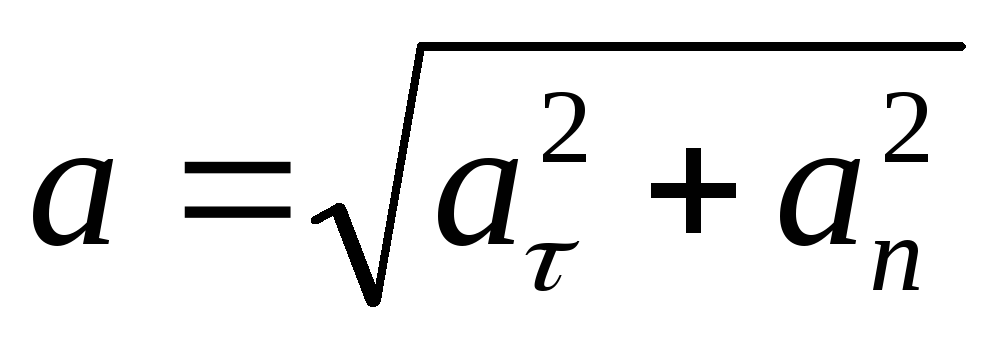
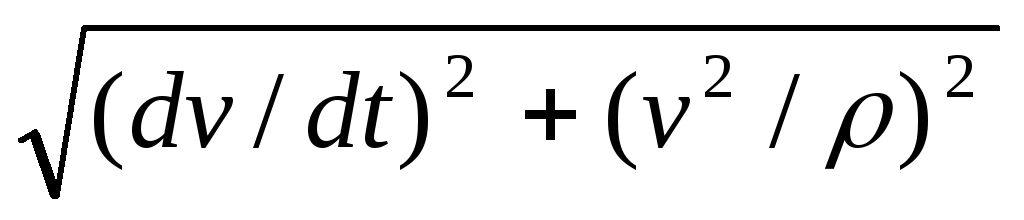
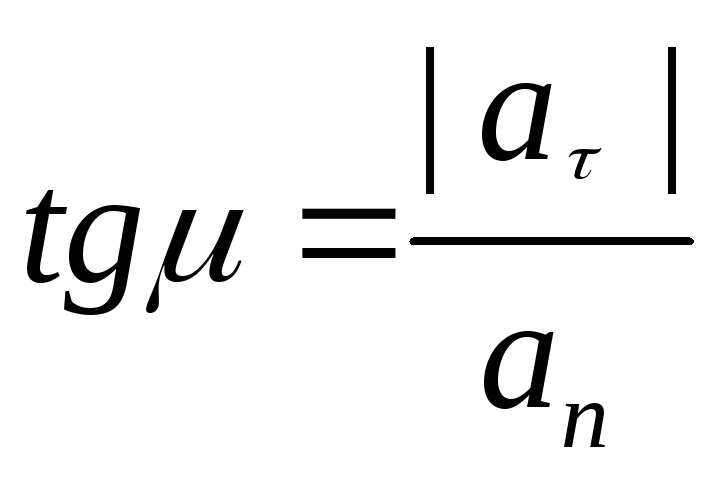
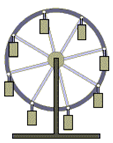
Если заданы проекции скорости и, а так же проекции ускоренияив данный момент времени, то величину касательного ускорения точки можно определить по формуле:

= .

Вектор ускорения точки изображается диагональю параллелограмма, построенного на составляющих и n (=+n).Так как эти составляющие взаимно перпендикулярны, то модуль вектора а и угол его отклонения от нормали определяется формулами:

=,.

43 кинемотика твердого тела .виды движения твердых тел.поступательное движения твердого тела. во многих случаях деформации твердых тел столь незначительны, что ими можно пренебречь при исследовании движения и равновесия твердых тел и рассматривать эти тела как недеформируемые (или абсолютно твердые)Абсолютно твердым телом называют такое твердое тело, расстояние между двумя любыми точками которого остается неизменным. Теоретическая механика изучает движение и равновесие только абсолютно твердых тел, и для краткости их называют просто твердыми телами .Задачи кинематики твердого тела разделяются на 2 части:1. Задачи движения и изучения кинематических характеристик движения всего тела в целом.2. Изучение движения каждой из точек тела в отдельности.Твердое тело может совершать пять видов движения: поступательное, вращение вокруг неподвижной оси, плоскопараллельное, вращение вокруг неподвижной точки и свободное.Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д.

Рис. 1.1

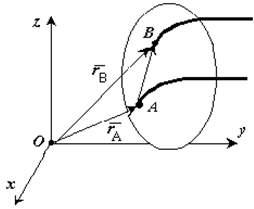
Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.Доказательство. Если выбрать две точки твердого тела А и В (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением

Траектория точки А – это кривая, которая задается функцией r_A(t), а траектория точкиB – это кривая, которая задается функцией r_B(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.Продифференцируем по времени выражение

Рис. 1.2

Продифференцируем по времени скорость и получим выражение a_B = a_A. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.

Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

44 Вращательное движение ТВЕРДОГО ТЕЛА угловая скорость угловое ускорения Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки,называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П , одна из которых неподвижна, а другая жестко связана с телом. φ=φ(t) – уравнение вращательного движения твердого тела.

Рис. 1.3 За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

где k – единичный вектор оси вращения.

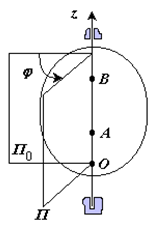
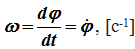
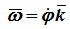
Угловое ускорение – мера изменения угловой скорости:

Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)

Рис. 1.4

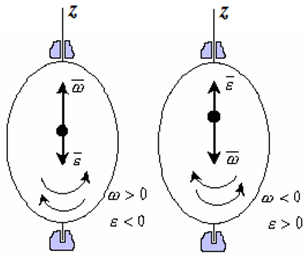
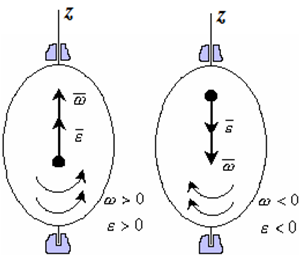
Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.При ε 0, то имеем замедленное вращение в положительную сторону. Векторыω и ε направлены в противоположные стороны.Если ε >0 при ω 13 / 25 13 14 15 16 17 18 19 20 21 > Следующая > >>

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник