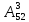- 52 карты раздаются 4-м игрокам, каждому по 13 карт. Сколькими способами их можно раздать, если
- Лучший ответ
- 20 Футбольных команд, среди которых 4 призёра предыдущего первенства, по жеребьевке разбиваются на 4 занумерованные подгруппы по 5 команд.
- Решение:
- 52 Карты раздаются четырём игрокам (каждому по 13 карт)
- Решение:
- 4) Картошки, 5) наполеон, 6) невские.
- Решение:
- §3 Задачи для самостоятельного решения.
52 карты раздаются 4-м игрокам, каждому по 13 карт. Сколькими способами их можно раздать, если

| Posted Февраль 19, 2014 by Полинский Артем Владиславович |
| Категория: Комбинаторика |
| Всего просмотров: 19257 |
| 52 карты раздаются 4-м игрокам, каждому по 13 карт. 1. Каждый игрок получит туза; Лучший ответ52 карты раздаются 4-м игрокам, каждому по 13 карт. Сколькими способами их можно раздать, если 1. Каждый игрок получит туза; 1. Каждый игрок получит туза; Правило произведения. Если объект A можно выбрать из множества объектов m способами и после каждого такого выбора объект B можно выбрать \(n\) способами, то пара объектов (A,B) в указанном порядке может быть выбрана \( m*n\) способами. Получаем \(n\) способов $$n = n_0*n_1*n_2*n_3*n_4 => $$$$n = 4* \frac<48!><12!36!>*\frac<36!><12!24!>*\frac<24!><12!12!>*1 = $$$$ = 4* \frac<48!> <12!12!12!12!>\approx 9.43 × 10^ <26>$$ Число перестановок c повторениями (k различных элементов, где элементы могут повторяться \(m_1, m_2, …, m_k\) раз и \(m_1 + m_2 +… + m_k = n\), где n — общее количество элементов) вычисляется по формуле: $$P(m_1,m_2. m_k) = \frac 2. Один из игроков получит все 13 карт единой масти. Для ответа на вопрос «сколькими способами можно раздать 52 карты 4-м игрокам по 13, при этом один из игроков получит 13 карт одной масти» применим правило произведения, получаем \(n\) способов $$n = n_1*n_2*n_3*n_4 => $$$$n = 4*\frac<39!><13!26!>*\frac<26!><13!13!>*1 = $$$$ = 4*\frac<39!> <13!13!13!>= 3.38 × 10^ <17>$$ Способ 2. 3. Все тузы попадут к одному из игроков. Для ответа на вопрос «сколькими способами можно раздать 52 карты 4-м игрокам по 13, при этом все тузы попадут одному игроку» применим правило произведения, получаем \(n\) способами $$n = n_1*n_2*n_3*n_4 => $$$$n = 1*\frac<48!><9!39!>*\frac<39!><13!26!>* \frac<26!> <13!13!>*1 = $$$$ = 1*\frac<48!> <9!13!13!13!>\approx 1.42 × 10^ <26>$$ Способ 2. 4. 2 определенных игрока не получат ни одного туза Способ 2. Источник 20 Футбольных команд, среди которых 4 призёра предыдущего первенства, по жеребьевке разбиваются на 4 занумерованные подгруппы по 5 команд.Найти вероятности события: Решение:n(Ω) = Т.к. точно по одному призёру в каждой группе, то распределяем 16 команд по 4-м подгруппам, а затем учтём число перестановок призёрных команд n(A)=4! p(A)= 52 Карты раздаются четырём игрокам (каждому по 13 карт)Найти вероятности следующих событий: Решение:Опыт: раздача 52 карт между 4-ми игроками поровну. n(Ω)= n(A) = ( (1-й игрок) (2-й игрок) (3-й игрок) Упростим: n(Ω) = n(A)= p(A)= 2) n(B)=С 1 4 · С 1 4 · С 13 39 · С 13 26 · С 13 13 ≤1 выбор выбор 2-ой 3-й 4-й масти игрока игрок игрок игрок Р(В)= 3) n(C)= С 1 4 · С 4 4 · С 9 48 · С 13 39 · С 13 26 · С 13 13 =1 выбор 1-ый 2-ой 3-й 4-й игрока игрока игрок игрок игро P(C)= 4) ) n(D)=С 13 48 · С 13 35 · С 13 (22+4) · С 13 13 =1 1-й без 2-ой без 3-й с 4-й с тузов тузов тузами n(D)= P(D)= В магазине имеется шесть сортов пирожных:1) эклеры, 2) буше,3) корзиночки, 4) Картошки, 5) наполеон, 6) невские.1. Сколько различных наборов из 10 пирожных можно получить? 2. Найти вероятность события: Решение:Элементарные исходы — это сочетания с повторениями. n(Ω)= n()= (вычисления проводим на калькуляторе) 2. n( P( §3 Задачи для самостоятельного решения.Команда участников КВН состоит из 8 студентов. При этом: 4 студента I курса, 2 студента II курса, 1 студент III курса и 1 студент IV курса. Для участия в конкурсе случайно выбирают четырех человек. Найти вероятности следующих событий: 1) А= <все учатся на разных курсах >, Ответ:1) Р(А)= 4/35; 2) Р(В)=3/14; 3) Р(С)=69/70 Шесть студентов случайным образом выстроились в буфете в очередь. Найти вероятности событий:1) А= Ответ:1) Р(А)=1/30; 2) Р(В)=1/3 Случайным образом набирают шестизначный код сейфа. Найти вероятности событий : Ответ:1)Р(А)=10 -6 ; 2)Р(В)=1/151200; 3) Р(С)=1/4096 В тесте 5 заданий и 4 варианта ответов (1 верный). Студент случайным образом выбирает ответы. Найти вероятности событий: Ответ:1) Р(А)=1/1024;2) Р(В)=27/1024;3) Р(С)=243/1024; 4) Р( D)=781/1024 Для подготовки к экзамену студент получил 5 вопросов по теме I, 3 вопроса по теме II, 2 вопроса по теме III и 1 вопрос по теме IV.Все вопросы по теме I студент знал на «отлично», вопросы темы II на «хорошо», вопросы темы III на «удовлетворительно», а тему IV не успел подготовить. Экзаменатор задает три вопроса. Найти вероятности событий: Ответ:1) Р(А)=8/11; 2)Р(В)=2/33; 3)Р(С)=2/11 Пять студентов случайным образом оказались в очереди в библиотеку. Ответ: 1) Р(А)=0,4; 2) Р(В)=0,05 Случайным образом набирают шестизначный телефонный номер. Ответ:1) Р(А)=0,1512; 2) Р(В)=(0,4) 6 =0,004096; 3) Р(С)=9 4 /10 6 =0,006561 В лотерее 10 билетов:1 билет — выигрыш 1000 рублей;2билета-по 500 рублей,3 билета -по 100 рублей, а 4 билета — без выигрыша. Студент купил три билета. Ответ: 1) Р(А)=1/12,2) Р(В)=0.1; 3) Р(С)=29/30 Шесть студентов (3 юноши и 3 девушки) случайным образом садятся за круглый стол. Найти вероятности событий: Ответ:1) Р(А)= Для подготовки к контрольной работе преподаватель выдал 12 задач. Студент смог решить только шесть. Контрольная состоит из шести выданных для подготовки задач. Если решены все шесть задач, то оценка «отлично»; если пять, то оценка «хорошо»; если четыре, то оценка «удовлетворительно»; а в остальных случаях студент получит «незачет». 1) На полке 5 красных, 4 белых и 3 синих шара, которые случайным образом переставляют. Найти вероятности событий: Ответ: 1) Р (А)= Ответы: 1) P(A)= Для получения повышенной стипендии на факультете менеджмента отобрали 10 кандидатов: три студента 1го курса, 4 студента второго курса, 2 студента третьего курса и одного студента 4 курса. Фонд стипендий рассчитан только на пять студентов. Случайным образом отобрали пять студентов для получения стипендии. Ответ: 1) P(A)= На книжной полке стояли книги одного автора, при этом : I том – 4 экземпляра, II том – 2 экземпляра, III том – 5 экземпляров, IV том – 1 экземпляр. Книги случайным образом переставили Ответ: 1) P(A)= В новогодней лотерее 12 билетов: один билет – 10000 рублей, два билета по 5000 рублей, 3 билета по 1000 рублей, четыре билета по 100 рублей, а два без выигрыша. Студенту предложили наудачу выбрать четыре билета. Найти вероятности событий: Ответ: 1) P(A) = Брошены две игральные кости. Найти вероятности следующих событий: Ответ: 1) P(A) = Буквы А, А, А, Е, И, К, М, М, Т, Т написаны на определенных карточках. Каждая карточка берется в случайном порядке и прикладывается одна к другой. Ответ: P(B)= Десять студентов, среди которых Иванов и Петров, размещаются в гостинице в два трехместных и один четырехместный номер. Сколько существует способов их размещения? Ответ: n(Ω)= P(A)= После первой волны зачисления в ВУЗ по результатам ЕГЭ оказалось, что в группе №1 есть три вакантных места, в группе №2 есть четыре вакантных места, а в группе №3 есть два вакантных места. 1) Сколько способов распределить новых 9 абитуриентов по трем группам? Ответ: 1) n(Ω)= 2) n(A)= P(A)= В цветочный магазин привезли свежие цветы: 1) розы; 2)тюльпаны; 3)гвоздики; 4) хризантемы; 5)лилии; 6)ирисы. 1)Сколько всевозможных букетов можно составить из семи цветов? Ответ: 1. n(Ω)= 2. n(A)= Преподаватель случайным образом раздал 12 перенумерованных задач четырем студентам 1.Сколько способов раздать задачи? так, что каждый получил по три задачи. 2. Найти вероятность события: Ответ: 1. n(Ω)= 2. n(A)= P(A) Найти вероятность того, что из 52 карт последовательно будут вытащены: «тройка», «семерка», «туз». Ответ: P(A)= Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке. Источник |

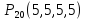 =
=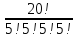 (смотр формулу (*))
(смотр формулу (*))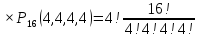 =
=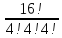
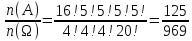
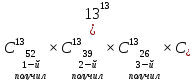 =1
=1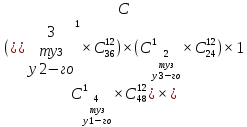
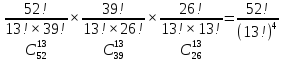
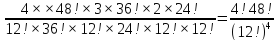
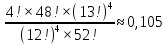
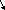


 =
=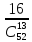 =
=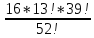 ≈8,4*10 -12
≈8,4*10 -12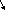
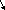

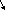
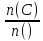 =
=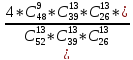 =
=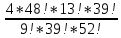 ≈0,01056
≈0,01056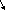
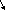
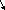
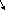
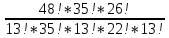 =
=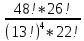
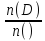 =
=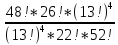 ≈0,0552
≈0,0552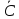 10 6 = C 10 (10+6-1) =C 10 15
10 6 = C 10 (10+6-1) =C 10 15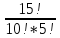 =3003
=3003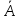 =
=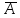 )=
)= 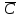 10 5 = C 10 14 =
10 5 = C 10 14 = 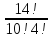 = 1001
= 1001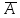 )=-
)=-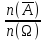 -=
-= 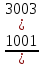 = 1/3
= 1/3 =1/30; 2)Р(В)=
=1/30; 2)Р(В)=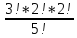
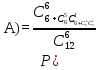 =
= 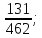 2)P(B)=
2)P(B)=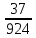 ; 3)P(C)= 1-P(A)=
; 3)P(C)= 1-P(A)= 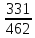
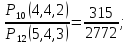 2) Р(В)=
2) Р(В)=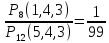 .
.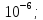 2) P(B)=
2) P(B)= 3)P(C)=
3)P(C)=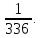
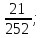 2) P(B)=
2) P(B)=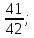 3) P(C)=
3) P(C)=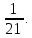
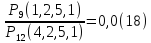 ; 2) P(B)=
; 2) P(B)=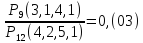 .
.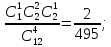 2) P(B) =
2) P(B) =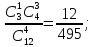 3) P(C)=1.
3) P(C)=1.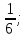 2) P(B)=
2) P(B)=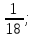 3) P(C)=
3) P(C)= .
.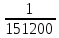
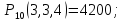
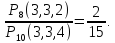
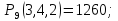
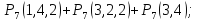
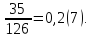
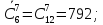
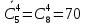 P(A)=
P(A)=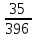
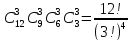 ;
;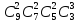
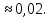
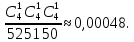 n(Ω)=
n(Ω)=