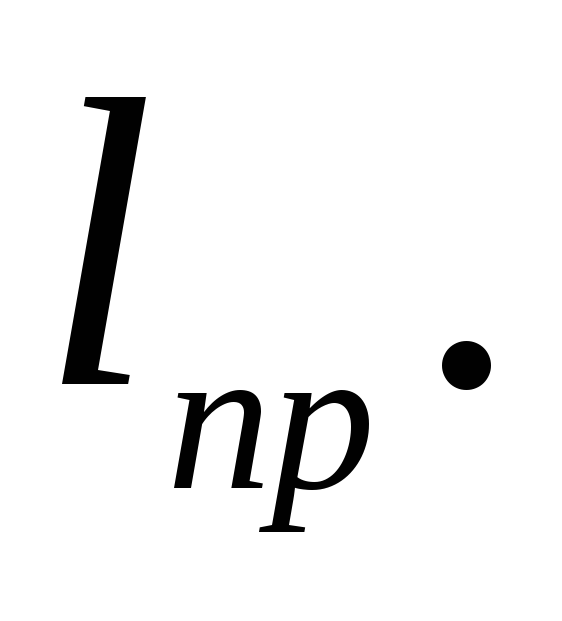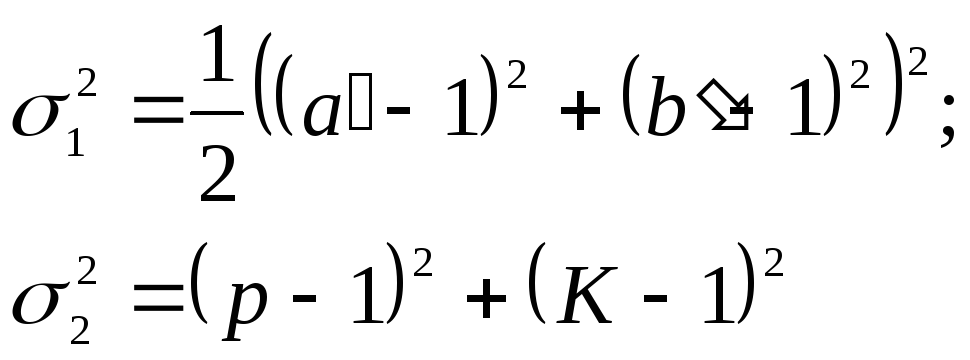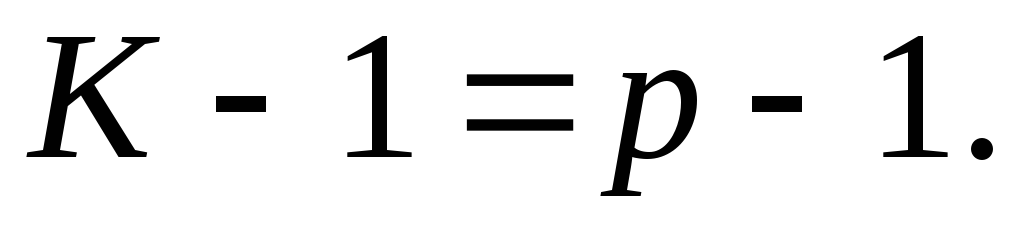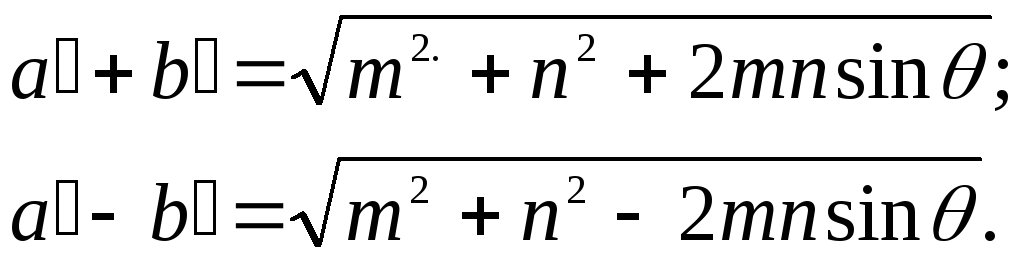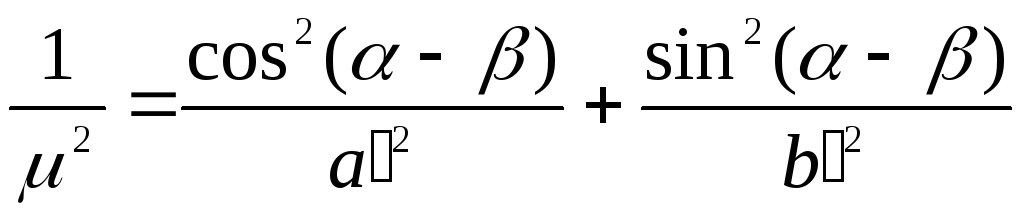Основные определения. Определение 2.5. Картографической проекцией называют математически определенный способ отображения поверхности геоида (эллипсоида) на плоскости
Определение 2.5. Картографической проекцией называют математически определенный способ отображения поверхности геоида (эллипсоида) на плоскости. Картографическая проекция устанавливает соответствие между географическими (геодезическими) координатами точек геоида (земного эллипсоида, шара ) и прямоугольными координатами тех же точек на плоскости.
Эта зависимость в географической системе координат может быть выражена в общем виде двумя уравнениями
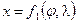
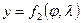
называемыми уравнениями картографических проекций.
В геодезической системе координат также используется два уравнения
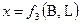
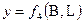
Каждая пара уравнений позволяет вычислять прямоугольные координаты x и y изображаемой точки по геодезическим координатам B и L или по координатам j и l в случае географической системы координат. Число возможных функциональных зависимостей не ограничено. Необходимо только, чтобы изображение было однозначным и непрерывным (рис. 2.8).
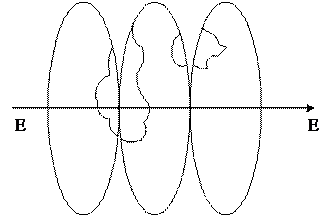 | 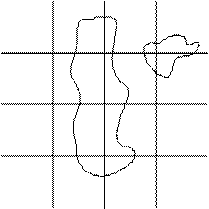 |
| а | б |
| Рис. 2.8. Формирование непрерывного изображения а – объекты на поверхности эллипсоида, б – изображение объектов на карте |
Поскольку поверхность геоида, эллипсоида или шара даже нельзя развернуть в плоскости без искажений, непрерывность и однозначность изображения на плоскости достигаются как бы за счет неравномерной деформации поверхности геоида, эллипсоида или шара при совмещении её с плоскостью. Отсюда следует, что масштаб изображения объектов на плоскости не может быть постоянным. Причем меняется масштаб не только от точки к точке, но и в одной и той же точке в зависимости от направления.
Определение 2.6. Главный масштаб длин – это масштаб, который показывает во сколько раз уменьшены линейные размеры объектов на поверхности эллипсоида[2] или шара при их отображении на карте. Он сохраняется не по всей карте, а только в отдельных ее точках или линиях, где нет искажения длин.
Линейный масштаб во всех остальных точках характеризуется частным масштабом длин, выраженным в долях главного масштаба.
Определение 2.7. Частным масштабом длин называют отношение длины бесконечно малого отрезка на карте dS’ к длине соответствующего бесконечно малого отрезка dS на поверхности эллипсоида или шара
На карте чаще всего подписывается главный масштаб длин.
Определение 2.8. Главный масштаб площадей есть отношение, показывающее во сколько раз уменьшены площадные размеры поверхности эллипсоида или шара при их отображении на карте.
Он сохраняется на картах только в тех местах, где нет искажений площадей. В других местах карты масштабы площадей отличаются от главного и их называют частными масштабами площадей.
Источник
2.3. Понятие о картографических проекциях
Картографическая проекция – математически определенное отображение поверхности земного эллипсоида на плоскости. При этом на карте передаются положения и очертания картографируемых объектов, а также сетка меридианов и параллелей. Закон, определяющий картографическую проекцию, может быть выражен:
1. Ее уравнениями;
2. Указанием графического построения;
3. Таблицей координат и другими способами.
Уравнением картографической проекции называют два уравнения, определяющие связь между координатами точек на карте и соответствующих точек на поверхности эллипсоида.
Координатные сетки – это картографическая, прямоугольная, километровая и другие сетки. Картографическая сетка – есть изображение параллелей и меридианов на карте.
Прямоугольная сетка на карте – это координатная сетка в системе плоских прямоугольных координат в данной картографической проекции.
Километровая сетка – это координатная сетка, линии которой проведены на карте через интервалы, соответствующие определенному числу километров. Точки пересечения линий координатной сетки на карте называют узловыми точками.
2.4. Искажения в картографических проекциях
Карте присущи искажения длин, площадей, углов и форм.
1. Искажения длин выражаются в том, что масштаб длин на карте изменяется при переходе от одной точки к другой, а также при изменении направления в данной точке;
2. Искажения площадей возникают из-за того, что масштаб площадей в разных местах карты различен;
3. Искажения углов заключаются в том, что углы между направлениями на карте не равны соответствующим углам на земной поверхности. Углы между линиями географических объектов искажены, что приводит к нарушению форм самих объектов;
4. Искажения форм заключаются в том, что фигуры объектов на карте не подобны соответствующим географическим фигурам на местности.
Все виды искажений на карте связаны друг с другом, и изменение одного из них влечет за собой изменения других. Особый характер имеет связь между искажениями площадей и углов. Уменьшение одного из них влечет увеличение другого. Нет карт без искажений, однако имеются карты, в которых либо отсутствуют искажения углов, либо отсутствуют искажения площадей, либо искажения углов и площадей как бы уравновешены.
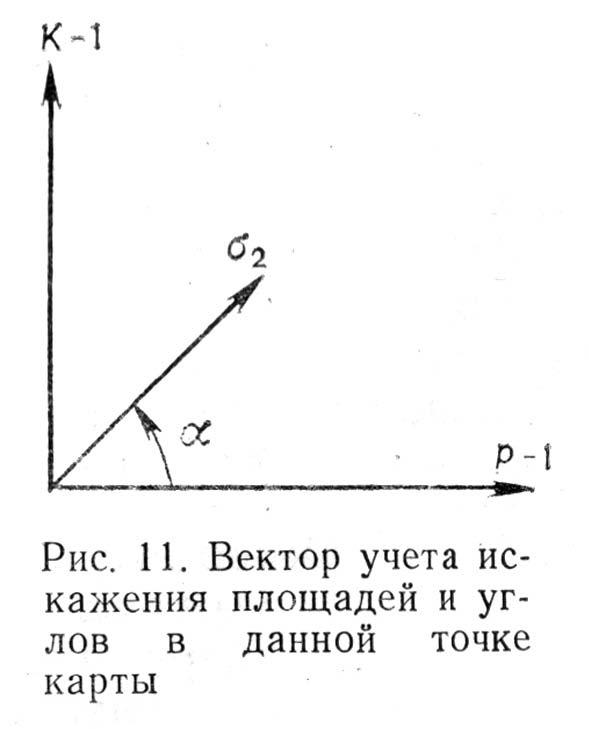
Показателем искажений длин в данной точке по данному направлению является частный масштаб длин µ, выражаемый в долях главного масштаба. Он может быть больше главного (например, 2,32) и меньше его (например, 0,81). Масштаб µ меняет свою величину в данной точке в зависимости от направления. По одному из направлений в данной точке масштаб длин имеет наибольшее, а по другому – наименьшее значение. Эти направления взаимно перпендикулярны, и их называют главными направлениями. Наибольший масштаб длин обозначим через 
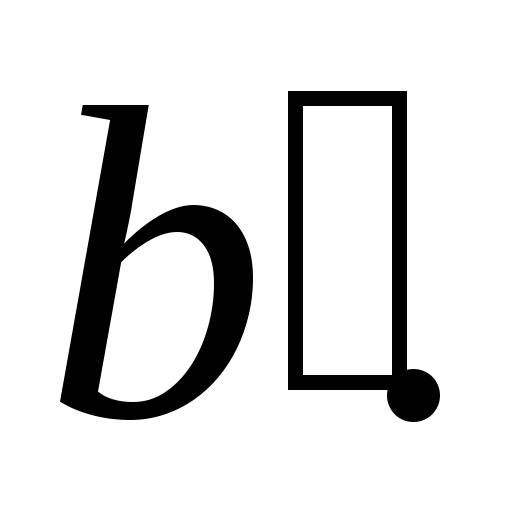






Показатели искажений площадей принимают частный масштаб площадей 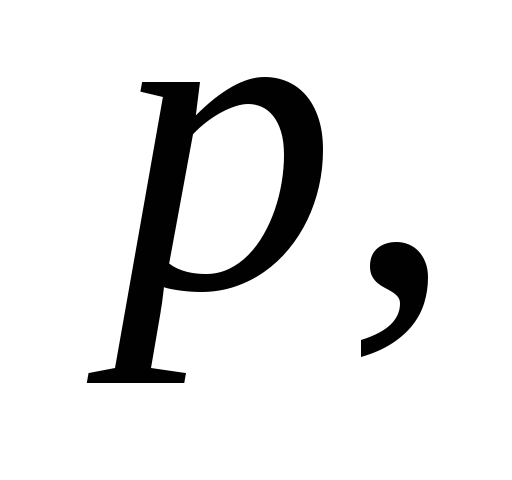

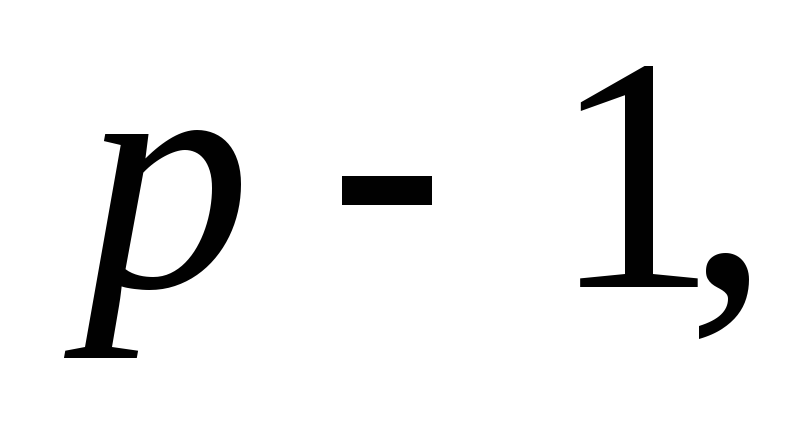
Рис. 2.1. Элементарный сфероидический треугольник
Величина искажения угла в данной точке карты зависит от направления сторон угла. Поэтому в качестве показателя искажения углов на карте принято наибольшее искажение 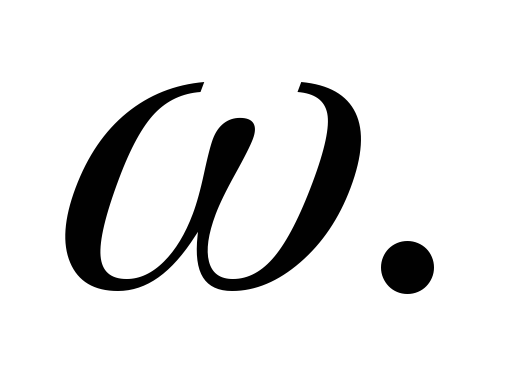



Искажения форм (как и углов) являются следствием того, что частный масштаб длин по разным направлениям различен. Поэтому отношение 
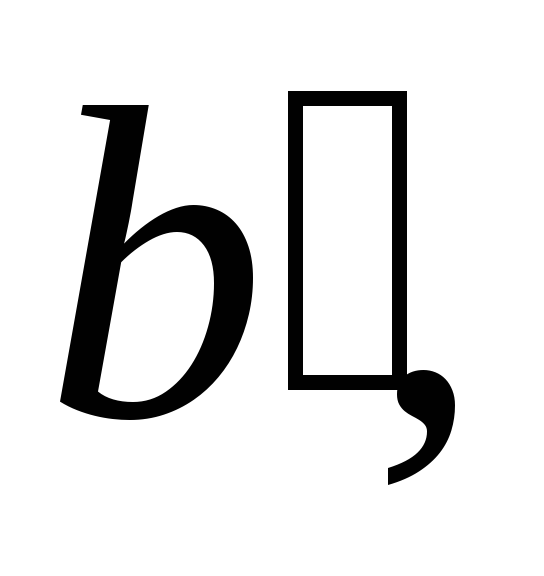

Показатель 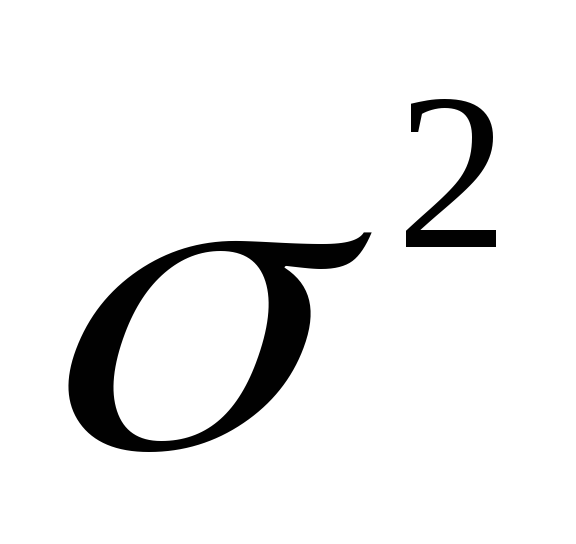

Он характеризует соотношения площадей и искажений углов.
При 
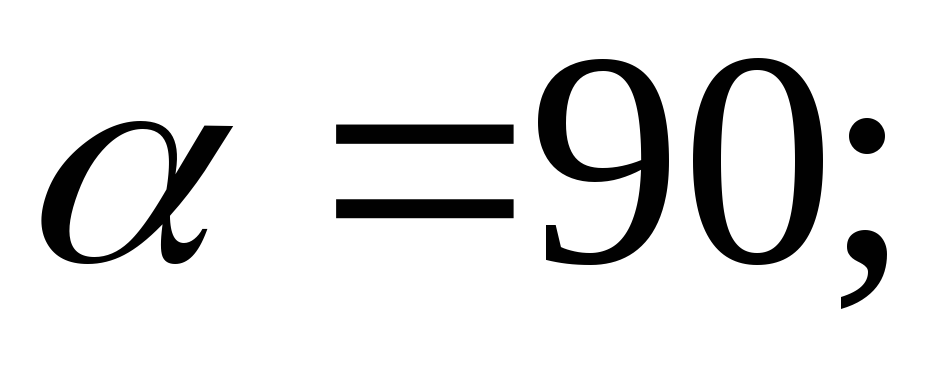

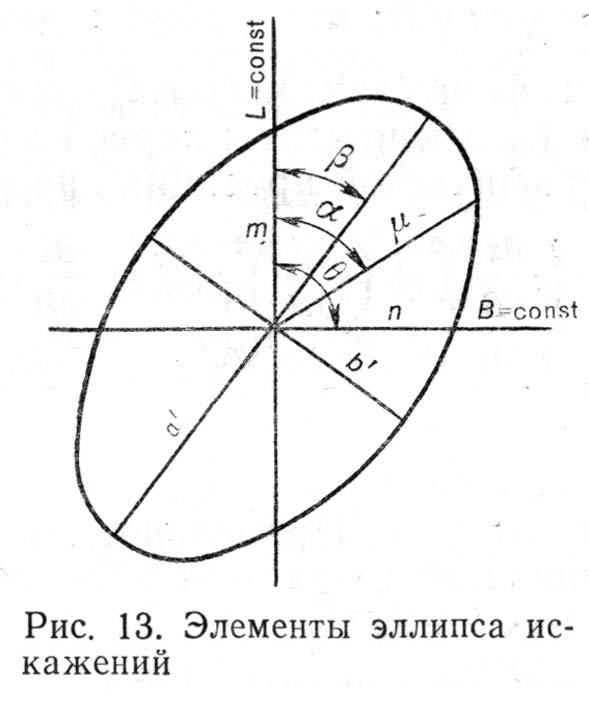
Наиболее точно все виды искажений в данной точке карты можно представить в виде эллипса искажений (рисунки 12 и 13). Эллипс искажений в данной точке карты изображает бесконечно малый круг на поверхности относимости. Его полуоси равны величинам 
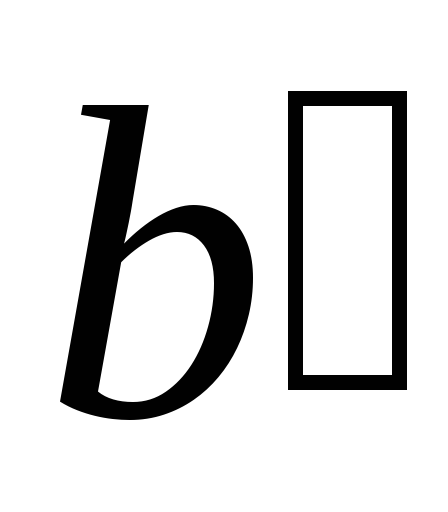
Их можно сравнивать и сопоставлять с показанными на карте, где нет искажений или отсутствует один из видов искажений. Величина и характер искажений, который каждый эллипс демонстрирует, следует относить к точке карты, в которой находится центр эллипс.
Определяя на карте или вычисляя по формулам частные масштабы длин по меридианам 
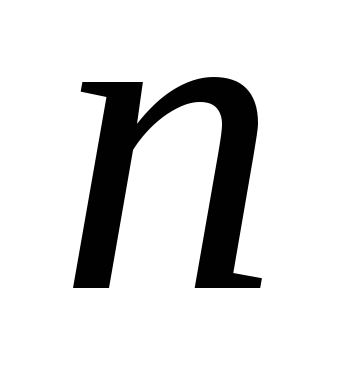



Азимут на карте большой оси эллипса вычисляют по формуле:
Зная 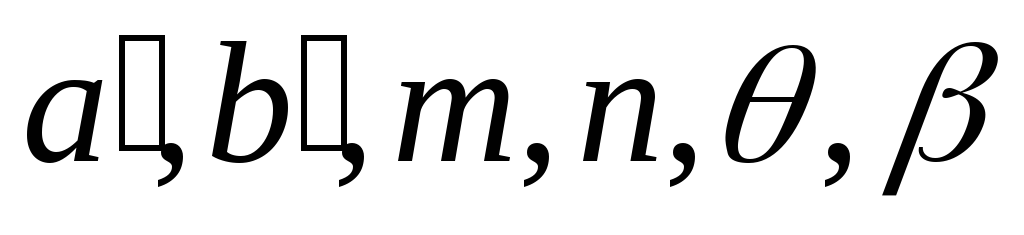


В пределах карты величины искажений изменяются. В некоторых картографических проекциях имеются центральные точки или линии, в которых искажений (обычно углов) невелики и с удалением от них вначале медленно, а затем ускоренно возрастают. Скорость этого возрастания в разных направлениях может быть различной. Обычно на картах имеются точки или линии, в которых искажения отдельных или всех видов отсутствуют. Это точки и линии нулевых искажений. Места на карте с максимальными искажениями обычно наиболее удалены от линий или точек нулевых искажений. Чтобы обеспечить возможно меньшую величину максимальных искажений, точку или линию нулевых искажений располагают в центре карты. Когда линия замкнута или имеются две линии, их располагают так, чтобы удаления от них к середине и краям карты были примерно одинаковыми. Как изменяются искажения при удалении от точек или линий центральных или нулевых искажений, удобно показывать изоколами.
Изоколы – линии, соединяющие точки с одинаковой величиной того или иного показателя искажений. Изоколы показывают на макетах карты. Обычно в некоторых атласах, а также в учебных пособиях по математической картографии приводятся макеты с изоколами 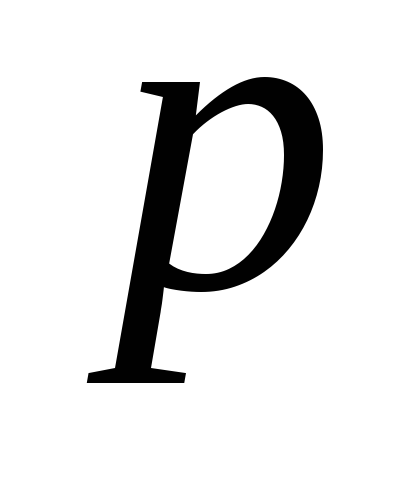
Другой способ показа величин искажений – это составление таблиц с определенным набором показателей искажений.
Выше были рассмотрены локальные показатели. Они характеризуют искажения в точке карты. Иногда при выборе, при искажениях с целью сопоставления разных вариантов проекций пользуются показателями искажений, характеризующими карту в целом. Применяют показатель вариационного типа:
где 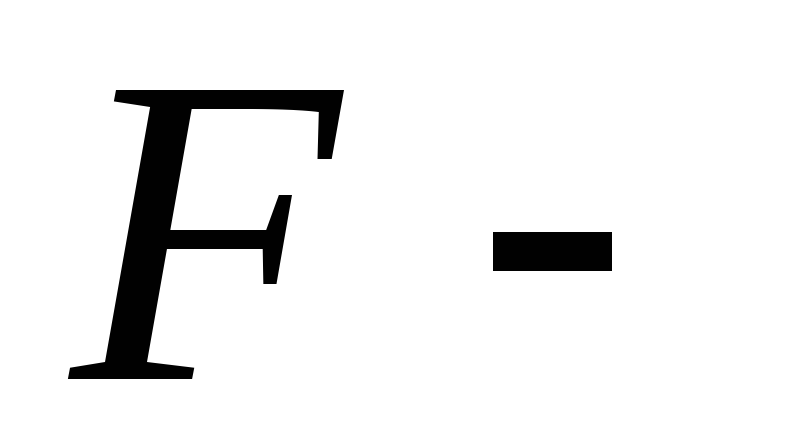
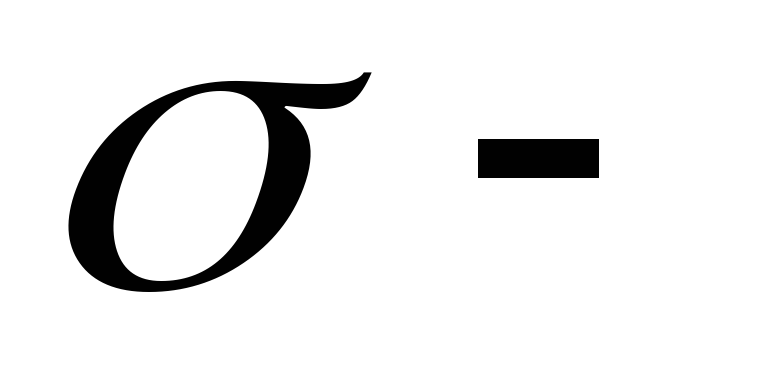


Источник