Каркасный способ задания поверхности
Поверхность рассматривается как геометрическое место точек, координаты которых удовлетворяют некоторому заданному уравнению вида F(x,y,z)=0 (рис. 48, а, б, в). Порядок уравнения соответствует порядку поверхности. Порядок поверхности можно определить и геометрически, как порядок кривой, по которой плоскость пересекает поверхность, или как число точек пересечения прямой с поверхностью.


б – гиперболоид однополостный
в – гиперболический цилиндр
Аналитический способ задания поверхности находит широкое применение в практике, особенно если требуется исследовать свойства поверхности.
Кинематическую поверхность можно рассматривать как непрерывную совокупность последовательных положений линии, перемещающейся в пространстве по некоторым неподвижным линиям. Таким образом, на любой кинематической поверхности можно выделить два семейства линий: семейство образующих и семейство направляющих. Направляющие и образующие обладают следующим свойством: никакие две линии одного семейства не пересекаются между собой, но каждая линия одного семейства пересекает все линии другого.
Рассмотрим формирование конической поверхности (рис. 49). Такая поверхность образована движением прямой образующей l, постоянно проходящей через точку S и во всех своих положениях пересекающей некоторую направляющую кривую m. Если направляющая m – окружность, каждая точка которой равноудалена от вершины S, образуется прямой круговой конус.
Совокупность точек, линий и различных условий, определяющих закон перемещения образующей, называют также определителем поверхности. Например, определителем конуса вращения могут быть ось и образующая или вершина и направляющая линия. Определителем цилиндра вращения может быть ось и образующая (прямая или кривая) или ось и направляющая (окружность). Окружность может быть и направляющей линией цилиндра и его образующей. В начертательной геометрии все поверхности рассматриваются как кинематические, то есть образованные непрерывным перемещением в пространстве какой – либо линии или поверхности.

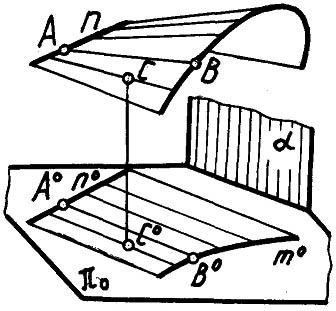
Поверхности, к которым нельзя применить математические закономерности или поверхности с произвольными образующими называются скульптурными или поверхностями произвольных форм (рис. 50). Такие поверхности обычно задают достаточно плотной сетью линий и точек, принадлежащих этим поверхностям. Совокупность таких линий называется каркасом поверхности. При этом точки, лежащие между линиями каркаса, определяются приближенно.
Одним из наиболее распространенных в промышленности методов конструирования поверхностей является метод конструирования с помощью непрерывного каркаса. Метод каркасного конструирования используется при изготовлении кузовов автомобилей, самолетов и в судостроении, для выполнения штампов при изготовлении поверхностей из листового материала, в топографии, горном и дорожном деле.
Источник
Глава IX. Поверхности §24. Определитель поверхности. Каркасный и кинематический способы задания поверхности
Поверхность представляет собой закономерное или незакономерное непрерывное множество точек.
Закономерные поверхности могут быть описаны алгебраическими или трансцендентными уравнениями. Задание поверхности уравнением — аналитический способ задания.
Если поверхность описывается алгебраическим уравнением n-ой степени, то поверхность считается n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка, какой имеет поверхность (рис.1.150).
Порядок поверхности может быть определен числом точек ее пересечения с произвольной прямой (см. рис.1.150).
В начертательной геометрии поверхность рассматривают как множество всех последовательных положений движущейся линии. Эта линия называется образующей. Закон движения образующей в пространстве определяется неподвижными линиями — направляющими. Такой способ образования и задания поверхностей называется кинематическим (рис.1.151).
При этом способе образования поверхность считается заданной, если можно определить положение и форму образующей в любой момент ее движения, а это позволит ответить на вопрос, принадлежит ли точка пространства поверхности или нет (рис.1.151). Для однозначного определения поверхности заданы геометрические элементы (Г), определяющие образующую и направляющие, и алгоритм [A] формирования поверхности из этих геометрических элементов. Совокупность этих двух условий называют определителем поверхности σ(Г)[A]. Например, определитель цилиндрической поверхности σ(s, m)[А] (рис.1.152); геометрическая часть (s, m) — направление образующей и направляющая; алгоритмическая [A] — образующая движется, оставаясь все время параллельной заданному направлению s.
Чтобы задать поверхность на чертеже, нет необходимости указывать проекции всего множества линий, принадлежащих поверхности, достаточно указать проекции элементов, входящих в состав определителя. Например, на рис.1.152 задана цилиндрическая поверхность.
В зависимости от формы образующей, поверхности могут быть линейчатые, образующей которых является прямая линия, и нелинейчатые, образующая которых криволинейная. Нелинейчатые поверхности могут быть с образующей постоянного вида — поверхности, образующие которых не изменяют своей формы в процессе образования поверхности, и с образующей переменного вида — такие, образующая которых изменяется в процессе образования поверхности.
§25. Классификация поверхностей. Поверхности линейчатые
Различают линейчатые поверхности с одной направляющей, с двумя направляющими, с тремя направляющими.
Линейчатые поверхности с одной направляющей (торсы) образуются движением прямой линии, перемещающейся по определенному закону по одной направляющей.
К этой группе поверхностей относятся:
— поверхности с ребром возврата.
Цилиндрическая поверхность (рис.1.153) образуется движением прямой линии по кривой направляющей m.
Образующая во всех положениях (l1…l6) параллельна заданному направлению s. Определитель поверхности σ(s, m)[A]. При пересечении поверхности плоскостью π0 получается след поверхности n.
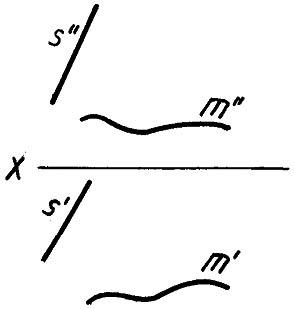
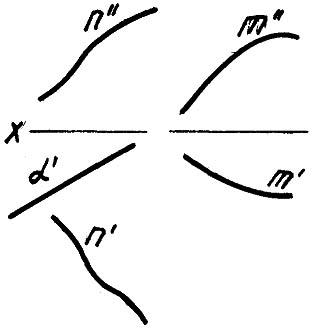
Поверхность на чертеже может быть задана проекциями направляющей m (m’, m») и проекциями направления s (s’, s») (рис.1.154).
На чертеже также построен горизонтальный след n (n’, n») поверхности, который зачастую используется в качестве направляющей при задании чертежа поверхности.
Точки, принадлежащие цилиндрической поверхности, могут быть построены на ее чертеже при помощи проходящих через них образующих. Зачастую следует указывать, считается точка видимой или невидимой.
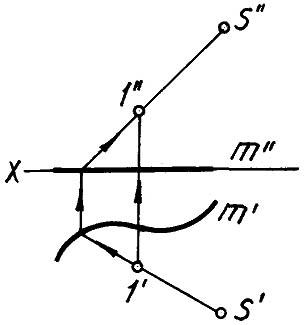
На рис.1.155 стрелками показано построение горизонтальной проекции точки 1, принадлежащей поверхности с заданной проекцией 1″.
Указано, что на плоскости π1, точка 1 невидимая.
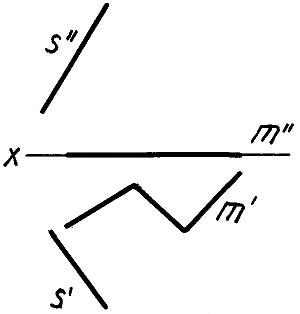
Если направляющая — ломаная линия, то получим призматическую поверхность (рис.1.156).
Если в нормальном сечении цилиндрической поверхности плоскостью (плоскость перпендикулярная образующим) получается неопределенная кривая, то имеем цилиндрическую поверхность общего вида.
Когда нормальное сечение — кривая второго порядка, то имеем цилиндрическую поверхность второго порядка. Различают цилиндр второго порядка эллиптический (круговой), параболический, гиперболический.
Коническая поверхность (рис.1.157) образуется движением прямой линии по кривой направляющей m, при этом образующие проходят через неподвижную точку S.
Определитель поверхности σ(m, s)[А]. На чертеже коническая поверхность задается проекциями направляющей m и точки S — вершины конуса. В качестве направляющей зачастую используют след поверхности на плоскости проекций (рис.1.157).
На рис.1.158 показано построение проекций точки 1, принадлежащей конической поверхности.
Частным случаем конической поверхности является поверхность пирамидальная. В этом случае направляющая поверхности — ломаная линия.
Коническая поверхность будет поверхностью второго порядка, когда направляющей поверхности является кривая второго порядка.
Поверхность с ребром возврата образуется непрерывным движением прямой линии (образующей), во всех своих положениях касающейся некоторой пространственной кривой (направляющей). Такая поверхность показана на рис.1.159.
Пространственная кривая — направляющая, называется ребром возврата, она делит поверхность на две полости.
Кривые линейчатые поверхности с одной направляющей являются поверхностями развертываемыми, то есть они могут быть всеми своими точками совмещены с плоскостью, не претерпевая каких-либо повреждений (разрывов, складок).
Все кривые нелинейчатые поверхности и те линейчатые, которые не могут быть развернуты в плоскость, называются неразвертываемыми.
Линейчатые поверхности с двумя направляющими (криволинейными или прямолинейными).
Образующая при этом сохраняет постоянный угол с некоторой плоскостью.
Ограничимся рассмотрением случаев, когда образующая параллельна плоскости (поверхности с плоскостью параллелизма).
Определитель этой группы поверхностей σ(m, n, α)[A], где m, n — направляющие; α — плоскость параллелизма.
К числу поверхностей с плоскостью параллелизма относятся:
— цилиндроид (рис.1.160), когда обе направляющие являются кривыми линиями;
— коноид (рис.1.161) когда одна из направляющих — прямая линия;
— косая плоскость (рис.1.162), когда обе направляющие — прямые линии.
Чтобы задать эти поверхности на чертеже, достаточно указать проекции направляющих и плоскости параллелизма (рис.1.163).
Задачи, связанные с построением проекций точек, принадлежащих поверхности с плоскостью параллелизма, рассмотрены в §27.
Винтовая поверхность образуется при движении прямой линии по двум направляющим, одна из которых винтовая линия, другая — ось винтовой линии. Из определения следует, что винтовая поверхность является коноидом. Ось винтовой линии пересекается с образующей под постоянным углом. Если этот угол равен 90°, то образуется прямая винтовая поверхность. Если угол не равен 90°, то винтовая поверхность носит название косой.
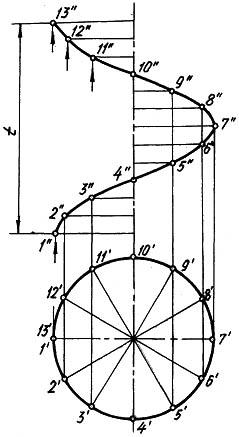
Прямая винтовая поверхность изображена на рис.1.164.
В сечении такой поверхности плоскостью, проходящей через ось или перпендикулярной оси, получается образующая поверхности.
В случае косой винтовой поверхности (рис.1.165) образующая сохраняет постоянный не равный 90° угол наклона к оси поверхности.
Следовательно, в этом случае проекции образующих на ось — величина постоянная (отрезок l на рис.1.165). Это используют при построении фронтальной образующей в любом положении. Расстояние t (рис.1.164, рис.1.165), на которое перемещается образующая винтовой поверхности, и совершает полный поворот вокруг оси винтовой линии — шаг винтовой поверхности.
Задачи, связанные с построением на чертеже проекций точки, принадлежащей винтовой поверхности, рассмотрены в §27.
Если плоская фигура (квадрат, треугольник, трапеция) движется по поверхности цилиндра так, что ее вершины перемещаются по винтовым линиям, а плоскость самой фигуры постоянно проходит через ось цилиндра, то получается винтовой выступ, ограниченный винтовыми и цилиндрическими поверхностями (рис.1.166, рис.1.167).
Построение проекций выступа сводится к построению винтовых линий — траекторий вершин движущейся плоской фигуры. Совокупность цилиндра и винтового выступа на нем называют винтом.
Винты с резьбой различного профиля (треугольной, квадратной, трапецеидальной и др.) широко применяются в технике в элементах соединения деталей, ходовых, грузоподъемных, транспортирующих и др. устройствах (см. рис.1.168, рис.1.169).
Линейчатые поверхности с тремя направляющими (рис.1.170) образуются движением прямой линии по трем направляющим (криволинейным или прямолинейным).
Положение образующих в этом случае однозначно определяется формой и положением в пространстве направляющих m, n, k. Определитель поверхности этой группы имеет вид σ(m, n, k).
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник