Калькулятор матриц способ треугольника

Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.

Используя этот онлайн калькулятор для вычисления определителя (детерминанта) матриц, вы сможете очень просто и быстро найти определитель (детерминант) матрицы.

Воспользовавшись онлайн калькулятором для вычисления определителя (детерминанта) матриц, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на транспонирование матриц, а также закрепить пройденный материал.

Найти определитель (детерминант) матрицы

Введите значения Матрицы:

Ввод данных в калькулятор для вычисления определителя (детерминанта) матриц

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления определителя (детерминанта) матриц

• Между полями для ввода можно перемещаться нажимая клавиши , , и на клавиатуре.

Теория. Определитель (детерминант) матрицы.

Вычисление определителя матрицы 2×2

Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:

∆ =

a 11 a 12 a 21 a 22

= a 11· a 22 — a 12· a 21

Правило треугольника для вычисления определителя матрицы 3×3

Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

+	–

∆ =

a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33

=

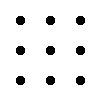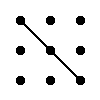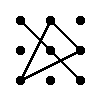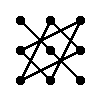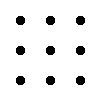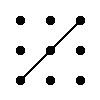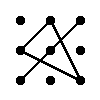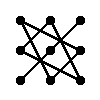Вычисление определителя матрицы произвольного размера

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Источник

Решение задач с матрицами.

Матричный калькулятор

Очистить	Размер ×
Транспонировать	Умножить на
Найти определитель	Возвести в степень
Найти ранг	Найти обратную

Очистить	Размер ×
Транспонировать	Умножить на
Найти определитель	Возвести в степень
Найти ранг	Найти обратную

Ввод данных в матричный калькулятор

В матричный калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности матричного калькулятора

• Между полями для ввода можно перемещаться нажимая клавиши , , и на клавиатуре.

Теория. Матрицы

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Калькулятор матриц — действия с матрицами онлайн

С помощью калькулятора матриц вы сможете выполнять различные преобразования матриц, решать СЛАУ, а также находить некоторые характеристики, как, например, определитель, след и ранг. Подробнее о функционале и использовании калькулятора смотрите после блока с самим калькулятором.

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: a T _ij = a_ji

Как пользоваться калькулятором матриц

1. Выберите матрицу (или матрицы) с помощью переключателей ( )
2. Укажите размер с помощью выпадающих списков под матрицей ( × )
3. Заполните элементы (нулевые элементы можно не заполнять.)
4. Выберите в выпадающем списке требуемую функцию и, если требуется, введите дополнительные параметры.
5. Нажмите кнопку .
6. Если вывод чисел не устраивает, просто поменяйте его — доступны три варианта представления: правильные дроби (2

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби ( 1/2 , 29/7 , -1/125 ), десятичные дроби ( 12 , -0.01 , 3.14 ), а также числа в экспоненциальной форме ( 2.5e3 , 1e-2 ).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки ( ← , ↑ , → , ↓ ) для перемещения по элементам

Что умеет наш калькулятор матриц?

Вычисление выражений с матрицами

Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.

Из чего могут состоять выражения?

• Целые и дробные числа
• Матрицы A, B
• Знаки арифметических действий: + — * /
• Круглые скобки для изменения приоритета операций: ( )
• Транспонирование: ^T
• Возведение в целую степень: ^

Примеры корректных выражений

• Cложение двух матриц: A+B , (A)+(B) , ((A) + B)
• Возведение линейной комбинации матриц в степень: (3A — 0.5B)^5
• Произведение транспонированной матрицы на исходную: A^TA
• Обратная матрица в квадрате для B: B^-2

Что такое матрица?

Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами. Матрицы обозначаются заглавными латинскими буквами. При необходимости размер записывается следующим образом: A_n×m .

Примеры матриц

1	0	0	0
0	1	0	0
0	0	1	0
0	0	0	1

2	-1	0	0
-3	2	0	0
31	-19	3	-4
-23	14	-2	3

Элементы матрицы

Элементы A обозначаются a_ij , где i — номер строки, в которой находится элемент, j — номер столбца.

Некоторые теоретические сведения

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: a T _ij = a_ji

Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали — a_ii

Единичная матрица E_n×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.

Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение: rank(A)

След — это сумма элементов, находящихся на её главной диагонали. Обозначение: tr(A) или track(A)

Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.

Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение: A n

Обратная матрица A −1 — матрица, произведение которой на исходную матрицу A равно единичной матрице: A -1 ×A = A×A -1 = E

Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.

LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. A = L·U

Сложение матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: с_ij=a_ij+b_ij

Разность матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: с_ij=a_ij-b_ij

Умножение матриц A_n×k и B_k×m — матрица C_n×m, у которой элемент (c_ij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B: c_ij = a_i1·b_1j + a_i2·b_2j + . + a_ik·b_kj

Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.

Источник

Определитель матрицы онлайн

Вычислить определитель матрицы онлайн можно различными способами с помощью нашего сервиса. Решение бесплатное с пошаговыми действиями и пояснениями.

Определитель матрицы – это сумма слагаемых всевозможных произведений элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы, при этом знак произведения определяется четностью перестановки.

Описание калькулятора определителя матрицы

Данный калькулятор поможет научиться находить определитель матрицы различными способами:

• используя метод Гаусса
• с помощью Правила треугольников
• по Правилу Саррюса
• с использованием формулы Лейбница
• методом Гаусса-Монтанте (алгоритм Барейса)

Наш сервис не только позволяет получить определитель матицы, но и предоставляет последовательность решения с комментариями и пояснениями в режиме онлайн, бесплатно. Так же калькулятор может быть полезен при проверке правильности выполненного самостоятельно решения.

Заполните поля для элементов матрицы и нажмите соответствующую кнопку.

• С помощью плюса и минуса выберите нужный размер матрицы. Если нужна неквадратная матрица, то просто ненужные ячейки оставьте пустыми.
• Внесите значение элементов матрицы в ячейки. Значения могут быть:
  • целые числа: 7 , -3 , 0
  • десятичные (конечные и периодические) дроби: 7/8 , 6.13 , -1.3(56) , 1.2e-4
  • арифметические выражения: 1/2+3*(6-4) , (6-y)/x^3 , 2^0.5
• Нажмите на кнопку с названием нужной математической операции.
• Значения в результатах решения можно с помощью мышки перетаскивать на различные поля. Например, полученную матрицу можно перетащить на поле исходных данных, для дальнейшего решения.

Источник

Приведение матрицы к треугольному виду

Приведение матрицы к треугольному виду методом Гаусса и методом Барейса.

Ниже два калькулятора для приведения матриц к треугольному, или ступенчатому, виду. Первый использует для этого метод Гаусса, второй — метод Барейса. Описание методов и немного теории — под калькуляторами.

Приведение матрицы к треугольному виду (метод Гаусса)

Приведение матрицы к треугольному виду (метод Барейса)

Итак, для начала определимся с понятием треугольной, или ступенчатой матрицы:
Матрица имеет ступенчатый вид, если:

1. Все нулевые строки матрицы стоят последними
2. Первый ненулевой элемент строки всегда находится строго правее первого ненулевого элемента предыдущей строки
3. Все элементы столбца под первым ненулевым элементом строки равны нулю (это впрочем следует из первых двух пунктов)

Пример ступенчатой матрицы:
1 0 2 5
0 3 0 0
0 0 0 4

Понятие треугольной матрицы более узкое, оно используется только для квадратных матриц (хотя я думаю, что это не строго), и формулируется проще: треугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю. Строго говоря, это даже определение верхнетреугольной матрицы, но мы будем использовать его. Понятно, что такая верхнетреугольная матрица является также и ступенчатой.

Пример треугольной (верхнетреугольной) матрицы:
1 0 2 5
0 3 1 3
0 0 4 2
0 0 0 3
Кстати, определитель треугольной матрицы вычисляется простым перемножением ее диагональных элементов.

Чем же так интересны ступенчатые (и треугольные) матрицы, что к ним надо приводить все остальные? — спросите вы.
У них есть замечательной свойство, а именно, любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.

Что же такое элементарные преобразования? — спросите вы.
Элементарными преобразованиями матрицы называют следующие операции:

1. перестановка любых двух строк (столбцов) матрицы
2. умножение любой строки (столбца) на призвольное, отличное от нуля, число
3. сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.

И что? — спросите вы.
А то, что элементарные преобразования матрицы сохраняют эквивалентность матриц. А если вспомнить, что системы линейных алгебраический уравнений (СЛАУ) записывают как раз в матричной форме, то это означает, что элементарные преобразования матрицы не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Приведя матрицу системы линейных уравнений AX=B к треугольной форме A’X = B’, то есть, с соответствующими преобразованиями столбца B, можно найти решение этой системы так называемым «обратным ходом».

Чтобы было понятно, используем треугольную матрицу выше и перепишем систему уравнений в более привычной форме (столбец B я придумал сам):

Понятно, что сначала мы найдем , потом, подставив его в предыдущее уравнение, найдем и так далее — двигаясь от последнего уравнения к первому. Это и есть обратный ход.

Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют методом Гаусса. Метод Гаусса — классический метод решения систем линейных алгебраических уравнений. Также его еще называют Гауссовым исключением, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Теперь про сам метод.
Собственно, как можно занулить переменную во втором уравнении? Вычтя из него первое, домноженное на коэффициент
Поясним на примере:

Зануляем во втором уравнении:

Во втором уравнении больше не содержится

Обобщенно алгоритм метода Гаусса можно представить следующим образом:

где N — число строк,
— i-тая строка,
— элемент, находящийся в i-той строке, j-том столбце

И все бы ничего, да и метод отличный, но. Дело все в делении на , присутствующем в формуле. Во-первых, если диагональный элемент будет равен нулю, то метод работать не будет. Во-вторых, в процессе вычисления будет накапливаться погрешность, и чем дальше, тем больше. Результат будет отличаться от точного.

Для уменьшения погрешности используют модификации метода Гаусса, которые основаны на том, что погрешность тем меньше, чем больше знаменатель дроби. Эти модификации — метод Гаусса с выбором максимума в столбце и метод Гаусса с выбором максимума по всей матрице. Как следует из названия, перед каждым шагом исключения переменной по столбцу (всей матрице) ищется элемент с максимальным значением и проводится перестановка строк (строк и столбцов), таким образом, чтобы он оказался на месте .

Но есть еще более радикальная модификация метода Гаусса, которая называется методом Барейса (Bareiss).
Как можно избавиться от деления? Например, умножив перед вычитанием строку на . Тогда вычитать надо будет строку , домноженную только на , без всякого деления.
.
Уже хорошо, но возникает проблема с ростом значений элементов матрицы в ходе вычисления.

Барейс предложил делить выражение выше на и показал, что если исходные элементы матрицы — целые числа, то результатом вычисления такого выражения тоже будет целое число. При этом принимается, что для нулевой строки .

Кстати, то, что в случае целочисленных элементов исходной матрицы алгоритм Барейса приводит к треугольной матрице с целочисленными элементами, то есть без накопления погрешности вычислений — довольно важное свойство с точки зрения машинной арифметики.

Алгоритм Барейса можно представить следующим образом:

Алгоритм, аналогично методу Гаусса, также можно улучшить поиском максимума по столбцу(всей матрице) и перестановкой соответствующих строк (строк и столбцов).

Источник