5. Переключательные функции и способы их задания
5.1. Понятие о переключательных функциях
Функция, принимающая значение из множества 0,1,,k1, аргументы которой принимают значения из этого же множества, называется переключательной функцией (ПФ) или функцией k-значной логики [9].
Это может быть тернарное множество T=<0,1,2>, или множество Q=<0,1,2,3>или другое k-элементное множество.
Такая функция может быть задана таблицей из k n строк, где n – количество аргументов. Например, переключательная функция для n=2 (переменные a, b) и k=3 представлена в табл. 7.
Некоторая трехзначная переключательная функция
В табл. 7 число строк равно числу размещений с повторениями из тернарного множества по двум местам. Подобные таблицы называются таблицами истинности или соответствия.
Получим номер ПФ в троичной системе счисления: 222111000. Здесь каждый разряд – соответствует степени числа 3: 3 22 , 3 21 , 3 20 , 3 12 , 3 11 , 3 10 , 3 2 , 3 1 , 3 0 . При этом 22, 21, 20, 12, 11, 10, 2, 1, 0 – троичные числа, соответствующие значениям переменных a, b.
Можно получить номер ПФ в десятичной системе счисления:
Здесь степени числа три – 8, 7, 6, 5, 4, 3, 2, 1, 0.
Если различных двухзначных ПФ

Выделяется ряд различных элементарных функций [9]:
1) 
2)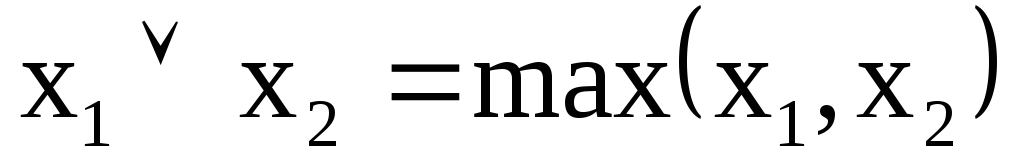
3) 
4) 
5) константы 0,1,2. k-1.
Одноместные функции имеют вид 




Часто таблицы переключательных функций представляют для компактности, как показано в табл. 8-10.
Трехзначная ПФ «дизъюнкция a,b»
Трехзначная ПФ «сумма a,b по модулю 3»
Трехзначная ПФ «a плюс 1 по модулю 3 – циклический сдвиг a»
Функция переключательного типа может быть проиллюстрирована блоком «решение» в схемах алгоритмов [11].
5.2. Двоичные переключательные функции и способы их задания
Функция f, зависящая от n переменных называется двоичной переключательной (булевой), если она и любой из ее аргументов 
Таким множеством может быть бинарное множество 
Произвольная переключательная функция задается одним из способов: матричным (табличным), геометрическим, аналитическим.
При матричном способе переключательная (булева) функция 
Под двоичным набором 

Иногда двоичные наборы в таблицах истинности удобно представлять номерами наборов:
№ набора=
Значения функций на 2 n -наборах также могут быть заданы десятичным номером:
№ функции=
При геометрическом способе ПФ задается с помощью соответствующей отметки вершин n-мерного куба, который, по сути, является решеткой Хассэ, представляющей собой частично упорядоченное множество наборов (каждая вершина – точка n-мерного пространства) [9]. Каждый путь из вершины, соответствующей нулевому набору в вершину единичного набора, соответствует увеличению сравнимых наборов (рис. 28, отношение ).
Рис.28. Геометрическое представление переключательной функции
Этот рисунок изображает частично упорядоченное множество наборов 000, 001, 010, 011, 100, 101, 110, 111, на которых задана переключательная функция трех переменных, например, a, b, c. Вершины, на которых функция равна 1 должны быть как-то отмечены.
Переключательная функция может быть задана и некоторым словесным описанием, указывающим, на каких наборах аргументов какое значение она принимает и исключающим неверное толкование, всякую двусмысленность. Переключательная функция может быть задана перечислением ее рабочих (единичных), запрещенных (нулевых) и условных наборов (на этих наборах функция не определена). Для упорядоченного задания n-мерных наборов переменных функции f(x1,x2. xn) удобно рассматривать их в виде целого неотрицательного числа. При этом младший разряд располагается справа. Например, для переменных х5,х4,х3,х2,х1 конкретное их значение истинности 1,0,0,1,1 соответствует двоичному числу 10011. Это число еще называют номером набора. Для компактной записи наборов значений переменных логической функции, целесообразно представлять их номерами – числами в десятичной, восьмеричной, шестнадцатеричной системах счисления. Такой номер-набор называют еще весовым состоянием или весом этого набора.
В случае использования десятичной системы счисления каждой переменной соответствует степень числа 2 (вес разряда) в зависимости от номера переменной, например, в порядке 2 4 2 3 2 2 2 1 2 0 . Зафиксированный порядок переменных, каждая из которых имеет свой вес, называется базой функции (старший вес – слева). Как мы знаем, переключательная (логическая) функция может быть задана таблицей истинности, которая иногда еще называется таблицей соответствия. Рассмотрим таблицу истинности некоторой недоопределенной логической функции (табл. 11).
Источник
Переключательные функции. Основные базисы. Способы минимизации логических функций
Лекция 7. Переключательные функции. Основные базисы. Способы минимизации логических функций
2. . Способы минимизации логических функций
3.Минимизация булевых функций с помощью карт Карно
1. Набор простейших функций, с помощью которого можно выразить любые другие, сколь угодно сложные логические функции, называется функционально полным набором, или логическим базисом.
Полная система функций называется базисом, если она перестаёт быть полной при исключении из неё любого элемента.
Любую булеву функцию с произвольным количеством аргументов можно построить через подстановку элементарных функций вместо аргументов (суперпозицию).
Существуют базисы состоящие из одной, двух и трех операций, но не более (см. таблицу). Необходимое и достаточное условие для того, чтобы некоторый набор булевых функций обладал достаточной выразительностью, чтобы представить любую булеву функцию, задает Критерий Поста
Число операций, составляющих базис
где ↓ — стрелка Пирса, / — штрих Шеффера, → — имликация
Рассмотрим пример использования базиса <И,НЕ>Пусть есть выражение вида a̅˄b̅ , тогда навесив инверсию над всем выражением и используя закон де Моргана, получим:
2. Способы минимизации логических функций
Аналитические методы минимизации
Используя законы булевой алгебры, можно получить для одной и той же логической функции множество эквивалентных представлений. Чем проще аналитическое выражение функции, тем экономичнее и проще ее практическая реализация на интегральных микросхемах. Сложность булевой функции определяется ее рангом, т.е. количеством переменных в ее конъюнктивных или дизъюнктивных членах.
Представление булевой функции в Сов ДНФ в большинстве случаев не является минимальным.
Используя операции поглощения и склеивания, его можно существенно упростить. Часто используется неполное склеивание, при котором оба члена, участвовавших в склеивании (или один из них), могут повторно склеиваться с другими оставшимися членами Сов ДНФ.
В процессе минимизации важно отыскать смежные конституенты, которые отличаются только одним аргументом (в одну конституенту аргумент входит с инверсией, а в другую – без нее).
Две смежные конституенты, склеиваясь, образуют импликанту рангом на единицу ниже, чем исходные конституенты.
Используя, например, неполное склеивание последней коституенты в Сов ДНФ функции F1 последовательно с остальными, приходим к следующему выражению:
Процесс многоступенчатого склеивания приводит к импликантам, которые не склеиваются с другими. Такие импликанты называют простыми. Форма записи булевой функции в ДНФ, состоящая только из простых импликант, называется сокращенной дизъюнктивной нормальной формой (Сокр ДНФ).
В некоторых случаях в Сокр ДНФ могут содержаться лишние импликанты, которые могут быть исключены без изменения значения функции.
Одним из методов отыскания лишних импликант является метод испытания членов: чтобы испытать некоторый член функции, следует исключить его из Сокр ДНФ и подставить в оставшееся выражение такие значения аргументов, которые обращают исключенный член в единицу. Если при такой подстановке оставшееся выражение окажется тождественно равным единице, то испытуемый член является лишним.
Найдем для примера тупиковую форму Сокр ДНФ

Испытаем член AC. AC = 1, если A = 1 и C = 1. Подставим в оставшееся выражение 

При B = 0 F(A, B, C) = 1·1 Ъ 0·0 = 1, но при 
Испытаем член BC, равный 1 при B = 0, C = 1. При этом

Последнее выражение равно 1 как при A = 1, так и при A = 0. Поэтому член 
Испытание члена 

3.Минимизация булевых функций с помощью карт Карно
Для минимизации функций относительно небольшого числа переменной (не более шести) наиболее простым и наглядным является графический метод, использующий карты Карно.
Карта Карно – это прямоугольник, разбитый на квадраты, число которых равно числу наборов рассматриваемой функции, т. е. 2 n . Клетки размечаются так, чтобы наборы, для которых возможны смежные конституенты, оказались бы в соседних клетках.
При заполнении карты Карно в ее клетки проставляют значения функции для соответствующих наборов, которые являются координатами клеток. Например, для функции двух переменных А и В (рис. 5) карта Карно имеет вид
Единицы, представленные в клетках, обозначают конституенты единицы рассматриваемой функции. Отыскание минимальной ее формы сводится к определению варианта, при котором все конституенты единицы накрываются (охватываются контурами покрытия) наименьшим числом наиболее коротких импликант. Объединение клеток на карте эквивалентно выполнению операции склеивания.
Всегда нужно стремиться к минимальному количеству контуров и максимальной площади каждого из них, руководствуясь следующими правилами:
- площадь контура покрытия должна быть Sk = 2 m-i клеток, где
– целое число, m – число переменных. Если, например, m = 3, то Sk = 1, 2, 4, или 8 клеток;
- число сокращаемых переменных Nперем. = log2 Sk , т.е. при Sk = 1 не сокращается ни одна переменная, при Sk = 2 сокращается одна переменная и т.д.
В примере на рис. 5 пара единиц верхней строки охватывается импликантой Ā (т.е. обе клетки ) имеют общий аргумент Ā). Пара единиц правого столбца накрывается импликантой B, как общей для обеих клеток. Следовательно, минимальная ДНФ функции F(A,B) = Ā Ъ B.
Если имеется несколько вариантов объединения конституент контурами, то можно получить несколько различных эквивалентных минимальных ДНФ функции, одна из которых выбирается для реализации в цифровом устройстве.
Карту Карно удобно использовать и для минимизации функций, заданных в алгебраической форме, например,

Карта Карно, состоящая из 2 3 = 8 клеток, может быть размечена, как показано на рис. 6.
При охвате единиц контурами склеивания карту Карно можно сворачивать в цилиндр, как вдоль горизон-тальной, так и вертикальной оси. В результате все четыре единицы, расположенные в углах Карты, охватываются контуром с общей импликан-той 

· Яблонский С.В. — Введение в дискретную математику
· Конспект лекций О.Б. Лупанова — Введение в математическую логику (2007)
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Источник









 – целое число, m – число переменных. Если, например, m = 3, то Sk = 1, 2, 4, или 8 клеток;
– целое число, m – число переменных. Если, например, m = 3, то Sk = 1, 2, 4, или 8 клеток;



