Каковы способы задания функции спроса

Каковы способы задания функции спроса

Функция спроса (прямая и обратная) с примерами и графиками движения и сдвига

Функция спроса — это математическое уравнение, которое выражает спрос на продукт или услугу в зависимости от его цены и других факторов, таких как цены на заменители и дополнительные товары, доход и так далее.

Функция спроса создает связь между спросом (требуемым количеством) на продукт (который является зависимой переменной) и факторами, влияющими на спрос, такими как цена продукта, цена замещающих и дополняющих товаров, средний доход и прочие (которые являются независимыми переменными).

Давайте рассмотрим рынок приложений для найма автомобиля с водителем и выясним факторы, которые могут повлиять на ежедневный пробег таксистов, предлагающих данный вид услуги.

Множественный регрессионный анализ

Самым важным фактором является стоимость проезда (цена, взимаемая за километр пути).

Другие потенциальные факторы являются детерминантами спроса, включая цену заменителей, то есть цену общественного транспорта или конкурирующих услуг такси независимо от того, рабочий или выходной день, ясная или дождливая погода и так далее.

Один из методов создания функции спроса заключается в использовании множественного регрессионного анализа для выяснения взаимосвязи между требуемым количеством, ценой продукта и всеми другими факторами.

Множественный регрессионный анализ присваивает различные коэффициенты каждому из факторов, влияющих на спрос. Знак коэффициента — положительный или отрицательный — говорит нам, связаны ли спрос и фактор положительно или отрицательно.

Предположим для упрощения, что вы использовали только две переменные — (1) цену самого продукта и (2) рост цены конкурирующего общественного транспорта — и пришли к следующему уравнению:

Q = 1,200,000 – 150,000 × P + 200,000 × P_PT, где

Q — это потребляемые километры,

P — цена за километр услуги по вызову пассажиров,

P_PT — увеличение цены за поездку в системе общественного транспорта.

Параметр Р имеет отрицательный знак, который показывает, что с каждым долларовым увеличением стоимости проезда за километр требуемое количество будет уменьшаться на 150 000 километров в день.

С другой стороны, параметр P_PT имеет положительный знак, а это означает, что увеличение платы за проезд в общественном транспорте на один доллар приведет к увеличению спроса на 200 000 километров.

Поскольку приведенное выше уравнение создает связь не только между требуемыми километрами и взимаемой ценой, но и с ценой заменителя, оно представляет собой как сдвиг кривой спроса, так и движение вдоль кривой спроса.

До тех пор, пока цены на общественный транспорт не изменятся, мы можем упростить функцию спроса до соотношения между Q и P:

Q = 1,200,000 – 150,000 × P

Мы можем разработать график спроса, используя приведенное выше уравнение, просто подключив различные цены за километр.

Обратная функция спроса

График спроса и предложения обычно строится таким образом, что количество находится на оси X, а цена — на оси Y, но функция спроса, которую мы определили выше, имеет цену (P) как независимую переменную и количество (Q) как независимую переменную.

Функция спроса иногда определяется ценой P как независимой переменной. Такая функция спроса называется обратной функцией спроса.

С помощью всего лишь нескольких математических манипуляций мы можем преобразовать функцию спроса, определенную выше, в обратную функцию спроса:

150,000 × P = 1,200,000 – Q

P = (1,200,000 – Q) / 150,000

P = 8 – Q / 150,000

Обратная функция спроса полезна, когда мы заинтересованы в поиске предельного дохода, дополнительного дохода, полученного от одной проданной дополнительной единицы.

Функция предельного дохода является первой производной от обратной функции спроса. Для обратной функции спроса вида P = a — bQ функция предельного дохода равна MR = a — 2bQ. Функция предельного дохода в данном случае выглядит следующим образом:

P = 8 – 2 × Q / 150,000 = 8 – Q / 75,000

Примеры и графики

Давайте выясним, каков объем перевозок в километрах будет востребован при следующих сценариях: (A) средняя цена за километр (Р) составляет $ 1.5 и $ 1.75; и (B) средняя цена за километр (Р) составляет $ 1.5, а рост цен на общественный транспорт (Р_РТ) — $ 0.25

Сценарий А

Следующее уравнение показывает требуемое количество, соответствующее каждой цене:

Q_1.50 = 1,200,000 – 150,000 × $ 1.50 = 975,000

Q_1.75 = 1,200,000 – 150,000 × $ 1.75 = 937,500

Сценарий В

В этом случае происходит изменение цены заменителя, поэтому она представляет собой сдвиг кривой:

Q_1.50;0.25 = 1,200,000 – 150,000 × $ 1.50 + 200,000 × $ 0.25 = 1,025,000

В нашем примере Q_1.50;0.25 выше, чем Q_1.50, потому что рост цен на общественный транспорт вызвал внешний сдвиг кривой спроса.

На следующей диаграмме показано движение вдоль начальной кривой спроса в сценарии А и сдвиг в случае сценария B:

Источник

Каковы способы задания функции спроса

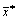
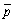
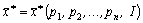
Решение задачи потребительского выбора называется точкой спроса. Она зависит от цен и дохода I и является функцией цен и дохода, т.е. функцией спроса. С другой стороны, функция спроса представляет вектор-функцию вида

Таким образом, функция спроса представляет набор n функций, каждая из которых зависит от n + 1 аргумента:

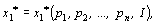
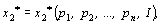
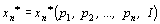
Эти функции называются функциями спроса соответствующих товаров.

Пример 1. Для набора из двух товаров на рынке, известных ценах на них p ₁ , p ₂ , доходе I найти функции спроса, если функция полезности вида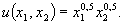

Решение. Дифференцируя функцию полезности, получим

,

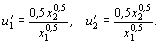
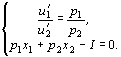
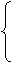
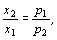
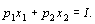
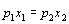
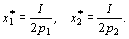
Из первого уравнения следует, что затраты денежных средств на оба товара должны быть одинаковыми, так как . Из второго уравнения получаем, что функции спроса

Таким образом, расход на каждый товар составляет половину дохода потребителя, а количество приобретенного товара равно затраченной на него сумме, поделенной на цену товара.

Модель потребительского спроса с функцией полезности мультипликативного вида

(1)

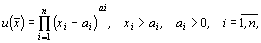
где a_i — минимально необходимое количество i — го товара.

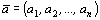
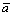
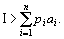
Набор товаров можно рассматривать в качестве минимальной корзины потребления. Для приобретения минимального набора необходимо, чтобы доход был больше стоимости этого набора, т.е.

(2)

Показатели степеней a_i > 0 в (1) характеризуют относительную «ценность» соответствующих товаров для потребителя.

Добавив к функции (1) бюджетные ограничения, получим задачу потребительского выбора, которую называют моделью Р. Стоуна. Приравняв к нулю частные производные функции Лагранжа L по всем переменным, получим систему n + 1 уравнений:

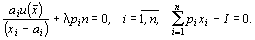
Из соотношений получаем выражения для неизвестных x_i :

(3)

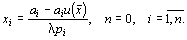
Умножим каждое из уравнений (3) на l p_i и просуммируем по i , получим

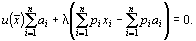
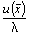
будет иметь вид

(4)

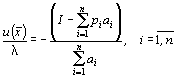
Подставляя это выражение в (2), получим в окончательном виде формулы функций спроса:

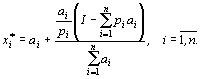
Рассмотрим частный случай модели Стоуна.

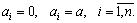
В этом случае из (4) получаем

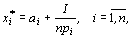
т.е. доход I делится на n равных частей и количество приобретаемого i — го товара обратно пропорционально его цене. В этом случае спрос растет при росте дохода с единичной эластичностью и уменьшается с ростом цены с эластичностью, равной минус единице.

Источник

Спрос. Функция спроса

Спрос и предложение. рыночное равновесие

1. Спрос. Функция спроса.

2. Предложение. Функция предложения.

3. Рыночное равновесие. Виды рыночного равновесия.

4. Государственное регулирование рынка.

Чтобы понять, как функционирует рынок, необходимо определить понятия «спрос» и «предложение».

Спросотражает желание и возможность покупателя приобрести определенное количество товаров (услуг) по определенной цене. Другими словами, спрос данного потребителя характеризуется не столько тем, что он хотел бы приобрести, сколько тем, что он на самом деле способен купить в данной ситуации.

Кривая (линия) спроса(D) показывает, какое количество товаров и услуг могут приобрести потребители при различных уровнях цены. Кривая спроса демонстрирует действие закона спроса: чем выше цена на товар (P) при прочих равных условиях (неценовые факторы постоянны), тем меньше объем спроса (Q_D), и наоборот.

Закон спроса не действует:

– при ажиотажном спросе, вызванном ожидаемым повышением цен;

– для некоторых редких и дорогостоящих товаров (золото, антиквариат и др.), являющихся средством вложения денег;

– при переключении спроса на более качественные и дорогостоящие товары (например, при росте дохода потребитель будет покупать вместо маргарина сливочное масло: снижение цен на маргарин не приведет к увеличению спроса на него).

Функцией спроса называется зависимость объема спроса от соответствующих факторов (ценовых и неценовых).

Функция спроса может быть представлена в виде

ценовой ф. неценовые ф.

где Q_D – объем спроса на товар;

Ps – цены на товары-заменители (субституты);

P_С – цены на дополняющие товары (комплементы);

I – доход покупателя;

M – вкусы и предпочтения покупателя;

E – ожидания потребителя;

N – количество покупателей;

В – прочие факторы.

Функцию спроса можно представить аналитическим, табличным, графическим способами.

Аналитический способ:

Линейнаяфункция спроса от ценыимеет вид

где Q_D – объем спроса; Р – цена товара;

а – точка пересечения линии спроса с осью ординат;

b – коэффициент при цене (угол наклоналинии спроса).

Нелинейная функция спроса от ценыимеет вид Q_D= k* P – n .

В случае линейной функции обратная зависимость между Р и Q_D отражается отрицательным углом наклона (-b),а в случае нелинейной функции – отрицательной степенью (-n).

Табличный способ:Например, в табл. 3.1 заданы цены на картофель в рублях и соответствующие им объемы спроса в тоннах.

Табличный способ задания функции спроса

Цена товара А (руб.)

Объем спроса (т)

Графический способ: линейная функция спроса представлена на рис. 3.1[1].

Изменение цены данного товара (P), при прочих равных условиях (неценовые факторы неизменны) влияет на объем спроса (Q_D) (то количество товара, которое потребитель готов приобрести в данный момент времени, при данных условиях), что выражается в движении вдоль кривой спроса: при уменьшении цены от P₁ до P₂ увеличивается Q_D от Q₁ до Q₂ (от т. 1 до т. 2 по кривой D) (рис. 3.1).

Изменение неценовых факторов (Ps, Pc, I, M, N, B) влияет на изменение спроса, что графически выражается смещением кривой D к D₁ (спрос вырос) или к D₂ (спрос уменьшился) (рис. 3.1).

Источник