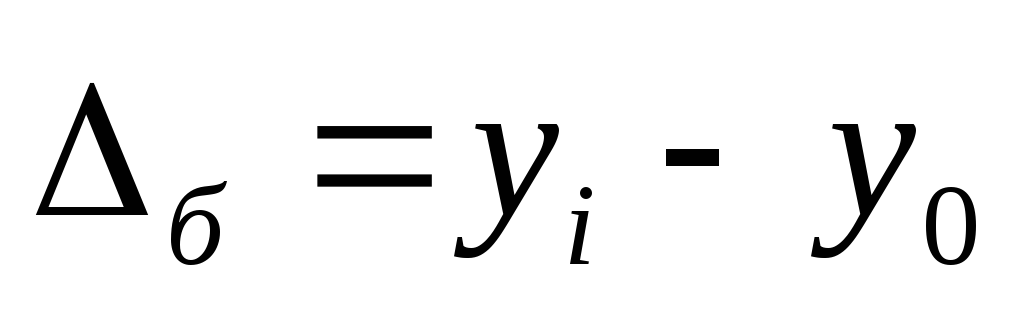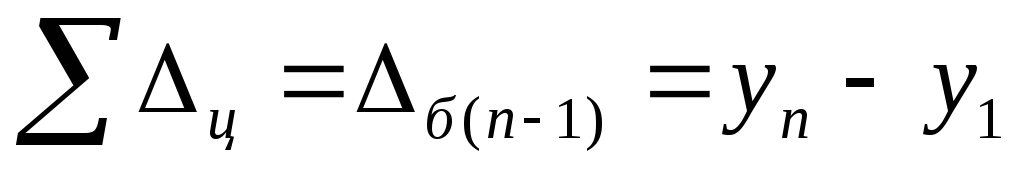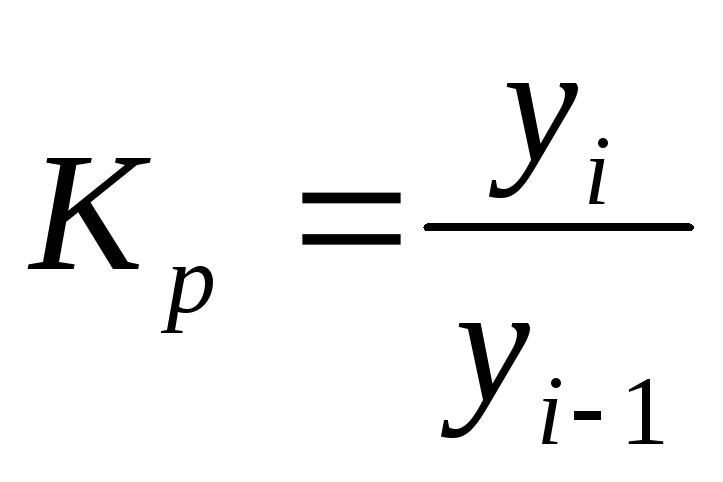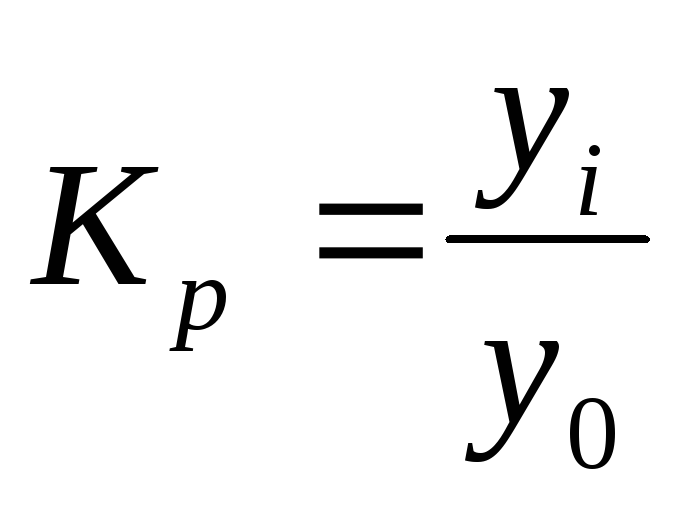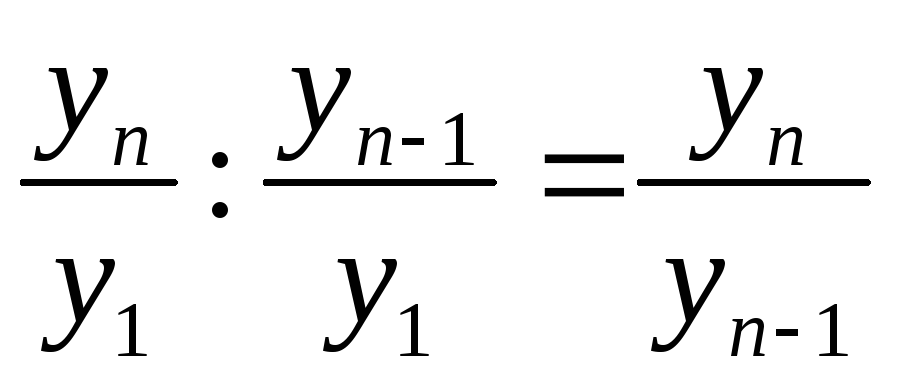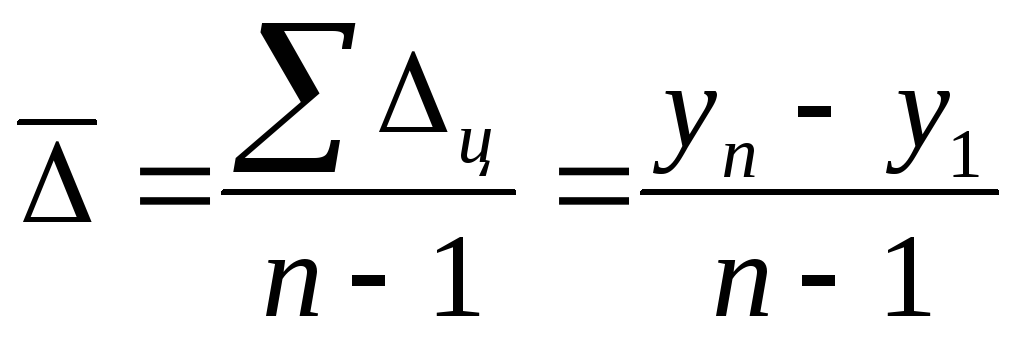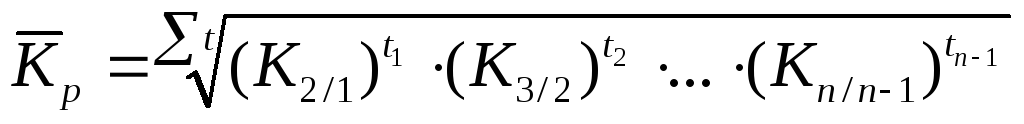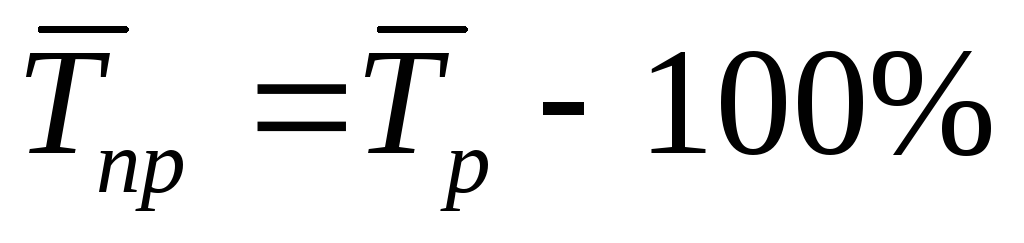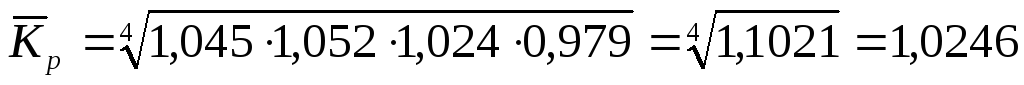Каковы способы расчета аналитических показателей ряда динамики

Аналитические показатели ряда динамики

Развитие социальных и экономических явлений во времени оценивается в статистике при помощи специальных показателей динамики:

Аналитические показатели динамики получают в результате сопоставления уровней рядов динамики. Они могут быть определены цепным и базисным способами. При цепном способе каждый уровень ряда динамики сопоставляется с предыдущим, а при базисном способе каждый уровень сопоставляется с одним и тем же уровнем, принятым за базу сравнения (как правило, первым).

К числу важнейших аналитических показателей относят:

— вес (абсолютное значение) 1 % прироста;

иногда к ним добавляют:

Абсолютный прирост показывает, на сколько (в единицах измерения уровней ряда) уровень одного периода больше или меньше уровня, принятого за базу сравнения. В зависимости от базы сравнения абсолютные приросты могут быть:

Цепной абсолютный прирост:

. (8.1)

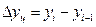
Базисный абсолютный прирост:

. (8.2)

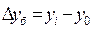
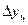
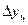
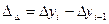
Если значения постоянны, то уровни ряда изменяются равномерно. Если же увеличиваются или уменьшаются, это означает, что развитие явления ускоряется или замедляется. Тогда имеет смысл рассчитывать показатель ускорения:

. (8.3)

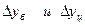
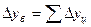
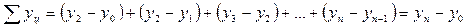
Кроме этого, между показателями существует взаимосвязь: сумма цепных абсолютных приростов равна базисному абсолютному приросту:

. (8.4)

. (8.5)

Темп роста показывает, во сколько раз данный уровень ряда динамики больше (меньше) принятого за базу сравнения. Он может выражаться в виде коэффициента либо в процентах.

Цепной темп роста:

. (8.6)

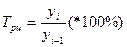
Базисный темп роста:

. (8.7)

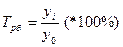
Между цепными и базисными темпами роста существует связь, которая позволяет при необходимости переходить от цепных к базисным и наоборот:

— произведение цепных темпов роста (коэффициентов) равно базисному;

— отношение базисного темпа роста (коэффициента) i-ого периода к базисному темпу роста (коэффициенту) (i — 1) –ого периода равно цепному темпу роста i-го периода.

Эта взаимосвязь в формульном виде выражается следующим образом:

, (8.8)

. (8.9)

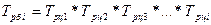
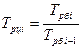
Иногда на практике приходится сравнивать темпы роста разных показателей, относящихся к одной и той же совокупности (заработная плата и производительность труда), либо одного и того же показателя, но рассчитанного в разных совокупностях (ВВП в РБ и РФ). В таких случаях производится сопоставление темпов роста двух показателей, а результат этого сопоставления называют коэффициент опережения.

Таблица 8.8 – Динамика товарооборота (данные условные)

Годы

Базисные темпы роста товарооборота по магазинам, %: — магазин 1 — магазин 2

.

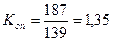
Т.е. товарооборот растет и по магазину № 1 и по магазину № 2. Однако по магазину № 2 он растет в 1,35 раза быстрее.

Темп прироста показывает, на сколько процентов данный уровень РД больше либо меньше принятого за базу сравнения. Темп прироста – это отношение абсолютного прироста к сравниваемому уровню (к базе сравнения):

— цепной темп прироста:

(8.10)

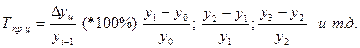
— базисный темп прироста:

(8.11)

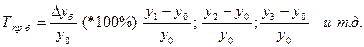
На практике темп прироста чаще всего рассчитывают исходя из взаимосвязи между показателями темпов роста и темпов прироста:

(8.12)

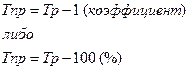
Абсолютное значение одного процента прироста (или вес 1% прироста) показывает, насколько весом каждый % прироста, какое содержание или какая абсолютная величина за ним скрывается:

(8.13)

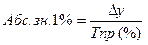
Однако можно доказать, что

(т.е. это 1/100 предыдущего уровня)

(8.14)

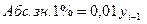
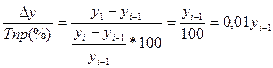
Из этого следует, что абсолютное значение 1% прироста имеет смысл лишь для цепных показателей, т.к. в случае базисных – это будет постоянное число для всех t.

Темп наращивания исчисляется как отношение цепных абсолютных приростов к уровню, принятому за базисный:

и т.д. (8.15)

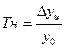
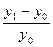
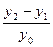
Как и ускорение, представляет интерес в том случае, если абсолютные приросты от одного периода к другому возрастают.

Таблица 8.9 – Пример расчета

Наименование показателей	Ед.изм.	Уровни показателей по годам
Прибыль	млрд. руб.
Аналитические показатели динамики:
а) абсолютный прирост: — цепной — базисный	млрд. руб.	— —
б) темп роста: — цепной — базисный	коэф-т %	— —	1,029 102,9	1,028 102,8	1,055 105,5
коэф-т %	— —	1,029 102,9	1,058 105,8	1,116 111,6
в) темп прироста: — цепной — базисный	коэф-т %	— —	0,029 2,9	0,028 2,8	0,055 5,5
коэф-т %	— —	0,029 2,9	0,058 5,8	0,116 11,6
г) абсолютное значение одного процента прироста:	млрд. руб.	—	0,069	0,071	0,073
д) темп наращивания	коэф-т	—	0,029	0,029	0,058
%	—	2,9	2,9	5,8
е) ускорение	млрд. руб.	—

Дата добавления: 2016-01-16 ; просмотров: 3273 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Аналитические показатели ряда динамики

Показатели ряда динамики можно рассчитать двумя методами: цепным и базисным. При расчете цепным методом сравнение всегда осуществляется с предыдущим уровнем (у_i-1), а базисный метод основан на сравнении с постоянным уровнемy_o. За базу берут начальный уровень ряда или другой более ранний уровень.

Абсолютный прирост(_у) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста:

Цепные и базисные абсолютные приросты взаимосвязаны:

Такая связь называется аддитивной.

Темпы (коэффициенты) ростаопределяются как отношение уровней ряда:

Если темпы роста выражены в коэффициентах, то всегда можно перейти от цепных темпов к базисным и наоборот, пользуясь двумя правилами:

а) Произведение цепных темпов роста дают базисный темп роста.

б) Частное от деления базисных темпов роста равно промежуточному цепному.

Темп роста— это коэффициент роста, выраженный в процентах:

Темп роста всегда число положительное. Если темп роста равен 100%, то значение уровня не изменилось, если больше 100%, то значение уровня повысилось, а если меньше 100% — понизилось.

Темп приростаопределяются как отношение абсолютного прироста к первоначальному уровню, и выражено в процентах:

цепной базисный

Темп прироста показывает, на сколько процентов уровень данного периода или момента времени больше (или меньше) базисного уровня:

Абсолютное значение одного процента прироста (А%) — представляет собой одну сотую часть уровня предыдущего периода и в то же время — отношение абсолютного прироста к соответствующему темпу роста:

, _.

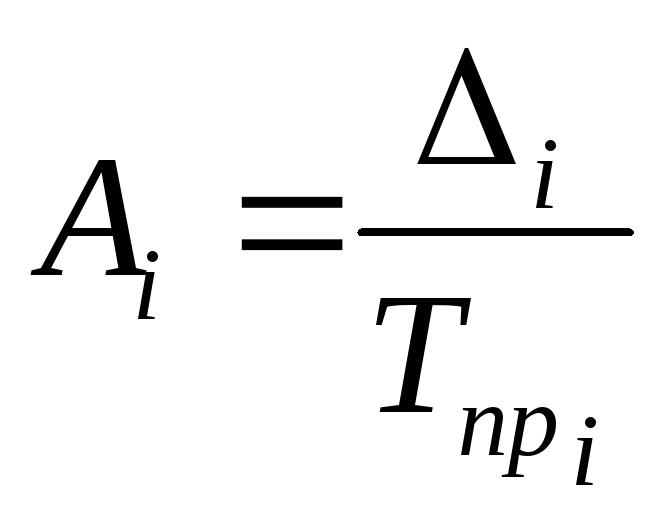
Средние показатели в рядах динамики

При анализе развития явлений часто возникает потребность дать обобщенную характеристику интенсивности развития на длительный период. Для чего используют средние показатели динамики:

1. Средний абсолютный приростнаходится по формуле:

_{где n — число периодов (уровней), включая базисный.}

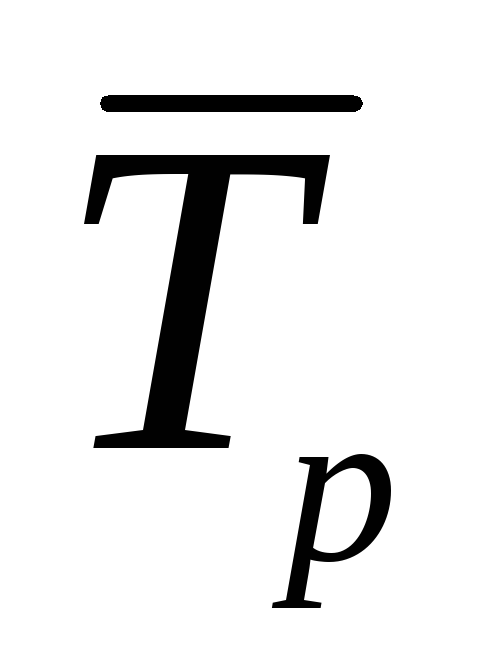
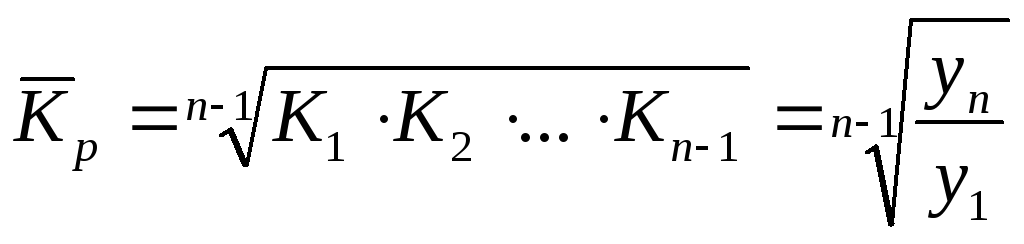
2. Средний темп роставычисляется по формуле средней геометрической простой из цепных коэффициентов роста:

, .

Когда приходится производить расчет средних темпов роста по периодам различной продолжительности (неравноотстоящие уровни), то используют среднюю геометрическую, взвешенную по продолжительности периодов. Формула средней геометрической взвешенной будет иметь вид:

где t – интервал времени, в течение которого сохраняется данный темп роста.

3. Средний темп приростане может быть определен непосредственно на основании последовательных темпов прироста или показателей среднего абсолютного прироста. Для его вычисления необходимо сначала найти средний темп роста, а затем его уменьшить на 100%:

Пример 7.1. Имеются данные о приростах объемов продаж по месяцам (в процентах к предыдущему месяцу): январь – +4,5, февраль – +5,2, март – +2,4, апрель – -2,1.

Определить темпы роста и прироста за 4 месяца и среднемесячные значения.

Решение: имеем данные о цепных темпах прироста. Преобразуем их в цепные темпы роста по формуле: Т_р = Т_р+ 100%.

Получим следующие значения: 104,5; 105,2; 102,4; 97,9

Для расчётов используются только коэффициенты роста: 1,045; 1,052; 1,024; 0,979.

Произведение цепных коэффициентов роста дают базисный темп роста.

К = 1,045·1,052·1,024·0,979 = 1,1021

Темп роста за 4 месяца Т_р= 1,1021·100= 110,21%

Темп прироста за 4 месяца Т_пр = 110,21 – 100 = +10,21%

Средний темп роста находим по формуле средней геометрической простой:

Средний темп роста за 4 месяца 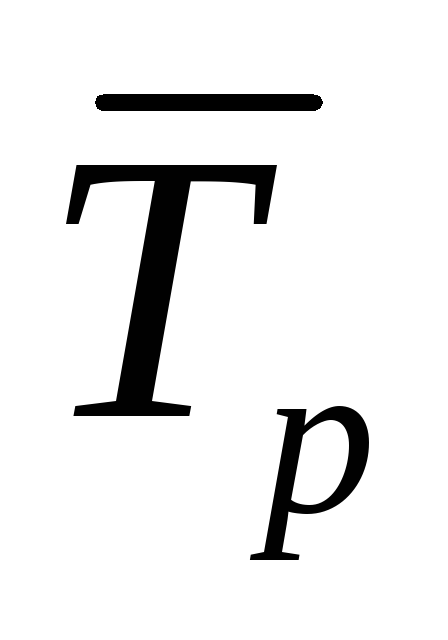= 1,0246·100= 102,46%

Средний темп прироста за 4 месяца 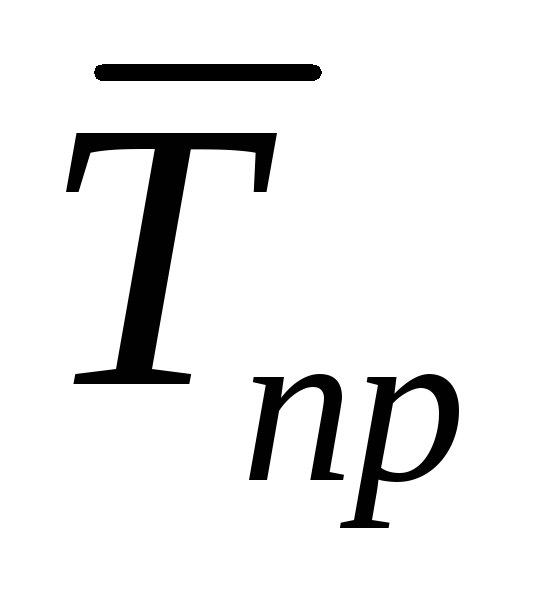= 102,46 – 100 = +2,46%

4. Средний уровень интервального ряда находится по формуле средней арифметической простой, если интервалы равны, или по средней арифметической взвешенной, если интервалы не равны:

, .

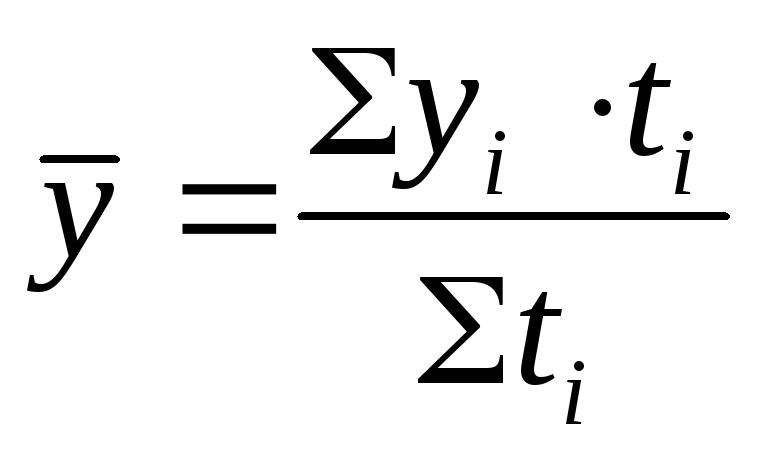
где t — длительность интервала времени.

5. Средний уровень моментного ряда динамикитак исчислить нельзя, так как отдельные уровни содержат элементы повторного счета.

а) Средний уровень моментного равноотстоящего рядадинамики находится по формуле средней хронологической:

.

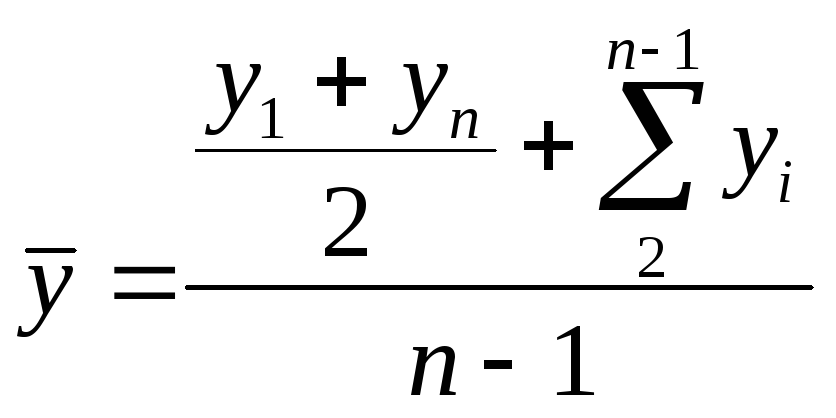
где у₁иу_n— значения уровней на начало и конец периода (квартала, года).

б) Средний уровень моментных рядов динамики с неравноотстоящими уровнямиопределяется по формуле средней хронологической взвешенной:

.

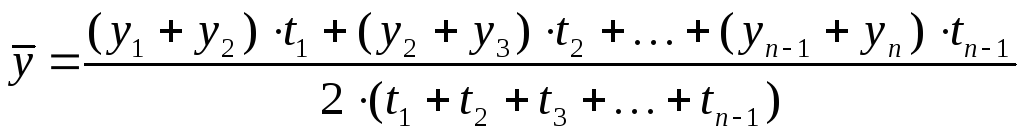
где t— длительность периода между смежными уровнями.

Пример 7.2. Имеются следующие данные об объёмах производства продукции за первый квартал (тыс.шт.) — январь — 67, февраль – 35, март – 59. Определить среднемесячный объем производства за 1 квартал.

Решение: по условию задачи имеем интервальный ряд динамики с равными периодами. Среднемесячный объем производства находится по формуле средней арифметической простой:

тыс.шт.

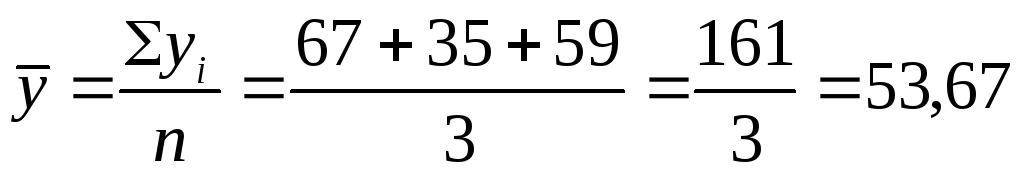
Пример 7.3. Имеются следующие данные об объёмах производства продукции за первое полугодие (тыс.т.) — среднемесячный объем за 1 квартал — 42, апрель – 35, май – 59, июнь – 61. Определить среднемесячный объем производства за полугодие.

Решение: по условию задачи имеем интервальный ряд динамики с неравными периодами. Среднемесячный объем производства находится по формуле средней арифметической взвешенной:

тыс.т.

Пример 7.4. Имеются следующие данные об остатках товаров на складе, млн. руб.: 1.01 – 17; на 1.02 – 35; на 1.03 – 59; на 1.04 – 61.

Определить среднемесячный остаток сырья и материалов на складе предприятия за Iквартал.

Решение: По условию задачи имеем моментный ряд динамики с равноотстоящими уровнями, поэтому средний уровень ряда будет исчислен по формуле средней хронологической:

млн.руб.

Пример 7.5. Имеются следующие данные об остатках товаров на складе, млн. руб.: 1.01.11 – 17; на 1.05 – 35; на 1.08 – 59; на 1.10 – 61, на 1.01.12 – 22.

Определить среднемесячный остаток сырья и материалов на складе предприятия за год.

Решение: По условию задачи имеем моментный ряд динамики с неравноотстоящими уровнями, поэтому средний уровень ряда будет исчислен по формуле средней хронологической взвешенной:

млн.руб.

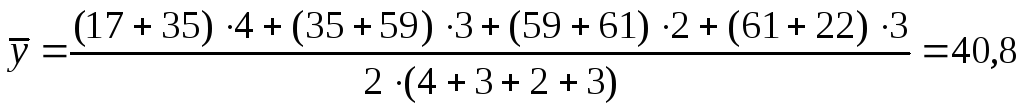
Источник