iSopromat.ru
Порядок решения задач и контрольных работ раздела «Статика» по теормеху, чаще всего сводится к определению некоторых сил, действующих на твердое тело, находящееся в равновесии.
Можно отметить следующую последовательность выполнения этапов решения задач:
- выделяется тело, равновесие которого рассматривается;
- показываются все действующие на это тело внешние (активные) силы;
- действие связей заменяется реакциями связей (пассивными силами);
- в выбранной системе координат составляются уравнения равновесия, из которых находятся искомые величины.
Успех при решении задач часто зависит от аккуратно выполненного чертежа, на котором выдержано геометрическое подобие рассматриваемых тел, верно расставленных внешних сил и реакций связей.
Неверно замененная силой связь ведет к неправильно составленным уравнениям равновесия.
В разделе «Статика» решаются статически определимые задачи, в которых число неизвестных должно соответствовать числу уравнений, которые можно составить.
Если число неизвестных оказывается больше (или меньше), то нужно проверить, верно ли заменена связь своей реакцией.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Аналитический метод решения
При аналитическом методе решения отправляются не от условия задачи, как это делают при синтетическом методе, а от ее требования, вопроса. Это характерно для всех разновидностей аналитического метода, применяемых при решении задач.
Решение задач аналитическим методом начинается с постановки следующего вопроса, связанного с требованием решаемой задачи: «Что нужно знать, чтобы ответить на вопрос данной задачи (выполнить требование)?» Для правильного ответа на поставленный вопрос необходимо знать данные задачи и учитывать те зависимости, которые связывают их с искомым числом.
Пусть для вычисления искомого Y основной задачи требуется знать, например, числа p1 и q1, из которых при помощи некоторого математического действия можно получить Y, т.е. решить основную задачу. Итак, основная задача с требованием Y преобразовалась в первую серию вспомогательных задач с искомыми p1 и q1. Обозначим первую серию вспомогательных задач через В1. Ставим тот же вопрос к каждой из вспомогательных задач: «Что нужно знать, чтобы найти p1 (q1)?» и опять при ответе на этот вопрос используем условие А основной задачи, а также арсенал математической теории.
Пусть для вычисления p1 нужно знать p2 и q2, а для вычисления q1 – знать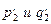 
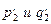
. Теперь основная задача преобразовалась во вторую серию (В2) вспомогательных задач, включающих задачи по нахождению p2, q2, .
Продолжая процесс преобразования, получаем, наконец, такую серию (Вn) вспомогательных задач, искомые которых содержатся во множестве данных основной задачи.
Итак основная задача решена аналитическим методом, поскольку этим методом проведен поиск и найден путь решения задачи; главное здесь именно в этом, а не в оформлении записи уже известного решения.
Найденное аналитическое решение можно изложить различными способами, в том числе и синтетическим. В последнем случае пришлось бы следовать от конца аналитического рассуждения к его началу, не производя при этом никаких поисков.
Если основную задачу условно записать формулой А 
У, описанный выше аналитический путь преобразования задачи изобразится схемой:
,
Где А Вn, Вn Bn-1, . . . , В1 У, откуда А У.
К рассмотренной в предыдущем пункте текстовой задаче применим аналитический метод решения. Наличие двух искомых в задаче несколько осложняет построение рассуждений, поэтому можно ограничиться сначала одним искомым, найти его и затем воспользоваться им как уже известным числом при отыскании пути получения второго искомого. Рассмотрим схему:
- За сколько часов может выполнить всю работу, работая отдельно, та машина, которая продолжила работу?
- Часть всей работы, выполненная этой машиной.
- Сколько часов работала эта машина отдельно когда она работала отдельно
- Объем всей работы
- Часть всей работы, выполненная двумя машинами совместно
- За сколько часов машины вместе Выполнят всю работу?
- Сколько часов они работали совместно?
Такой поиск обычно проводится устно и завершается составлением плана решения. Аналогично теперь можно построить схему аналитического поиска второго числа основной задачи (сделайте самостоятельно!).
В практике решения задач методы анализа и синтеза полностью разделить, изолировать друг от друга невозможно. Они полезно сочетаются. При аналитическом методе имеют место скрытые элементы синтеза. Например, преобразуя требование основной задачи в требования первой серии вспомогательных задач, мы неявно проверяем правильность этого преобразования, возможность синтезирования из искомых чисел задач первой серии искомого основной задачи.
Широкое применение находит аналитический метод при решении геометрических задач на вычисление. Здесь удобно начинать решение с соответствующей формулы, которая и показывает, какой будет первая серия вспомогательных задач и т.д. Кратко продемонстрируем это на примере следующей геометрической задачи.
Задача. В конус вписана пирамида, основанием которой служит прямоугольный треугольник и боковая грань которой, проходящая через один из катетов основания, образует с плоскостью основания двугранный угол α. Найти объем пирамиды, если образующая конуса равна l и наклонена к плоскости основания под углом β.
Р е ш е н и е. Начертим конус с вписанной в него пирамидой МАВС, в которой длины боковых ребер МА = МВ = МС = l, АС – гипотенуза треугольника АВС, центр основания конуса – точка О, Ао = ОС, ÐМАО=β, ÐМDО = α.
Формула объема пирамиды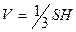 
. Задача сводится к нахождению площади основания S и высоты H = MO. (Первая серия из двух вспомогательных задач; последнюю из этих задач можно решить по имеющимся данным.).
Из прямоугольного треугольника ОМА находим Н = ОМ = lsinβ.
Для нахождения площади основания надо найти длины катетов АВ и ВС. (Получаем вторую серию из двух вспомогательных задач.)
Для определения АВ достаточно найти ОD – длину средней линии треугольника АВС, а для вычисления ВС надо найти АС ( третья серия из двух вспомогательных задач; решение первой задачи уже известно):
OD = MO ctgα = l sinβ ctg α.
Для получения АС достаточно знать АО ( четвертая серия – одна задача, которую можно решить):
; 
; 
;
;
;
.
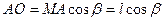
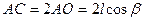
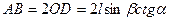
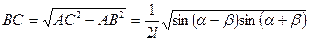
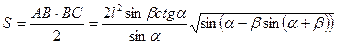
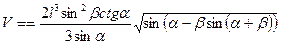
Приведенное решение является очень кратким (отсутствуют выкладки, обоснования), чтобы выделить метод решения. Учащиеся, чтобы научиться решать задачи, должны делать полные математические выкладки и уметь обосновывать каждый свой шаг в процессе решения ссылкой на условие задачи или изученную математическую теорию.
Хотя путь поиска на основе аналитического метода решения не всегда однозначен, однако он все же менее многозначен и более определен, чем путь поиска при синтетическом методе решения. Аналитический метод удобен для поиска пути решения новой для учащихся задачи, он опирается на определенное умение школьника рассуждать и эффективно способствует развитию его продуктивного, логического и функционального мышления. В результате систематического применения аналитического метода решения задач у учащихся быстрее формируется умение cамостоятельно решать новые для них задачи, чем при пользовании синтетическим методом.
Источник
Способы решения задач по механике
« Способы решения задач
Учитель первой квалификационной категории Путренкова А.А.
Законом об образовании предусмотрена существенная реорганизация всей системы школьного образования, в том числе и физического. Ориентация учебно-воспитательного процесса на удовлетворение потребностей, интересов и способностей школьников потребовала дифференциации среднего образования. Созданный в настоящее время пакет программ обеспечивает различные варианты осуществления как уровневой дифференциации в рамках многоуровневых программ и учебников, так и профильной дифференциации, подразумевающей создание специальных классов и школ с различными уклонами: гуманитарным, естественно-научным, физико-математическим и др.
И во всех программах особое внимание уделяется методике решения задач, которые являются важнейшим способом развития мышления и закрепления знаний, более широкого использования математических знаний.
Однако многие учащиеся постоянно испытывают определенные трудности в решении задач. Это особенно проявляется в начале изучения механики в 9 классе.
В настоящей разработке элективного курса рассматриваются различные методы решения задач, с помощью которых эти трудности в какой-то степени могут быть преодолены.
ЗАДАЧИ курса по выбору «Способы решения задач по механике»:
— углубить знания учащихся по физике, научить их методически правильно и практически эффективно решать задачи.
— дать учащимся возможность реализовать и развить свой интерес к физике.
— предоставить учащимся возможность уточнить собственную готовность и способность осваивать в дальнейшем программу физики на повышенном уровне.
— создать учащимся условия для подготовки к ЕГЭ по физике, для поступления в класс физико-математического профиля.
Физика всегда считалась наукой естественной, причем фундаментальной. Она раньше других естественных наук вышла на уровень количественной теории. А ее строгий язык описания позволяет получить максимально емкое и точное знание об объекте исследования.
В настоящее время общепринято, что именно такое знание позволяет создать материальные основы нашей цивилизации. Логика школьного курса физики требует, чтобы его изучение начиналось с механики.
Это обусловлено, в первую очередь, следующими причинами: из всех форм движения материи механическое движение наиболее наглядно; в классической физике моделирование физических явлений связано с созданием преимущественно механических образов структуры физических и происходящих в них процессов.
Механика — составная часть как классической, так и современной физики. Некоторые понятия механики (например, масса, импульс, энергия) используются и при описании микромира.
Учебная цель решения задач по кинематике состоит в том, чтобы помочь учащимся овладеть основными понятиями, усвоить кинематические законы движения и научиться применять их в конкретных ситуациях.
Изучение механики на векторной основе позволяет обучить учащихся координатному методу решения задач. Универсальность этого метода, общего для всех задач, независимо от характера движения тел, доказывает его преимущества. Однако эти преимущества проявляются лишь тогда, когда учащиеся овладеют этим методом.
Законы динамики — наиболее существенная часть механики. Классическая механика Ньютона — это, по существу, законы динамики, составляющие ядро ее теории. Отсюда вытекает образовательное значение изучения законов динамики.
Изучение в средней школе законов сохранения имеет огромное познавательное и мировоззренческое значение. В законах сохранения отражаются принцип материи и движения, взаимосвязь и взаимные превращения различных форм движения материи.
Законы сохранения принадлежат к наиболее общим законам природы. В отличие, например, от закона Паскаля, который справедлив лишь для жидкостей и газов, закона Ома, также имеющего ограниченную область применения, и других подобных законов, законы сохранения энергии и импульса выполняются во всех известных на сегодня физических процессах.
Поэтому изучение законов сохранения в курсе физики позволяет устанавливать внутри предметные связи.
В результате прохождения курса учащиеся должны
— чем отличается задача от других видов заданий;
— иметь представление о значении задач в жизни, науке, технике;
— основные приемы составления и решения задач;
— последовательность действий при анализе и решении задачи;
-классифицировать задачу по трем-четырем основаниям;
— анализировать физическое явление;
— проговаривать вслух решения;
— анализировать полученный ответ;
— подбирать и составлять задачи на тему.
-решать расчетные и графические задачи на применение уравнения равномерного и равноускоренного движения и движения по окружности;
-решать задачи на применение второго закона Ньютона в случае движения тела под действием нескольких сил;
-применять законы сохранения механики для решения кинематических и динамических задач.
В итоге прохождения курса школьники должны выйти на теоретический уровень решения задач: решение по определенному плану, владение основными приемами решения, осознание деятельности по решению задачи, самоконтроль и самооценка, моделирование физических явлений.
При решении задач по механике должно быть сформировано:
— умение решать задачи, накопление опыта решения задач различной трудности,
— общая точка зрения на решение задачи как на описание того или иного физического явления физическими законами.
данного элективного курса заключаются в следующем:
— ознакомить учащихся с наиболее общими приемами и методами решения типовых задач по механике
— научить применять теоретические знания и физические законы при решении задач;
— научить определять координаты движущегося тела;
— описывать движение различными способами: графическим и координатным (как функции от времени);
— читать и строить графики, выражающие зависимость кинематических величин от времени при равномерном и равноускоренном движениях;
— научить решать задачи на совместное движение нескольких тел;
— совершенствовать навыки решения качественных задач, поскольку решение таких задач часто вызывает у школьников затруднения.
С целью расширения кругозора и развития коммуникативных способностей учащихся использовать такие формы обучения как лекция, доклады, урок-игра.
Источник
