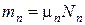Какими способами можно задать состав газовой смеси

Способы задания состава смеси

В технике часто имеют дело с газовыми смесями, близкими по свойствам с идеальными газами. Такие газы представляют механическую смесь отдельных газов. Примером газовой смеси может служить воздух, который состоит из кислорода, углекислого газа, водяных паров и одноатомных газов. Поэтому, для решения практических задач необходимо уметь определять основные параметры газовой смеси: газовую постоянную, среднюю молекулярную массу, парциальные давления и др.

Под газовой смесью понимается система, состоящая из нескольких газов, не вступающих между собой в химические реакции. Каждый газ в смеси независимо от других газов полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объем смеси. Молекулы газа создают давление на стенки сосуда, которое называется парциальным (частичным). При этом считается, что каждый газ, входящий в газовую смесь, подчиняется уравнению состояния Клапейрона, т.е. он является идеальным газом. Газовая смесь идеальных газов подчиняется закону Дальтона — общее давление смеси газов равно сумме парциальных давлений отдельных газов, составляющих газовую смесь:

p = p₁ + p₂ +…+ p_n = 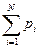, (2.1)

Парциальное давление — это давление, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же объеме и при той же температуре, что и в смеси.

Параметры газовой смеси могут быть вычислены по уравнению Клапейрона

,

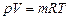
где все величины, входящие в уравнение, относятся к газовой смеси.

Задачей расчета является определение при заданном составе смеси средней молекулярной массы, или газовой постоянной смеси, после чего получение всех остальных параметров можно произвести по уравнению состояния для смеси.

Газовая смесь может быть задана массовыми, объемными и мольными долями.

Массовой долей (массовой концентрацией) называется отношение массы каждого газа к общей массе смеси.

, доли ед.; кг; ,

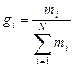
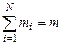
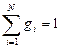
где g_i — массовая доля i-го газа; m_i — масса i-го газа, кг; m — масса газовой смеси, кг; i = 1, 2, …, N — число компонентов составляющих газовую смесь.

Объемной долей (объемной концентрацией) называется от-

ношение парциального (приведенного) объема каждого газа к общему объему смеси газов:

доли ед.; м 3 ; ,

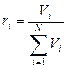
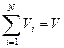
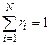
где r_i — объемная доля концентрация i-го газа; V_i — парциальный объем i-го газа, м 3 ; V — объем, занимаемый газовой смесью, м 3 .

Парциальным объемом называется объем, который занимал бы этот газ, если бы его давление и температура равнялись давлению и температуре смеси газов.

Парциальный объем каждого газа можно определить по закону Бойля-Мариотта. При постоянной температуре будем иметь:

м 3 .

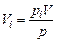
Задание смеси мольными долями равнозначно заданию ее объемными долями. Мольной долей называется отношение числа киломолей каждого газа М_i к числу киломолей газовой смеси М. Так как объемы 1 кмоля различных газов при одинаковых давлениях и температуре равны, то

,

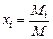
где x_i — мольная доля (мольная концентрация) i-го газа.

Мольная масса газа есть масса, численно равна молекулярной массе, отнесенной к 1 киломолю газа

[кг/кмоль].

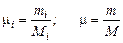
Мольные доли будут равны

доли ед.

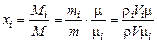
Для плотности газа можно написать

[кг/м 3 ]. .

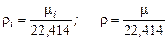
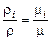
Подставив соотношение плотностей в выражение для мольной концентрации, будем иметь

.

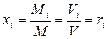
Источник

Газовые смеси. Способы их задания. Закон Дальтона.

В практике чаще приходиться встречаться не с чистыми газами, а с их механическими смесями; одной из самых важных смесей является воздух, представляющий собой смесь азота и кислорода, с небольшой примесью аргона, углекислоты и водяного пара. Большое значение имеют такие газовые смеси, как природный газ (метан и другие углеводороды), продукты сгорания топлив (диоксид углерода, азот, водяной пар и т.п.).

Под газовой смесью понимается смесь отдельных газов, не вступающих между собой ни в какие химические реакции. Каждый газ (компонент) в смеси независимо от других газов полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объём смеси.

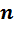
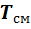
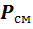
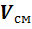
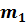
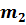
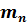
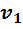
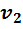
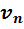
Для проведения расчетов с газовыми смесями необходимо установить параметры, характеризующие их состояние. Пусть имеется смесь из идеальных газов. Температура газовой смеси , давление её , объём ; массы газов, находящихся в смеси, равны соответственно , . ; количества веществ отдельных компонентов смеси , , …. , .

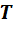
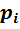
Если смесь находится в равновесии, то, несомненно, температура всех газов одинакова и равна температуре смеси cм. В равновесном состоянии молекулы каждого газа рассеяны равномерно по всему объёму смеси, т.е. имеют свою определенную концентрацию и, следовательно, свое давление , называемое парциальным.

Парциальное давление – это давление, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же объёме и при той же температуре, что и в смеси.

Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в неё компонентов:

(16)

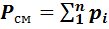
Этот закон был установлен Дальтоном в 1801 г.

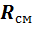
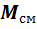
Все зависимости, полученные для идеальных газов, справедливы и для их смесей, если в них подставить газовую постоянную ( ) и молекулярную (молярную) массу ( ).

Очевидно, что масса газовой смеси равна сумме отдельных компонентов:

(17)

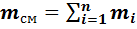
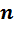
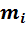
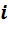
где : — число компонентов смеси;

— масса -го компонента.

Качественный состав газовой смеси может быть задан различными способами.

Источник

ЛЕКЦИЯ 3. Способы задания состава смеси

Способы задания состава смеси. Соотношения между ними

Смеси идеальных газов. Закон Дальтона

В ТТД чистым веществом наз. вещество, все молекулы которого одинаковы. Смесь, состоящая из нескольких чистых веществ наз. раствором. Чистыми веществами явл., например, вода, этиловый спирт, азот, аммиак и т.п. Чистые вещества, составляющие смесь, наз. компонентами.

При рассмотрении смесей газов исходят из того, что смесь идеальных газов, не вступающих в химическое взаимодействие друг с другом, так же явл. идеальным газом и подчиняется таким же законам. При этом каждый газ, входящий в состав газовой смеси, ведет себя так, как будто он один при данной температуре Т занимает весь объём смеси, т.е. равномерно распространяется по всему объёму смеси и оказывает на стенки сосуда своё давление, наз. парциальным.

В 1801г. английский учёный Дальтон экспериментально установил связь между парци- альными давлениями отдельных газов и давлением смеси. При постоянной температуре полное давление смеси нескольких газов равно сумме их парциальных давлений:

, (2.21)

где p_і— парциальное давление i-го газа; n-количество газов, составляющих газовую смесь.

Газовая смесь может быть задана массовыми, объёмными и мольными долями.

Газовая смесь, заданная массовым составом, характеризуется массовыми долями. Массовой долей компонента g_i наз. отношение массы отдельного компонента m_i, входящего в смесь, к массе всей смеси М_см, т.е.

, (2.22)

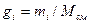
Очевидно, что масса газовой смеси равна сумме масс всех входящих в неё газов:

(2.23)

Определим сумму массовых долей отдельных газов:

, (2.24)

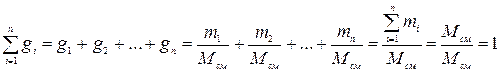
Массовые доли часто задаются в процентах (%).

Газовая смесь, заданная объёмным составом, характеризуется объемными долями (r_i). Объёмная доля каждого газа выражается отношением приведенного объёма газа V_i к полному объёму смеси V_см.

, (2.25)

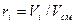
Приведенным V_i наз. объём, который занимал бы компонент газа, если бы его давление р_i и температура Т_i равнялись давлению р_см и температуре Т_см.

Парциальный объём каждого газа определяется по закону Бойля-Мариотта. При T=const.=T_см

, (2.26)

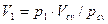
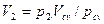
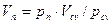
Из уравнений (2.26) имеем: ; ; … , (2.27)

Сложив отдельно левые и правые части уравнений (2.27), получим:

, (2.28)

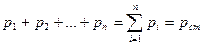
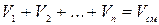
По закону Дальтона , следовательно

, (2.29) То есть сумма парциальных объёмов газа,

составляющих смесь, равна объёму смеси газов (закон Амала).

Сумма объёмных долей газов, составляющих смесь, равна единице

, (2.30)

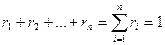
Объёмные доли часто задаются в процентах (%).

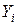
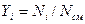
Газовая смесь, заданная мольным составом, характеризуется мольными долями. Мольной долей наз. отношение количества молей N_i рассматриваемого компонента к общему количеству молей смеси N_i. , (2.31)

Вполне очевидно, что сумма молей всех газов, составляющих смесь, равна общему числу молей газовой смеси, т.е. 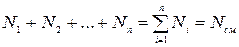, (2.32)

Сумма мольных долей смеси газов равна единице: 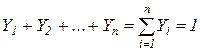, (2.33)

Если известен массовый состав смеси, то по нему можно найти её мольный состав. Массы отдельных газов m_i и полную массу смеси М_см можно выразить через число молей следующем образом: ; ; …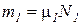

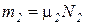
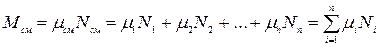
, (2.34)

2.8. Теплоёмкость. Массовая, объёмная и молярная теплоемкости.

Теплоемкости при постоянных объёме и давлении

Теплоёмкостью наз. количество теплоты, необходимое для повышения температуры тела на один градус. Теплоёмкость не является постоянной величиной и в общем случае изменяется с изменением температуры и давления. Теплоёмкость единицы количества вещества наз. удельной теплоёмкостью. Удельная теплоёмкость тела зависит от химического состава, параметров состояния рабочего тела, а также от вида процесса, в котором телу сообщается

теплота, поскольку теплота есть функция процесса. Размерность удельной теплоёмкости:

Дж/(кг(м 3 , (моль))) К).

В ТТД различают удельные массовую с, (Дж/(кг К)), объемную с’ , (Дж/(м 3 К)) и мольную с_µ (Дж/(моль К)) теплоёмкости.

Зависимости между удельными теплоёмкостями устанавливаются из следующих выражений:

; , где , (2.35)

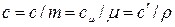
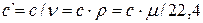
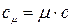
Различают истинную и среднюю теплоёмкости.

Истинной теплоёмкостьюназ. производная от количества теплоты, подведённой к телу, по температуре этого тела и определяется выражением:

, (2.36)

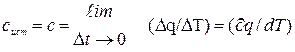
То есть истинная теплоёмкость тела – это его теплоёмкость при данной температуре.

Средней теплоёмкостью наз. теплоёмкость в интервале температур Т₂ – Т₁, она обозначается С_m. При уменьшении разности температур средняя теплоёмкость приближается к истинной.

, (2.37)

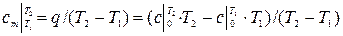
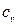
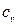
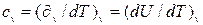
Удельной изохорной теплоемкостью наз. количество теплоты, которое необходимо подвести к рабочему телу в изохорном процессе с тем, чтобы изменить его

температуру на 1 К. , (2.38)

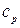
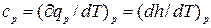
Удельной изобарной теплоемкостью наз. количество теплоты, которое необходимо подвести к рабочему телу в изобарном процессе с тем, чтобы изменить его температуру на 1 К. , (2.39)

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник