Какими способами можно задать положение точки физика 10 класс мякишев

Кинематика. Задание положения точки.

Положение точки в пространстве можно задать двумя способами: координатным и векторным.

При задании движения координатным способом с телом отсчета связывают какую-либо систему координат, например, декартовую. Движение точки М будет задано в том случае, если ее координаты будут известны, как функции времени:

Эти зависимости называются уравнениями движения точки в декартовых координатах. Они выражают текущие координаты движущейся точки в виде функций времени. Если точка движется, оставаясь все время в одной плоскости, можно ограничиться двумя уравнениями движения: x = x(t), y = y(t).

Векторный способ задания положения точки .

Допустим, М – движущаяся точка относительно тела отсчета А. В теле А в качестве точки отсчета выберем произвольную точку О и построим вектор Этот вектор называется радиус-вектором точки М.

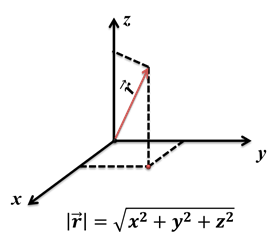
Радиус-вектор – это вектор, соединяющий начало отсчета с положением точки в любой момент времени.

Когда точка М движется, радиус-вектор непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени Зная эту функцию, для каждого времени t можно построить вектор и тем самым найти положение движущейся точки в данный момент. Функция называется векторным законом (векторным уравнением) движения точки М.

Точка задается радиус-вектором, если известны его длина (модуль) и направление в пространстве, другими словами – значения его проекций r_x, r_y, r_z на оси координат OX, OY и OZ, или углы между радиус-вектором и осями координат. При рассмотрении движения на плоскости:

Здесь за мы принимаем модуль радиус-вектора , а r_x и r_y являются его проекциями на оси координат, все три величины скалярны, x и y – координаты точки А.

Из этих уравнений видно, что между координатным и векторным способами задания положения точки существует связь.

Источник

Положение и движение точки в пространстве

Урок 2. Физика 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Положение и движение точки в пространстве»

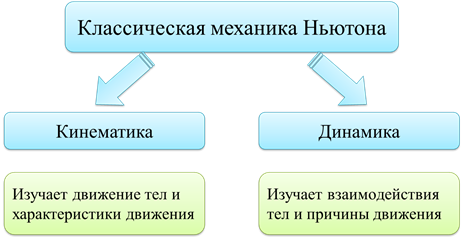
Мы продолжаем тему классической механики Ньютона. Механика делится на два основных раздела: кинематика и динамика. Мы начнём с изучения кинематики.

Кинематика изучает движение тел, способы описания этого движения, а также, его характеристики.

Описать движение человека или полет бабочки математически — это крайне сложная задача. Но есть задачи и проще: например, описать движение материальной точки. Добавим теперь, что эта точка двигается равномерно и прямолинейно. Тогда, описать её движение не так уж сложно. Именно с таких идеализированных моделей и следует начать изучение кинематики. Ведь если мы сможем описать движение каждой точки тела, то мы также сможем описать движение самого тела.

В первую очередь, нужно создать систему отсчёта. Система отсчёта состоит из тела отсчёта, системы координат и счётчика времени.

Тело отсчёта — это физическое тело, относительно которого задаётся положение данного тела или точки.

Понять это довольно просто. На рисунке изображено дерево.

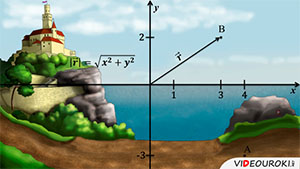
На каком расстоянии находится это дерево? На каком расстоянии от чего? — спросите вы. Конечно, нам нужно выбрать точку отсчета. Это может быть белый треугольник на камне, а может быть флажок на за́мке. В зависимости от этого выбора, ответ на вопрос будет различным. Необходимо выбрать какую-то точку за точку отсчёта, то есть за ноль. Скажем, мы можем обозначить за ноль центр картинки.

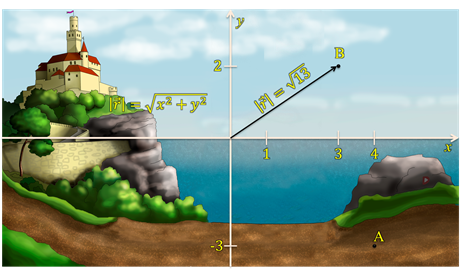
Далее, мы используем декартовы координаты, чтобы описать положения тел. Выбираем единичный отрезок и, исходя из этого определяем положения тел. Это положение задаётся с помощью координат. Например, точка А имеет координаты четыре и минус три, а точка Б — три и два. Также, можно задать положение тела с помощью радиус-вектора — это вектор, который соединяет точку и начало координат.

Радиус-вектор обозначается латинской буквой r и, как и любой другой вектор, имеет длину и направление. Длиной радиус-вектора будет является геометрическая сумма координат точки. Иными словами, мы вычисляем длину радиус-вектора, используя теорему Пифагора. То есть, длина радиус-вектора, описывающего положение точки B будет равна .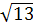

Модуль и направление любого вектора находят с помощью проекций этого вектора на оси координат.

Что же такое проекция? Давайте рассмотрим вектор 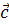с начальной точкой А и конечной точкой B, находящийся в системе координат на плоскости.

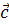
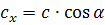
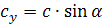
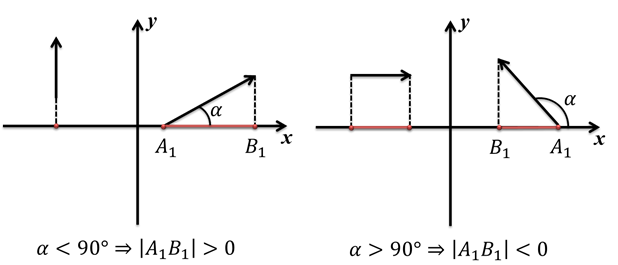
Из точек А и B опустим перпендикуляры на ось икс. Длина отрезка А₁ B₁ — это и есть проекция вектора цэ на ось x. Точно таким же способом находится проекция вектора на ось y. Как видно из построения: . Аналогично можно найти проекцию на ось y: ..

Проекция вектора на ось — это алгебраическая величина. Её знак можно определить так: если, двигаясь от начальной точки проекции до конечной точки проекции, надо идти в положительном направлении, то проекция положительная, а в противном случае — она отрицательная.

Иначе это можно объяснить так: если вектор составляет острый угол с направлением оси, на которую мы собираемся сделать проекцию, то проекция будет положительной, а если угол между вектором и направлением оси — тупой, то проекция будет отрицательной.

Нетрудно догадаться, что если вектор перпендикулярен оси, то его проекция на эту ось будет равна нулю.

Аналогично, если вектор параллелен оси, то его проекция на эту ось будет равна модулю вектора.

Рассмотрим теперь, как задать положение точки в пространстве, а не на плоскости. Как вы знаете, у есть три пространственных измерения, поэтому, чтобы задать положение точки в пространстве нам нужно три координаты. Сначала мы точно также, как и ранее, находим точку на плоскости, а потом от этой точки откладываем числовое значение координаты z параллельно оси Z.

Положение такой точки точно также можно задать с помощью радиус-вектора. Его модуль также будет находиться с помощью геометрической суммы координат точки.

Примеры решения задач.

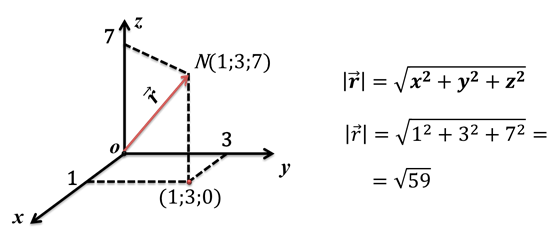
Задача 1. В системе координат отметьте точку N (1;3;7), постройте соответствующий радиус-вектор и найдите его длину.

Задача 2. В системе координат отметьте точку N (1;3;7), постройте соответствующий радиус-вектор и найдите его длину.

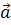
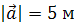
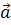
Задача 3. Постройте проекции вектора на оси x и y и найдите их числовые значения, если , а угол между и осью x составляет 30.

Источник

«Движение точки и тела. Положение точки в пространстве. Способы описания движения. Системы отсчета. Перемещение».
план-конспект урока по физике (10 класс) на тему

Цели урока: объяснить необходимость изучения механики; ввести понятия «траектория», «перемещение», «путь», «система отсчета».

Программное обеспечение: Microsoft Power Point.

I. Организационный момент.

II. Изучение нового материала.

Механическое движение – изменение с течением времени положения тела по отношению к другим телам.

ü Двигаетесь ли вы, находясь в классе? (В классе Вы находитесь относительно Земли, но движетесь вместе с ним вокруг Солнца)

Говорят, тело принимаем за материальную точку.

Материальная точка – тело, размерами и формой которого можно пренебречь в условиях данной задачи.

Если траектория прямая, движение называется прямолинейным, если кривая- криволинейным. Траектория движения указывает все положения, которые занимала точка. Но ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки .Чтобы получит полное описание, необходимо знать, в какой момент точка занимала то или ниое положение на траектории.

Скачать:

Вложение	Размер
u.2.konspekt.doc	61.5 КБ

Предварительный просмотр:

ПЛАН – КОНСПЕКТ УРОКА ПО ФИЗИКЕ В 10 КЛАССЕ

«Движение точки и тела. Положение точки в пространстве. Способы описания движения. Системы отсчета. Перемещение».

Цели урока : объяснить необходимость изучения механики; ввести понятия «траектория», «перемещение», «путь», «система отсчета».

Программное обеспечение : Microsoft Power Point.

1. Организационный момент.
2. Изучение нового материала.

Механическое движение – изменение с течением времени положения тела по отношению к другим телам.

• Двигаетесь ли вы, находясь в классе? (В классе Вы находитесь относительно Земли, но движетесь вместе с ним вокруг Солнца)

Говорят, тело принимаем за материальную точку.

Материальная точка – тело, размерами и формой которого можно пренебречь в условиях данной задачи.

Если траектория прямая, движение называется прямолинейным, если кривая- криволинейным. Траектория движения указывает все положения, которые занимала точка. Но ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки .Чтобы получит полное описание, необходимо знать, в какой момент точка занимала то или ниое положение на траектории.

Описать движение можно:

• С помощью таблиц;
• Графически;
• Аналитически.

Источник