Понятие множества

С понятием множества вы познакомились на уроках математики ещё в начальной школе, а затем работали с ним при изучении математики и информатики в основной школе.

Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое.

Примерами множеств могут служить: множество всех учеников вашего класса, множество всех жителей Санкт-Петербурга, множество всех натуральных чисел, множество всех решений некоторого уравнения и т. п.

Множества принято обозначать прописными буквами латинского алфавита (А, В, С, . ). Объекты, входящие в состав множества, называются его элементами.

Множество можно задать следующими способами:

1) перечислением всех его элементов;

2) характеристическим свойством его элементов.

В первом случае внутри фигурных скобок перечисляются все объекты, составляющие множество. Каждый объект, входящий в множество, указывается в фигурных скобках лишь один раз.

Например, запись М = <1, 3, 5, 7, 9>означает, что множество М состоит из чисел 1, 3, 5, 7 и 9. Точно такой же смысл будет иметь запись М = <3, 1, 5, 9, 7>. Иначе говоря, порядок расположения элементов в фигурных скобках значения не имеет. Важно точно указать, какие именно объекты являются элементами множества.

Например:

• число 5 является элементом множества М: 5 ∈ М1;
• число 4 не является элементом множества М: 4 ∉ М.

Это же множество можно задать с помощью характеристического свойства образующих его элементов — такого свойства, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит. В нашем примере можно говорить о множестве натуральных однозначных нечётных чисел.

В рассматриваемом множестве М содержится 5 элементов. Это обозначают так: |М| = 5. Можно составить множество, содержащее любое число элементов. Например, множество всех корней уравнения х 2 — 4х — 5 = 0 конечно (два элемента), а множество всех точек прямой бесконечно. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом ∅.

Первый способ задания множеств применим только для конечных множеств, да и то при условии, что число элементов множества невелико. Вторым способом можно задавать как конечные, так и бесконечные множества.

Из некоторых элементов множества М можно составить новое множество, например Р: Р = <1, 3, 5>.

Если каждый элемент множества Р принадлежит множеству М, то говорят, что Р есть подмножество М, и записывают: Р ⊂ М.

Само множество М является своим подмножеством, т. к. каждый элемент М принадлежит множеству М. Пустое множество также является подмножеством М.

Работая с объектами какой-то определённой природы, всегда можно выделить «самое большое» или универсальное множество, содержащее все возможные подмножества. Пусть А — множество чётных чисел, В — множество натуральных чисел, С — множество чисел, кратных пяти. Тогда самым большим множеством, содержащим в себе множества А, В и С, а также другие подобные множества, будет множество целых чисел. Универсальное множество будем обозначать буквой U.

Для наглядного изображения множеств используются круги Эйлера (рис. 4.1). Точки внутри круга считаются элементами множества.

Источник

Урок 21
§17. Некоторые сведения из теории множеств

Содержание урока:

17.1. Понятие множества
	17.2. Операции над множествами

17.1. Понятие множества

С понятием множества вы познакомились на уроках математики ещё в начальной школе, а затем работали с ним при изучении математики и информатики в основной школе.

Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое.

Примерами множеств могут служить: множество всех учеников вашего класса, множество всех жителей Санкт-Петербурга, множество всех натуральных чисел, множество всех решений некоторого уравнения и т. п.

Множества принято обозначать прописными буквами латинского алфавита (А, В, С, . ). Объекты, входящие в состав множества, называются его элементами.

Множество можно задать следующими способами:

1) перечислением всех его элементов;
2) характеристическим свойством его элементов.

В первом случае внутри фигурных скобок перечисляются все объекты, составляющие множество. Каждый объект, входящий в множество, указывается в фигурных скобках лишь один раз.

Например, запись М = <1, 3, 5, 7, 9>означает, что множество М состоит из чисел 1, 3, 5, 7 и 9. Точно такой же смысл будет иметь запись М = <3, 1, 5, 9, 7>. Иначе говоря, порядок расположения элементов в фигурных скобках значения не имеет. Важно точно указать, какие именно объекты являются элементами множества.

Например:

• число 5 является элементом множества М: 5 ∈ М 1) ;
• число 4 не является элементом множества М: 4 ∉ М.

1) Символ ∈ называется знаком принадлежности.

Это же множество можно задать с помощью характеристического свойства образующих его элементов — такого свойства, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит. В нашем примере можно говорить о множестве натуральных однозначных нечётных чисел.

В рассматриваемом множестве М содержится 5 элементов. Это обозначают так: |М| = 5. Можно составить множество, содержащее любое число элементов. Например, множество всех корней уравнения х 2 — 4х — 5 = 0 конечно (два элемента), а множество всех точек прямой бесконечно. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом ∅.

Первый способ задания множеств применим только для конечных множеств, да и то при условии, что число элементов множества невелико. Вторым способом можно задавать как конечные, так и бесконечные множества.

Из некоторых элементов множества М можно составить новое множество, например Р: Р = <1, 3, 5>.

Если каждый элемент множества Р принадлежит множеству М, то говорят, что Р есть подмножество М, и записывают: Р ⊂ М.

Само множество М является своим подмножеством, т. к. каждый элемент М принадлежит множеству М. Пустое множество также является подмножеством М.

Работая с объектами какой-то определённой природы, всегда можно выделить «самое большое» или универсальное множество, содержащее все возможные подмножества. Пусть А — множество чётных чисел, В — множество натуральных чисел, С — множество чисел, кратных пяти.

Тогда самым большим множеством, содержащим в себе множества А, В и С, а также другие подобные множества, будет множество целых чисел. Универсальное множество будем обозначать буквой U.

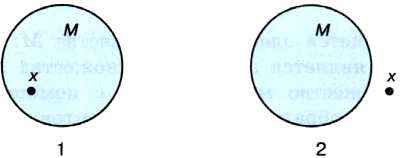
Для наглядного изображения множеств используются круги Эйлера (рис. 4.1). Точки внутри круга считаются элементами множества.

Рис. 4.1. Графическое изображение множеств: 1) х ∈ М, 2) х ∉ М

Cкачать материалы урока

Источник

Информатика. 10 класс

Конспект урока

Информатика, 10 класс. Урок № 10.

Тема — Некоторые сведения из теории множеств

Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором, создателем теории множеств.

Немецкий математик, создатель теории множеств

Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое. Под множеством мы можем понимать: учеников класса, фрукты, деревянные предметы, числа и т. д.

Множество учеников класса

Множество деревянных предметов

Множества принято обозначать прописными буквами латинского алфавита (A,B,C,D и т. д.).

Множество можно задать перечислением всех его элементов, заключенных в фигурные скобки:

Из некоторых элементов одного множества можно составить новое. Тогда такое множество Е принято называть подмножеством D:

Для наглядности множества можно изображать в виде окружности, так называемых кругов Эйлера, где элементы, входящие в множество, изображают внутри круга, а остальные вне:

Пересечением множеств называется множество их общих элементов.

Пусть множество A будет состоять из элементов 1,3,6,9,12,15, а множество B из элементов 2,4,6,8,10,12. Тогда в пересечение этих множеств будет входить 2,6,12:

Множество может не содержать элементы, тогда оно будет называться пустым.

Если множества не имеют общих элементов, то их пересечение — пустое множество:

Объединением двух множеств называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов:

Разностью множеств А и В называется множество элементов, принадлежащих множеству А, которые не принадлежат множеству В:

Если множество А является подмножеством B, то дополнением называется разность множества А и В:

Мощностью множества называется число его элементов: A=

Таким образом, мощность непересекающихся множеств будет являться суммой мощностей каждого множества:

Для вычисления мощности пересекающихся множеств можно использовать принцип включений и исключений:

Для вычисления мощности пересечения трех множеств принцип включений и исключений выглядит так:

В классе 17 пловцов, 8 борцов и 13 футболистов. Известно, что в классе 25 детей, а ребят занимающихся футболом и плаваньем — 10, борьбой и плаваньем — 3, борьбой и футболом — 2 и только один ребенок занимается всеми тремя видами спорта. Сколько детей в классе не занимаются спортом?

по формуле включения:

Таким образом, в классе 24 ребенка занимаются хотя бы одним видом спорта, ответ 1

1. Множество общих элементов двух множеств
2. Совокупность объектов произвольной природы, которая рассматривается как единое целое
3. Число элементов множества
4. Множество элементов, не входящих в подмножество
5. Множество, состоящее из всех элементов двух (или более) множеств и не содержащее никаких других элементов

Проверьте свои ответы:

1. Пересечение
2. Множество
3. Мощность
4. Дополнение
5. Объединение

Источник