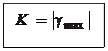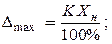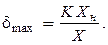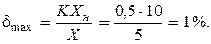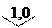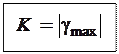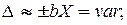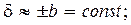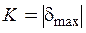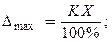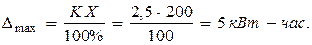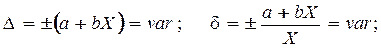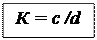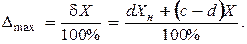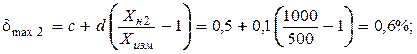Уменьшение погрешности измерений
Уменьшение систематической погрешности.
Систематическая погрешность проявляется в виде смещения Хизм относительно Х. Может быть учтена введением поправки.
При ∆с ≈ 0 – измерения правильные.
· повышение класса точности прибора;
· использование метода замещения;
· изменение знака выходной величины и др.
Уменьшение случайной погрешности.
Случайная погрешность проявляется в виде разброса значений Хизм относительно Х. Может быть оценена в виде доверительного интервала.
Способы уменьшения 
:
· повышение класса точности СИТ (при однократных измерениях);
· проведение многократных наблюдений при помощи приборов высокой чувствительности.
2.4 Классы точности
Класс точности – нормированная метрологическая характеристика средства измерения, определяемая пределами допускаемых погрешностей, а также другими свойствами, влияющими на точность.
.
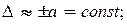
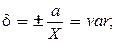
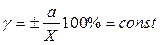
Класс точности: . Пример обозначения: 1,0
Расчетные формулы: 
Пример 1: Предел измерения амперметра 10 А, класс точности 0,5. Определить абсолютную и относительную погрешности измерения тока 5 А.
Решение:
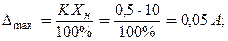
Класс точности: . Пример обозначения:
Пример 2: Определить абсолютную погрешность измерения сопротивления резистора, если показание омметра 500 Ом, а на отметке измерения 1 мм шкалы соответствует 10 Ом. Класс точности омметра
Решение:
| |
 |
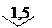
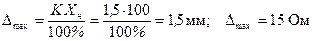
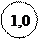Класс точности: . Пример обозначения:
Расчетная формула: 
Пример 3: Счетчик электрической энергии зарегистрировал расход энергии 200 кВт-час. Определить абсолютную погрешность измерения энергии, если класс точности счетчика .
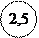
Класс точности: . Пример обозначения: 1,0/0,5 .
Допустимая погрешность
Расчетная формула: 
Пример 4 Предел измерения вольтметра 50 В, класс точности 0,5/0,2. Определить погрешность измерения напряжения 20 В.
Решение:
 |
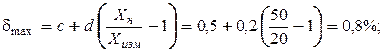
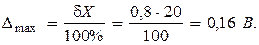Пример 5: Первый ваттметр имеет предел измерения Wн1 = 750 Bт и класс точности K1 = 0,5; второй ваттметр – соответственно Wн2 =1000 Bт и K2 = 0,5/0,1. Выбрать прибор, обеспечивающий меньшую погрешность измерения мощности 500 Вт.
 |
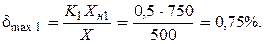Решение:
Меньшую погрешность дает второй ваттметр.
Лекция 3ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
3.1 Показатели точности измерений
Результат измерения – числовое значение, приписываемое измеряемой величине, с указанием точности измерения.
Численные показатели точности:
· доверительный интервал (доверительные границы) погрешности ΔР;
· оценка СКО погрешности S.
Правила выражения показателей точности:
· численные показатели точности выражаются в единицах измеряемой величины;
· численные показатели точности должны содержать не более двух значащих цифр;
А.Крылов: «Всякая неверная цифра – ошибка, а всякая лишняя цифра – половина ошибки»;
· наименьшие разряды значения измеряемой величины и численных показателей точности должны быть одинаковыми.
3.2 Представление результатов измерений
Результат измерения:
или
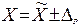
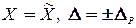
Источник
Практические приемы уменьшения погрешностей
Обычно выделяют три группы погрешностей: неустранимая погрешность; погрешность метода; вычислительная погрешность. Неустранимая погрешность порождается: а) неточностью входных данных в математическом описании задачи; б) несоответствия математической модели реальной задаче. Погрешность метода возникает из-за того, что используются приближенные методы. А погрешность вычислений возникает при вводе-выводе и при выполнении математических операций, а также при округлениях. Попробуем привести несколько практических приемов для уменьшения влияния вычислительной погрешности на результаты вычислений.
1. Сложение чисел необходимо проводить по мере их возрастания так как в машинной арифметике из-за погрешности округления существенен порядок выполнения операций.
2. В некоторых случаях имеет смысл выполнить предварительные преобразования вычисляемого выражения.
Например, вместо (a+b)^2 для случая, когда одно число намного меньше другого, лучше использовать выражение: a^2+2ab+b^2. Перемножение большого и маленького числа: 2ab позволит слегка поправить ситуацию.
3. Необходимо исключать вычитание двух почти равных чисел, тем более когда такая разность находится в знаменателе выражения.
4. Если числа равны a и b почти равны, то вычитание этих чисел следует производить раньше, чем деление или умножение.
К примеру, следует отдать предпочтение выражению (a-b)/c, а не выражению a/c-b/c. Во-первых здесь меньше операций (смотри пункт 3 и 6), а во-вторых, после деления числа станут меньше и еще меньше будут отличаться друг от друга, что может привести к обращению разности в ноль.
5. При перемножении нескольких чисел надо сразу перемножать самое большое число и самое маленькое, так как умножение друг на друга нескольких маленьких чисел может привести к появлению машинного нуля.
6. Всегда следует стремиться к уменьшению числа арифметических операций. Это объясняется тем, что чем больше операций, тем больше суммирующие погрешности.
Источник
ЛЕКЦИЯ 6. §5. Методы уменьшения погрешностей измерений
§5. Методы уменьшения погрешностей измерений.
Общим методом, пригодным в принципе для уменьшения погрешностей, является конструктивно-технологический метод, основанный на выявлении причин и источников наиболее существенных погрешностей и всемерном снижении их влияния. В конструктивно технологическом методе используются такие приемы, как термостатирование, применение малошумящих электронных компонентов, использование прецизионных элементов и узлов, материалов со стабильными характеристиками, рационального конструирования и совершенной технологии изготовления средств измерений. Однако возможности указанного метода весьма ограничены и что также очень важно, его применение с целью достижения высоких точностей измерений приводит к резкому возрастанию стоимости средств измерений. В связи с этим широкое распространение получили методы повышения точности, основанные на введении структурной и (или) временной избыточности, т. е. на введении дополнительных средств измерений (измерительных преобразователей, измерительных устройств) и (или) выполнении дополнительных измерений, результаты которых обрабатываются по специальному алгоритму, позволяющему повысить точность. Поведение систематических и случайных погрешностей во времени (при повторных измерениях) существенно различно, в связи с чем существенно отличаются и методы их уменьшения. При постоянстве значения измеряемой величины наиболее эффективным методом уменьшения случайной погрешности является усреднение результатов наблюдения. Среднее квадратическое отклонения погрешности результата измерения, т. е. среднего значения результатов n наблюдений, уменьшается до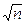 
раз.
Гораздо труднее, уменьшить случайную погрешность в том случае, когда значение измеряемой величины изменяется во времени. В этом случае используется более сложная процедура фильтрации, целью которой является получение оптимальной оценки измеряемой величины, причем оценка также рассматривается как процесс, протекающий во времени. Погрешность оценки (разность между оценкой и измеряемым процессом) представляет собой функцию времени, а в качестве критерия оптимальности оценки используют некоторый функционал от погрешности оценки на временном интервале наблюдения, например средний квадрат погрешности.
В зависимости от вида используемых преобразований различают линейную и нелинейную фильтрацию, причем практическая реализация необходимых преобразовании может осуществляться как аппаратурным, так и программным способом.
Необходимо отметить, что для реализации оптимальной процедуры фильтрации необходима априорная информация о характеристиках изучаемого сигнала и помехи (случайной погрешности). Для более подробного изучения фильтрации следует обратиться к специальной литературе.
Рассмотрим основные методы уменьшения систематических погрешностей. Как известно, систематические погрешности делятся на постоянные и переменные. Наиболее распространенные методы исключения постоянных систематических погрешностей: введения поправок, замещения, компенсации погрешностей по знаку. Однако на практике, особенно при использовании информационно-измерительных систем для измерения неэлектрических величин в производственных условиях, доминирующую роль играют переменные систематические погрешности, вызванные изменениями температуры, влажности, давления окружающей среды, изменениями питающих напряжений, влиянием внешних электрических и магнитных полей и т. п. Следует отметить, что переменные систематические погрешности зависят от изменяющихся внешних воздействий, значения которых обычно не известны и поэтому проявляют себя как случайные функции времени. В это смысле от случайных погрешностей они отличаются тем, что представляют собой нестационарные случайные функции изменяющиеся во времени относительно медленно. Уменьшение подобных переменных систематических погрешностей представляет собой актуальную и достаточно сложную задачу.
Указанные выше методы исключения систематических погрешностей находят применение главным образом в лабораторной практике — их применение в автоматических измерительных устройствах и ИИС в производственных условиях и при изменениях систематических погрешностей в большинстве случаев невозможно. В связи с этим получили развитие методы уменьшения переменных систематических погрешностей, основанные на использовании структурной и (или) временной избыточности.
1). Конструктивно-технологические методы (экранирование, термостатирование, метод размещения элементов или узлов на растяжке, старение элементов, подбор контактных пар, теоретический расчет), 2). Поверка приборов. 3). Рандомизация или перевод систематических погрешностей в ряд случайных. 4). Метод инвертирования. 5). Метод замещения. 6). Использование отрицательной обратной связи (метод автокомпенсации). 7). Метод вспомогательных измерений. 8). Метод симметричных измерений. 9). Метод тестовых сигналов. 10). Метод образцовых сигналов. 11). Итерационный метод.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
