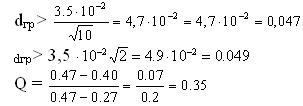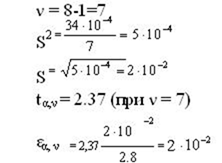Какими способами можно проверить правильность анализа

Специальные приемы проверки и повышения правильности

Помимо общего подхода к проверке правильности результатов анализа, основанного на их сравнении с независимыми данными при помощи статистических тестов, существует ряд специальных приемов, которые позволяют выявить, а во многих случаях и существенно снизить систематическую погрешность.

Одним из таких приемов служит способ варьирования размера пробы. В этом случае для анализа используют серию проб различного размера (например, несколько аликвот разного объема) и исследуют зависимость найденного содержания от размера пробы. Предположим, что методика анализа содержит систематическую погрешность , которая постоянна и не зависит от размера пробы. Погрешность такого типа называется аддитивной. Ее влияние состоит в том, что она увеличивает или уменьшает измеряемое значение аналитического сигнала на одну и ту же постоянную величину. Пусть истинное значение концентрации определяемого компонента составляет c₀. Тогда для аликвоты объемом V n₀=Vc₀. Измеренное значение количества определяемого компонента равно n_изм=n₀+ = Vc₀ + , а измеренное значение его концентрации — c_изм=n_изм/V = c₀ + /V. Таким образом, при наличии аддитивной систематической погрешности с увеличением объема аликвоты наблюдается закономерное изменение результата анализа — убывание либо возрастание в зависимости от знака .

Однако не всякая систематическая погрешность является аддитивной. Существуют погрешности другого типа, величина которых прямо пропорциональна размеру пробы (или содержанию определяемого компонента). Такие погрешности называются мультипликативными. Они увеличивают или (чаще) уменьшают значение аналитического сигнала в одно и то же число раз, т.е. изменяют наклон градуировочной зависимости. Очевидно, что такие систематические погрешности описанный способ выявить не может: в этом случае /V есть величина постоянная, и никакой зависимости c_изм от V не наблюдается. В то же время мультипликативные систематические погрешности можно значительно уменьшить с помощью специального способа градуировки, называемого способом добавок.

Основная цель способа добавок — обеспечение максимально точного соответствия условий градуировки и собственно определения (с. 4). При использовании способа добавок эти две операции совмещаются воедино: известные содержания определяемого компонента вводят как добавки непосредственно в анализируемый раствор и представляют градуировочную функцию в виде графика зависимости аналитического сигнала y от концентрации добавки c (рис. 4). Содержание компонента в анализируемом растворе находят путем экстраполяции полученной зависимости на нулевое (или фоновое, если оно известно — с. 5, 28) значение аналитического сигнала. Легко видеть, что в этом случае даже при наличии мультипликативной погрешности (т.е. изменении тангенса угла наклона градуировочного графика) получается правильный результат (ср. кривые 1 и 2 рис. 4). В то же время аддитивную систематическую погрешность способ добавок устранить не может (кривая 3 рис. 4).

Рис. 4. Градуировка по способу добавок. 1 — систематическая погрешность отсутствует, 2 — наблюдается мультипликативная систематическая погрешность, 3- аддитивная систематическая погрешность

Очень важным приемом повышения правильности результатов анализа является релятивизация — проведение отдельных аналитических операций в как можно более идентичных и строго контролируемых условиях с тем, чтобы возможные систематические погрешности взаимно скомпенсировать. Так, если показания весов содержат систематическую погрешность, то следует на одних и тех же весах в течение как можно более короткого промежутка времени взвесить сначала стаканчик с навеской, затем пустой стаканчик и найти массу навески по разности. По той же причине для отбора аликвот ОС и анализируемого раствора следует пользоваться одной и той же мерной посудой. Целям релятивизации служит также контрольный опыт — проведение пробы, не содержащей определяемого компонента, через все стадии анализа. Например, в спектрофотометрии можно приготовить раствор контрольного опыта (содержащий все используемые реактивы в количествах, рекомендуемых согласно методике) и использовать его в качестве раствора сравнения при измерениях оптической плотности.

И, наконец, еще один прием повышения правильности — это рандомизация. Здесь, наоборот, необходимо варьировать условия анализа случайным образом в достаточно широких пределах. Например, если каждая пипетка содержит свою систематическую погрешность объема, то для выполнения серии параллельных анализов образца можно отобрать каждую аликвоту новой пипеткой. При этом погрешность объема, применительно к каждой отдельной пипетке являющаяся систематической, по отношению ко всему множеству пипеток становится случайной, а среднее значение объема оказывается ближе к истинному, чем полученное при использовании только одной пипетки (рис. 5). Таким образом, рандомизация — это способ превращения систематической погрешности в случайную. В особо сложных случаях, когда систематические погрешности невозможно скомпенсировать, а причины и природа их неизвестны, рандомизация часто оказывается наиболее эффективным, а иногда и единственно возможным способом повышения правильности.

Источник

Метрологические основы аналитической химии (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8

Важнейшие способы получения информации о действительном (или, по крайней мере, не содержащем систематической погрешности) значении содержания определяемого компонента в анализируемом образце состоят в следующем.

1. Данные независимого анализа. Образец анализируют повторно, используя другую методику анализа, о которой известно (из опыта практического применения), что она не содержит систематической погрешности. При этом важно, чтобы такая методика была действительно независима от проверяемой, т. е. чтобы она по возможности принадлежала к другому методу и не содержала общих операций пробоподготовки. Еще лучше, если такой сравнительный анализ проводят в другой лаборатории, особенно официально аккредитованной.

2. Способ «введено — найдено». В этом случае аналитик сам готовит для анализа образец с известным содержанием определяемого компонента. Полученный результат («найдено») сравнивают с заданным содержанием («введено»).

3. Использование стандартных образцов. В качестве объекта анализа выбирают подходящий СО, а данные о содержании определяемого компонента берут из паспорта СО.

После получения тем или иным способом независимых данных о содержании определяемого компонента их необходимо сравнить с результатами, полученными с помощью проверяемой методики. Эта задача тоже далеко не так проста и требует отдельного рассмотрения.

Сравнение результатов анализов. Значимое и незначимое различие случайных величин

Вспомним еще раз, что любой результат измерения (в том числе среднее значение) представляет собой, вообще говоря, случайную величину. Поэтому численное различие двух результатов может быть вызвано случайными причинами и вовсе не свидетельствовать о том, что эти результаты действительно разные. Так, если результаты титрования двух аликвот равны, к примеру, 9.22 и 9.26 мл, то из этого нельзя заключить, что они имеют разный состав, поскольку случайная погрешность измерения объемов титранта составляет несколько сотых миллилитра (см. пример 1 на с. 14).

Подобное различие случайных величин, которое (при некоторой доверительной вероятности) может быть обусловлено только случайными причинами, в математической статистике называется незначимым. Очевидно, что если две величины различаются незначимо, то их можно рассматривать как два приближенных значения одного и того же, общего результата измерения. Напротив, значимое, т. е. превышающее уровень случайных погрешностей, различие свидетельствует о том, что соответствующие величины представляют собой два действительно разных результата. Естественно, различие можно считать значимым только тогда, когда оно достаточно велико. Граница, отделяющая значимые различия от незначимых, называется критической величиной. Ее можно рассчитать с помощью методов теории вероятностей.

Таким образом, задача сравнения результатов химического анализа состоит в том, чтобы выяснить, является ли различие между ними значимым. Сравнивать данные химического состава (и, шире, — любые экспериментальные данные) по обычным арифметическим правилам недопустимо! Вместо этого следует применять специальные приемы, называемые статистическими тестами или критериями проверки статистических гипотез. С некоторыми простейшими и в то же время наиболее важными для химика-аналитика статистическими тестами мы сейчас познакомимся.

Сравнение среднего и константы: простой тест Стьюдента

Вернемся к задаче проверки правильности результата химического анализа путем сравнения его с независимыми данными. Проверяемый результат, являясь средним из нескольких параллельных определений, представляет собой случайную величину . Результат же, используемый для сравнения, в ряде случаев можно считать точной (действительной) величиной a, т. е. константой. Это может быть тогда, когда случайная погрешность результата, используемого для сравнения, намного меньше, чем проверяемого, т. е. пренебрежимо мала. Например, в способе «введено-найдено» введенное содержание определяемого компонента обычно известно значительно точнее, чем найденное. Аналогично, при использовании СО паспортное значение содержания также можно считать точной величиной. Наконец, и при анализе образца независимым методом содержание компонента может быть определено с точностью, намного превышающей точность проверяемой методики, например, при проверке атомно-эмиссионной методики с помощью гравиметрической (о типичных величинах случайной погрешности различных методов см. с. 9). Во всех этих случаях задача сравнения данных с математической точки зрения сводится к проверке значимости отличия случайной величины от константы a.

Для решения этой задачи можно использовать уже известный нам подход, описанный выше (с. 13) и основанный на интервальной оценке неопределенности величины . Доверительный интервал для среднего, рассчитанный по формуле Стьюдента (16), характеризует неопределенность значения , обусловленную его случайной погрешностью. Поэтому если величина a входит в этот доверительный интервал, утверждать, что различие между и a значимо, нет оснований. Если же величина a в этот интервал не входит, различие между и a следует считать значимым. Таким образом, полуширина доверительного интервала, равная , является критической величиной для разности : различие является значимым, если

>. (17)

Для проверки значимости различия между средним и константой вместо вычисления доверительного интервала можно поступить следующим образом. Легко видеть, что выражение (17) эквивалентно выражению

. (18)

Величина, стоящая в левой части выражения (18), характеризует степень различия между и a с учетом случайной погрешности s(x). Она называется тестовой статистикой (и в общем случае обозначается в дальнейшем как x) для сравниваемых значений. Коэффициент Стьюдента, стоящий в правой части выражения (18), в этом случае непосредственно является критической величиной. Поэтому для проверки значимости различия между и a можно вычислить соответствующую тестовую статистику и сравнить ее с критическим значением, в данном случае табличным значением коэффициента Стьюдента. Если тестовая статистика превосходит критическое значение, различие между сравниваемыми величинами следует признать значимым.

Описанный способ сравнения случайных величин — вычисление тестовой статистики и сравнение ее с табличным критическим значением — является весьма общим. На таком принципе основано множество статистических тестов (или критериев) — процедур, призванных установить значимость различия между теми или иными случайными величинами. Тест, представленный формулой (18) и предназначенный для сравнения среднего значения и константы, называется простым тестом Стьюдента. В химическом анализе его следует применять всегда, когда возникает задача сравнения результатов анализа с каким-либо значением, которое можно считать точной величиной.

Пример 2. При определении никеля в стандартном образце сплава получена серия значений (% масс.) 12.11, 12.44, 12.32, 12.28, 12.42. Содержание никеля согласно паспорту образца — 12.38%. Содержит ли использованная методика систематическую погрешность?

Решение. Паспортное содержание никеля считаем действительным (точным) значением и применяем простой тест Стьюдента. Имеем:

s(x)=0.132, n=5, f=4, a=12.38.

Источник

Лекция 2. Правильность и статистическая обработка результатов анализа

Правильность и статистическая обработка результатов анализа

Статобработка результатов анализа

1. Задача количественного химического анализа найти содержание отдельных элементов в анализируемом материале. Главное требование к анализу — полученные результаты должны отражать истинное содержание элементов в пробе. Любое аналитическое определение состоит из следующих этапов:

статобработка результатов анализа.

Проба материала, поступающая в лабораторию должна быть представительной, т.е. состав пробы и всей партии обьекта анализа должны быть идентичными.

2. Необходимым этапом физико-химических методов является оценка возпроизводимости и правильности анализа. Погрешности бывают грубыми, систематическими и случайными.

Грубые ошибки: а) ошибка аналитика (неправильный отбор аликвоты), б) выход из строя измерительных приборов.

Систематические ошибки — это односторонние погрешности, вызванные неисправностью измерительного прибора, недостатком метода.

Случайные ошибки не имеют видимой причины. Оценка случайных погрешностей проводится на основе теории математической статистики. Для характеристики качества анализа рекомендуется использовать определяемые понятия правильность и воспроизводимость, под которыми надо понимать термин точность. Воспроизводимость представляет собой необходимый, но недостаточный признак правильности результатов. Без удовлетворительной возпроизводимости нет и точности. Однако даже хорошая воспроизводимость вовсе не доказывает точность метода.

Правильность анализа (ПА) характеризуется расхождением между средним и истинным результатом. ПА нельзя установить посредством статистской обработки результатов. Надо применять другие, экспериментальные методы проверки правильности. К ним относят следующие методы:

А) Проведение анализа двумя или несколькими независимыми методами. Применение стандартных образцов (СО). СО- это эталоны химического состава материалов. Каждый СО снабжен официальным документом — паспортом, в которой указано аттестованное содержание отдельных элементов. Чтобы установить правильность анализа какого-либо материала, из имеющегося в лаборатории набора СО выбирают тот, который по своему составу в наибольшей степени приближается к предполагаемому составу анализируемой пробы. Затем проводят параллельный анализ пробы и стандартного образца, устанавливая содержание отдельных элементов в них. Считается, что использованный метод анализа дает правильные результаты, если найденное содержание отдельных элементов в стандартном образце соответствует паспортным данным, установленным при аттестации этого образца.

B) Метод добавок. Ведут несколько параллельных определений, прибавляя к некоторым пробам точно известные количества определяемого элемента. При правильном анализе количество элемента, найденное в пробах с добавками и без них, должно соответствовать количеству добавки. Например, определяя железо в растворе нашли, что проба без добавки содержала 0,2378 г Ғе203, а проба с добавкой 0,1000 г Ғе2О3 — 0,3375 г Ғе2Оэ. Разность 0,0997г = 0,1000 г.. Разность 0,0997г = 0,1000 г. Анализ можно считать правильным.

При полном анализе, какого либо материала сумма всех компонентов должна быть равной 100% или незначительно отличаться от этого значения.

Применяя эти методы, можно говорить о правильности анализа. Тем не менее, систематические погрешности все же возможны. Важно, чтобы они не выходили за некоторые пределы.

Рассмотрим зависимость результатов определения от наличия систематических погрешностей.

В одних случаях результат может отличаться от истинного всегда на одно и тоже значение, т. е. погрешность будет постоянной независимо от размера навески.

В других случаях систематическая погрешность влияет на результаты анализа иначе. Увеличение навески анализируемого материала влечет за собой возрастание только абсолютной погрешности, однако относительная погрешность остается при этом одной и той же. Пример: иодометрическое определение меди в сплавах с примесями железа.

2Сu2+ + 4I- =2СuI + I2

Затем I2 +2 Nа2S203 = 2NаI + Nа2S406 и по расходу тиосульфата вычисляют соединение Си 2+ . Однако Ғе3+ с иодид-ионами I- дают I2:

2 Ғе3+ +2I- = 2Ғе2++I2

Поэтому в присутствии Ғе3+получаются повышенные результаты для Си2+, причем абсолютная погрешность возрастает с увеличением размера навески. Однако относительная погрешность не зависит от количества взятого для анализа материала. Предположим, что навеске 0,1г отвечает + погрешность 0,2 мг, тогда при навеске 0,2 г, она увеличивается до 0,4мг, однако в обоих случаях относительная погрешность остается неизменной и составит:

3. Статистическая обработка (СТО) результатов анализа имеет две основные задачи:

представить результаты многих определений в компактной форме.

оценить надежность полученных результатов, т.е. степень их соответствия истинному определяемого элемента в образце.

Среднее значение полученного результата по разным причинам может отличаться от истинного. Разница между ними определяет правильность определения и представляет собой систематическую погрешность, которая повторяется от опыта к опыту. Причиной случайной погрешности могут быть несовершенство приборов , влияние посторонних компонентов, загрязнение реактивов и т.д. Например, при фотометрическом определении Си2+ получены десять значений оптической плотности D:

Математическая обработка результатов анализа

Полученные расхождения можно объяснить случайными погрешностями. Однако, если в результате неправильно нанесенной шкалы ФЭК постоянно получают завышенные показатели D, это будет причиной систематической ошибки, повторяющейся от опыта к опыту.

Рассмотрим обработку данных. Сначала выводим среднее арифметическое

Х = 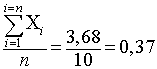(2.1)

Отклонения dі характеризуют погрешность определения. По значениям di вычисляем дисперсию S2.

(2.2)

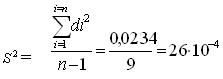
S = называют стандартным отклонением: (2.3)

S =

Известна еще одна величина – точность прямого измерения (ε), которую определяют по известному уравнению. При использовании этого уравнения задаются значением надежности (α), т.е. долей случаев в которых при данном числе измерений среднем арифметическом лежит в определенных пределах. При физико-химических измерениях обычно принимают α = 0,95 или α = 0,99 . Это означает, что 95 или 99% всех измерений лежит в указанных пределах:

(2.4)

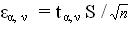
Коэффициент t α,ν называют критерием Стъюдента. ν = n-1 и его называют числом степеней свободы.Величину t α,ν находят по специальным таблицам в зависимости от α и ν = n — 1. Их значения приведены в таблице 2.

Коэффиценты Стьюдента t α,ν

Исходя из таблицы № 1:

ν = 10-1= 9; = 10 = 3,2

Это большая погрешность в таблице 1 разброс составляет от 0,27 до 0,47. Видимо здесь имеют место какие-то грубые погрешности. Такие грубые погрешности можно определить при помощи трех критериев:

по стандартному отклонению d груб >3S/ (2.5)

по точности прямого измерения (2.6)

по Q — критерию, которую вычисляют по формуле: 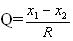(2.7)

R — размах варьирования (разность между предельными значениями измеряемой величины) Значения Q-критерия приведены в таблице 3.

Таблица 2.3 Значения Q-критерия

Применяя эти три критерия, получаем:

По первым двум критериям первое и десятое измерения должны быть исключены как грубые погрешности.

А по Q — критерию необходимость исключения ставится под сомнение, так как значение Q меньше табличного. Поэтому рекомендуют проверить такие значения по одному из первых критериев.

Теперь делаем вторичную обработку (исходя из табл. 2, данные заносим в табл. 1)

Следовательно, D= 0.37 ұ 0.02 (Dср = 0.37)

После исключения грубых погрешностей точность измерений значительно повышается.

Т.о. стандартное отклонение S, а также точность прямого измерения S характеризуют точность результатов наблюдения

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник