Электронная библиотека
Для повышения точности измерений рекомендуется производить не одно, а несколько измерений одной и той же величины C при одних и тех же условиях. При многократных измерениях погрешность измерения от случайных ошибок уменьшается в раз, где n – число измерений.
На основе закона нормального распределения случайных величин можно многократным измерением одних и тех же величин одним и тем же измерительным средством уменьшить влияние случайных ошибок, так как они усредняются, и в итоге повышается точность результата измерения.
Это действие усреднения результатов многократных измерений подтверждается народной пословицей «семь раз отмерь – один раз отрежь». Пословица обращает внимание на то, что однократное «отмеривание» может быть неточным, а семикратное «отмеривание» предохраняет от промахов.
Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей.
Оценками рассеяния результатов в ряду измерений могут быть:
· средняя арифметическая погрешность (по модулю);
· средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение, экспериментальное среднее квадратическое отклонение);
· доверительные границы погрешности (доверительная граница или доверительная погрешность).
Размах – это оценка Rn рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле
где Хmax и Хmin – наибольшее и наименьшее значения физической величины в данном ряду измерений.
Рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностный характер.
Проведя несколько повторных измерений одной и той же величины и получив различные результаты Xi, определяют среднее арифметическое значение ряда измерений и принимают его за истинное значение измеряемой величины Cист, т.е. принимают Cист = :
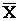
где n – число единичных измерений в ряду.
Средняя квадратическая погрешность результатов единичных измерений в ряду измерений – это оценка S рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около их среднего значения, вычисляемая по формуле
где Хi – результат i—го единичного измерения; `Х — среднее арифметическое значение измеряемой величины из n единичных результатов.
На практике широко распространен термин среднее квадратическое отклонение – (СКО). С точки зрения упорядочения совокупности терминов, родовым среди которых является термин «погрешность измерения», целесообразно применять термин «средняя квадратическая погрешность» (СКП). При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов единичных измерений.
Ценность результата многократных измерений значительно повышается, если кроме среднего арифметического значения будет определена средняя квадратическая погрешность среднего арифметического в виде S`Х, которая зависит от значения S и количества проведения измерений n:
При ответственных измерениях проводят ряд повторных измерений и на основе полученных результатов всех измерений подсчитывают среднее арифметическое значение и среднюю квадратическую погрешность S, а потом и погрешность среднего арифметического S`Х.
Доверительные границы погрешности результата измерений – это наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.
Доверительные границы распределения вычисляются как ± t S, ± t S`Х, где S, S`Х – средние квадратические погрешности соответственно единичного и среднего арифметического результатов измерений; t – коэффициент, зависящий от доверительной вероятности Р и числа измерений n.
t = 2 при Р = 94,5 %;
t = 3 при Р = 99,73 %.
Для нормального закона распределения случайных величин используется t = 3.
Таким образом, результат измерения или истинное значение измеряемой величины Xист представляется так:
Полученный результат измерения не является одним конкретным числом, а представляет собой интервал, внутри которого с некоторой вероятностью Р находится истинное значение измеряемой величины.
Пример. Для определения размера отверстия опытной детали измерили его нутромером повышенной точности 10 раз (n = 10).
При подсчете получили = 60,012 мм и S = 0,00115 мм. Истинное значение размера отверстия детали представится так:
Xист = 60,012 ± = 60,012 ± 0,0011 мм.
Результат расчета показывает, что истинное значение размера отверстия опытной детали определено с точностью ± 1,1 мкм и с вероятностью 0,9973, т.е. только в 0,27 % случаев может оказаться, что погрешность будет не 1,1 мкм.
В случае многократных повторных измерений одной и той же величины одним и тем же методом измерения и при отсутствии систематических погрешностей за предельную погрешность измерения в ряду измерений, обозначаемую Dпр, принимается значение, равное ± 3 S. Так, если бы целью десятикратных измерений являлось определение предельной погрешности данного метода измерения, то эта погрешность для любого отдельного измерения будет равна: Dпр = ± 3 S = ± 3 × 0,0011 = ± 0,003 мм.
Если при многократных измерениях появится погрешность больше 3 S, то такую погрешность считают грубой, и результат измерения с такой погрешностью отбрасывают.
Задания к разделу 8: Ответить на вопросы по своему варианту (номер варианта соответствует последней цифре номера зачетной книжки).
1. Что такое погрешность результата измерения?
2. Какие погрешности называются случайными?
1. Что такое погрешность средства измерения?
2. Что такое промах? Причины возникновения промахов.
1. Что такое истинное значение физической величины?
2. Как отразится на результате измерений следование русской поговорке: «Семь раз отмерь – один раз отрежь»?
1. Что такое действительное значение физической величины?
2. Что является оценками рассеяния результатов в ряду измерений?
1. Что такое результат измерения?
2. Что такое размах и как он определяется?
1. Какая погрешность называется систематической?
2. Что такое средняя квадратическая погрешность результатов единичных измерений в ряду измерений и как она определяется?
1. Приведите классификацию систематических погрешностей.
2. Что такое средняя квадратическая погрешность среднего арифметического и как она определяется?
1. Какая погрешность называется постоянной?
2. Что такое доверительные границы погрешности результата измерения?
1. Какие погрешности называются прогрессивными?
2. Как вычисляются доверительные границы распределения?
1. Какие погрешности называются периодическими?
2. Как определяется истинное значение измеряемой величины?
Источник
Методы и способы повышения точности измерений. Часть первая
ведущий специалист — начальник группы метрологической экспертизы отдела главного метролога ФГУП «ОКБ «Факел», г. Калининград
Ужесточение требований к качеству продукции во многих случаях проявляется в виде ужесточения требований к допускам на контролируемые параметры сырья и продукции, а, следовательно, и в виде ужесточения (повышения) требований к точности измерений параметров и характеристик сырья и продукции. В связи с этим сотрудники метрологических служб промышленных предприятий должны достаточно уверенно разбираться в современных методах и способах повышения точности измерений.
Читатели журнала «Главный метролог» неоднократно высказывали пожелания о публикации материалов, посвященных вопросам повышения точности измерений. С учетом этих пожеланий редакция приняла решение о публикации в рубрике «В ПОМОЩЬ НАЧИНАЮЩИМ МЕТРОЛОГАМ» цикла статей, посвященных тому важному разделу прикладной метрологии, о котором идет речь. Над подготовкой этого цикла статей любезно согласилась поработать Ольга Владимировна Полякова, «серебряный» призер Первой Всероссийской метрологической олимпиады, ведущий специалист — начальник группы метрологической экспертизы отдела главного метролога широко известного в стране предприятия — ФГУП «ОКБ «Факел» (г. Калининград). О.В.Полякова уже знакома читателям нашего журнала по циклу её статей, посвященных метрологической экспертизе технической документации и публиковавшихся ранее в рубрике «В помощь начинающим метрологам». Ниже вниманию читателей предлагается первая часть задуманного материала
Одна из главных задач метрологических служб предприятий — обеспечение требуемой точности измерений, выполняемых на различных стадиях производства продукции. В условиях острой конкурентной борьбы за первенство на российском и международном рынках возрастают требования, предъявляемые к качеству выпускаемых изделий, и появляется очередная задача — повышение точности измерений.
Повышение точности измерений всегда способствовало развитию не только отдельной отрасли народного хозяйства, но и мирового научно-технического прогресса, улучшению жизни и здоровья людей. Достаточно вспомнить, что значительное повышение точности измерений неоднократно являлось основной предпосылкой фундаментальных научных открытий.
Так, повышение точности измерения плотности воды в 1932 году привело к открытию тяжелого изотопа водорода — дейтерия, определившего бурное развитие атомной энергетики.
Благодаря гениальному осмыслению результатов экспериментальных исследований по интерференции света, выполненных с высокой точностью и опровергнувших существовавшее до того мнение о взаимном движении источника и приемника света, Альберт Эйнштейн создал свою всемирно известную теорию относительности.
Основные методы повышения точности измерений, применяемые сегодня на практике, изложены в рекомендациях по межгосударственной стандартизации РМГ 64-2003 «ГСИ. Обеспечение эффективности при управлении технологическими процессами. Методы и способы повышения точности измерений».
Данные рекомендации являются моей настольной книгой, думаю, что и для большинства моих коллег тоже. Тех, кто знаком с этим документом, возможно, так же, как и меня, мог заинтересовать вопрос: в чём заключается разница между методом и способом повышения точности измерений?
Метрология, как известно, наука точная и требует однозначного понимания. В названии РМГ 64-2003 между указанными словами стоит союз «и», а в тексте встречается союз «или». Эти союзы могут соединять как два похожих по значению понятия, так и отличающихся.
За разъяснением значений слов «метод» и «способ» я обратилась сразу к нескольким словарям и нашла в них следующие определения:
Метод (от греческого methodos) — способ достижения какой-либо цели, решения конкретной задачи; совокупность приемов или операций практического или теоретического освоения (познания) действительности (Большой энциклопедический словарь).
Метод — способ теоретического исследования или практического осуществления чего-нибудь (словарь С.И.Ожегова)
Способ — действие или система действий, применяемые при исполнении какой-нибудь работы, при исполнении чего-нибудь (словарь С.И.Ожегова)
Способ — тот или иной порядок, образ действий, метод в исполнении какой-нибудь работы, в достижении какой-нибудь цели (словарь Д.Н.Ушакова)
После сравнения данных определений вывод становится очевиден — слова «метод» и «способ» являются синонимами и имеют одно и то же значение, следовательно, для нас, метрологов, не важно, как мы назовем применяемые нами действия по повышению точности измерений — способом или методом, важна их суть.
Затрагивая эту актуальную тему, я хочу осветить те вопросы, которые, на мой взгляд, помогут начинающим метрологам научиться последовательно и правильно решать задачи по повышению точности измерений.
Прежде чем рассматривать конкретные методы или способы повышения точности измерений, следует вспомнить:
Источник
Наиболее часто применяемые на практике методы и способы повышения точности измерений
«На практике наиболее часто применяются следующие методы и способы повысить точность измерений:
1) Замена менее точного средства измерений на более точное.
При отсутствии более точного средства измерений его можно разработать.
Данный способ повышения точности измерений используется, когда преобладает инструментальная составляющая погрешности измерений.
Для измерительных каналов на более точные заменяют только те средства измерений, погрешности которых преобладают при расчете суммарной погрешности канала.
2) Выбор верхнего предела измерений средств измерений, для которых нормированы приведенные основная и дополнительная погрешности, таким, чтобы ожидаемые значения измеряемой величины находились в последней трети предела измерений.
Таким способом можно уменьшить относительную погрешность средств измерений.
3) Ограничение условий применения средств измерений.
Этим способом пользуются в случае доминирования дополнительных погрешностей средств измерений, которые возникают, например, при значительных отклонениях от
нормальных значений температуры окружающего воздуха; при влиянии электромагнитных полей, вибрации и т.д.
В этих случаях уменьшают подобные влияния путем установки кондиционеров, защитных экранов от электромагнитного воздействия, амортизаторов для снижения вибрации.
4) Индивидуальная градуировка средства измерений.
Данный способ повышения точности измерений применяется в случае преобладания систематических составляющих погрешности средств измерений. Систематические составляющие погрешности средств измерений (например, для термометров сопротивления и термопар) можно значительно уменьшить путем внесения в результаты измерений поправок, полученных при индивидуальной градуировке.
5) Использование метода замещения.
С помощью такого метода исключают систематические погрешности. Он заключается в том, что после измерения измеряемая величина заменяется переменной образцовой мерой, значение которой подбирается таким образом, чтобы в измерительной схеме получить одинаковое показание прибора. При этом значение измеряемой величины принимается равным значению образцовой меры.
Пример: измерение электрического сопротивления на мосте постоянного тока.
6) Внедрение способов контроля работоспособного состояния средств измерений в процессе их эксплуатации.
Это мероприятие способствует выявлению, исключению или снижению метрологических отказов в средствах измерений. Во многих случаях системы контроля работоспособности средств измерений в процессе эксплуатации эффективны без каких-либо ограничений на составляющие погрешности средств измерений и их случайный или систематический характер.
7) Автоматизация измерительных процедур.
Такое мероприятие снижает трудоемкость измерений, способствует исключению субъективных погрешностей, возникающих при обработке диаграмм, вычислении промежуточных и конечных результатов измерений, приготовлении проб для анализов и других операций, выполняемых человеком.
8) Использование метода обратного преобразования.
Метод используется для автоматической коррекции погрешности средств измерений.
Подбирается такой обратный преобразователь, статическая реальная функция преобразования которого должна совпадать с функцией, обратной номинальной характеристике преобразования средства измерений.
Обратный преобразователь должен быть значительно точнее прямого преобразователя.
На вход обратного преобразователя подается реальный выходной сигнал средства измерений. Разность двух сигналов – входной сигнал средства измерений минус выходной сигнал обратного преобразователя — соответствует погрешности средства измерений и может использоваться для выработки корректирующего сигнала в системе настройки и в системе введения поправок.
При этом методе корректируются инструментальные погрешности любого происхождения, т.к. точность коррекции определяется высокой точностью обратного преобразователя. Коррекция осуществляется в течение всего режима измерения.
Метод широко используется при измерении, например, электрических величин.
9) Выполнение многократных наблюдений с последующим усреднением их результатов.
Этот метод применяется при преобладании случайной составляющей погрешности измерений. Как известно, случайная составляющая погрешности измерений среднего значения меньше случайной составляющей погрешности измерений текущих значений.
Метод используется тогда, когда в течение интервала времени усреднения не происходит заметное изменение текущих значений измеряемой величины, но погрешность измерений текущих значений в течение этого же интервала существенно меняется.
10) Использование тестовых сигналов.
Этот метод повышения точности измерений применяется в измерительных системах для измерений электрических и неэлектрических величин.
Суть метода состоит в определении параметров статической функции преобразования (СФП) с помощью дополнительных преобразований тестов, каждый из которых функционально связан с измеряемой величиной. Тестовые методы позволяют повышать точность измерений за счет уменьшения систематических и так называемых квазисистематических погрешностей.
11) Использование информационной избыточности.
Информационная избыточность – такое состояние измерительной информации, при котором она больше необходимой для реализации функций управления объектом.
Пример использования информационной избыточности для повышения точности измерений — включение в измерительную систему дополнительных средств измерений, измеряющих одну и ту же величину, и усреднение их показаний.
Другой пример — наличие связей между измеряемыми величинами, обусловленных свойствами объекта измерений или управления. Эти связи могут быть использованы для исключения промахов при измерении отдельных величин и для повышения точности измерений всей совокупности измеряемых величин.
12) Разработка или совершенствование методик выполнения измерений
Если доминируют методические составляющие погрешности измерений, то этот способ повышения точности измерений является единственно эффективным.
В ИИС и АСУ ТП составляющие методической погрешности измерений, обусловленные отличием алгоритма вычислений от функции, строго определяющей зависимость результатов вычислений от аргументов измеряемых прямым методом величин, уменьшают применением более совершенного алгоритма.
При существенной методической погрешности измерений средних или интегральных значений, обусловленной ограниченным числом «точек» измерений или отклонениями действительных значений от номинальных значений неизмеряемых величин, входящих в функцию в виде констант, соответствующее совершенствование методики выполнения измерений дает заметный эффект в повышении точности измерений. Методики выполнения измерений могут быть усовершенствованы изменением алгоритма обработки результатов измерений. В этом случае проводят аттестацию алгоритма в соответствии с нормативными документами.
Источник





