Какими способами можно определить равносильность формул логики

Равносильные формулы алгебры высказываний

Равносильные формулы алгебры высказываний

1. Услуги проектирования
2. Алгебра логики [Г.И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв]
3. Равносильные формулы алгебры высказываний

Равносильные формулы алгебры высказываний

Две формулы алгебры высказываний $A$ и $B$ называются равносильными или эквивалентными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы элементарных высказываний.

Равносильность формул будем обозначать знаком $\equiv$, а запись $A\equiv B$ означает, что формулы $A$ и $B$ равносильны.

Например, равносильны формулы:

Тождественно истинная формула

Формула $A$ называется тождественно истинной < или тавтологией >, если она принимает значение 1 при всех значениях входящих в нее переменных.

Например, тожественно истинны формулы $X\vee \overline < X >$, $X\rightarrow (Y\rightarrow X)$

Тождественно ложная формула

Формула $A$ называется тождественно ложной < или противоречием >, если она принимает значение 0 при всех значениях входящих в нее высказываний.

Например, тождественно ложна формула $X\wedge \overline < X >$

Выполнимая формула

Формула $A$ называется выполнимой, если она принимает значение 1 при всех значениях входящих в нее высказываний.

Например, выполнима формула $X\vee \overline < X >$

Ясно, что отношение равносильности рефлексивно, симметрично и транзитивно.

Группы равносильностей

Между понятиями равносильности и операцией $\leftrightarrow$ существует следующая связь: если формулы $A$ и $B$ равносильны, то формула $A\leftrightarrow B$ — тавтология, и обратно, если формула $A\leftrightarrow B$ — тавтология, то формулы $A$ и $B$ равносильны.

Важнейшие равносильности алгебры высказываний можно разбить на следующие группы.

Равносильности алгебры Буля

Закон двойного отрицания: $\overline < \overline < X >> \equiv X$

Коммутативность: $X\wedge Y\equiv Y\wedge X$; $X\vee Y\equiv Y\vee X$

Ассоциативность: $X\wedge (Y\wedge Z)\equiv (X\wedge Y)\wedge Z$; $X\vee (Y\vee Z)\equiv (X\vee Y)\vee Z$

Дистрибутивность $\wedge$ относительно $\vee$: $X\wedge (Y\vee Z)\equiv (X\wedge Y)\vee (X\wedge Z)$; $(X\vee Y)\wedge Z\equiv (X\wedge Z)\vee (Y\wedge Z)$

Дистрибутивность $\vee $ относительно $\wedge $: $X\vee (Y\wedge Z)\equiv (X\vee Y)\wedge (X\vee Z)$; $(X\wedge Y)\vee Z\equiv (X\vee Z)\wedge (Y\vee Z)$

Законы де Моргана: $\overline < X\wedge Y >\equiv \overline < X >\vee \overline < Y >$; $\overline < X\vee Y >\equiv \overline < X >\wedge \overline < Y >$

Законы поглощения: $X\wedge (Y\vee X)\equiv X$; $X\vee (Y\wedge X)\equiv X$

Законы идемпотентности: $X\wedge X\equiv X$; $X\vee X\equiv X$

Свойства констант: $X\wedge 1\equiv X$; $X\vee 1\equiv 1$; $X\wedge 0\equiv 0$; $X\vee 0\equiv X$

Закон противоречия: $X\wedge \overline < X >\equiv 0$

Закон исключения третьего: $X\vee \overline < X >\equiv 1$

Равносильности, выражающие одни логические операции через другие

$X\leftrightarrow Y\equiv (X\rightarrow Y)\wedge (Y\rightarrow X)$

$X\leftrightarrow Y\equiv (\overline < X >\vee Y)\wedge (\overline < Y >\vee X)$

$X\leftrightarrow Y\equiv (X\wedge Y)\wedge (\overline < Y >\wedge \overline < X >)$

$X\rightarrow Y\equiv \overline < X >\vee Y$

$X\wedge Y\equiv \overline < \overline < X >\vee \overline < Y >> $

$X\vee Y\equiv \overline < \overline < X >\wedge \overline < Y >> $

$X | Y\equiv \overline < X\cdot Y >$

$X \downarrow Y\equiv \overline < X\vee Y >$

$X \rightarrow Y\equiv \overline < X >\vee Y$

$X \bigoplus Y\equiv (X \cdot \bar < Y >)\vee (\bar < X >\cdot Y)$

$X \sim Y\equiv \overline < X \bigoplus Y >\equiv (XY)\vee (\bar < X >\bar < Y >)$

Далее:

Теорема об алгоритме распознавания полноты

Поверхностный интеграл первого рода и его свойства

Лемма о построении множества $[F]_$

Свойства тройного интеграла

Несобственные интегралы от неограниченной функции

Упрощение логических функций

Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы

Определение тройного интеграла. Теорема существования тройного интеграла

Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных

Нормальные формы

Теорема Остроградского

Полином Жегалкина. Пример.

Вычисление двойного интеграла. Двукратный интеграл

Вычисление криволинейного интеграла второго рода. Примеры.

Огравление $\Rightarrow $

Источник

MT1102: Линейная алгебра (введение в математику)

Определение

Формулы алгебры высказываний %%X%% и %%Y%% называют равносильными (эквивалентными, тождественными), если при любых значениях переменных, входящих в эти формулы, значение истинности формул %%X%% и %%Y%% совпадают.

Пример

Пусть даны формулы $$ X = A \rightarrow B, Y = \overline \rightarrow \overline . $$

Построим таблицу истинности для этих двух формул

%%A%%	%%B%%	%%X = A \rightarrow B%%	%%Y = \overline \rightarrow \overline%%
%%0%%	%%0%%	%%1%%	%%1%%
%%0%%	%%1%%	%%1%%	%%1%%
%%1%%	%%0%%	%%0%%	%%0%%
%%1%%	%%1%%	%%1%%	%%1%%

Как видно из таблицы, истинностные значения данных формул совпадают при любых значениях %%A%% и %%B%%, следовательно, эти две формулы равносильны. Равносильность формул %%X%% и %%Y%% записывается в виде %%X \equiv Y%%.

Теоремы о равносильности формул

Теорема. Справедливы следующие равенства формул.

1. Закон тождества $$ A \equiv A $$
2. Закон коммутативности $$ \beginA \land B \equiv B \land A \\ A \lor B \equiv B \lor A \end $$
3. Закон ассоциативности $$ \beginA \land (B \land C) \equiv (A \land B) \land C \\ A \lor (B \lor C) \equiv (A \lor B) \lor C \end $$
4. Закон идемпотентности $$ \beginA \land A \equiv A \\ A \lor A \equiv A \end $$
5. Закон дистрибутивности $$ \beginA \land (B \lor C) \equiv (A \land B) \lor (A \land C) \\ A \lor (B \land C) \equiv (A \lor B) \land (A \lor C) \end $$
6. Законы де Моргана $$ \begin\overline \equiv \overline \lor \overline \\ \overline \equiv \overline \land \overline \end $$
7. Закон двойного отрицания $$ \overline<\overline> \equiv A $$
8. Закон непротиворечия $$ A \land \overline \equiv 0 $$
9. Закон исключения третьего $$ A \lor \overline \equiv 1 $$
10. Тождества $$ \beginA \land 1 \equiv A,

A \land 0 \equiv 0 \\ A \lor 0 \equiv A,

Где %%1%% — тождественно истиннная формула, а %%0%% — тождественно ложная формула.

Теорема дается без доказательства, так как эти формулы легко проверить, используя таблицы истинности.

Теорема. Для произвольной формулы существует равносильная ей формула, которая содержит только знаки отрицания и дизъюнкции.

Действительно, в произвольной формуле %%X%% могут присутствовать знаки конъюнкции, импликации и эквиваленции. Избавимся от этих знаков, заменяя подформулы, содержащие эти знаки, на равносильные им по следующим правилам:

1. Заменяем %%A \leftrightarrow B%% на %%A \leftrightarrow B \equiv (A \rightarrow B) \land (B \rightarrow A)%%.
2. Заменяем %%A \rightarrow B%% на %%\overline \lor B%%.
3. Заменяем %%A \land B%% на %%\overline <\overline\lor \overline>%%.

Но использование только двух знаков очень неудобно, так как приводит к очень громоздким формулам, именно поэтому, обычно, используют три основных знака: отрицание, конъюнкция и дизъюнкция.

Обратная и противоположная теоремы

Пусть %%T%% некоторая теорема, имеющая вид $$ A \rightarrow B. $$

Назовем теорему %%T = A \rightarrow B%% прямой теоремой. Составим следующие высказывания:

Между этими теоремами есть следующие связи:

Источник

Какими способами можно определить равносильность формул логики

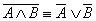
Законы де Моргана

Операции с константами

Приведенные выше законы, во-первых, можно рассматривать как свойства операций отрицания, дизъюнкции и конъюнкции. А, во-вторых, эти законы служат для упрощения сложных логических формул. Так, коммутативный закон позволяет переставлять выражения, связанные операциями дизъюнкции Ú и конъюнкции Ù , и выполнять их в любой последовательности (Вспомним из элементарной математики: «От перемены мест слагаемых сумма не меняется»):

B Ú Ú ( С Ú B ) º ( С Ú B ) Ú B Ú º B Ú ( С Ú B ) Ú .

Согласно ассоциативному закону можно опускать скобки между любым числом членов, связанных одинаковыми операциями Ú или Ù :

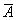
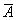
( B Ú ) Ú ( С Ú B ) º B Ú Ú С Ú B .

Законы идемпотентности дают возможность одинаковые выражения, связанные конъюнкцией или дизъюнкцией, заменять одним:

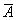
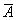
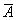
B Ú Ú С Ú B º B Ú B Ú Ú С º B Ú Ú С.

С помощью дистрибутивных законов можно раскрывать скобки при выполнении операций Ú или Ù . Дистрибутивность конъюнкции относительно дизъюнкции в логике аналогична соответствующему закону алгебры: a × ( b + c ) = a × b + a × c . Для дизъюнкции подобную аналогию провести нельзя.

Из рассмотренных тождеств можно заметить, что знаки Ú и Ù симметричны. Каждому тождеству со знаком Ú соответствует аналогичное со знаком Ù .

Рассмотрим формулы, в которых содержатся лишь операции отрицания, дизъюнкции и конъюнкции. Как было показано выше, любую формулу можно привести к такому виду. Для таких формул можно сформулировать так называемый закон двойственности.

Закон двойственности. Если в двух равносильных формулах заменить дизъюнкцию конъюнкцией, единицу нулем и наоборот, то полученные формулы будут также равносильны.

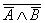
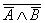
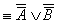
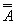
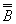
Из законов Моргана вытекает еще одно важное свойство. Оказывается, что операцию дизъюнкция можно выразить через отрицание и конъюнкцию, и наоборот. Действительно, рассмотрим формулу . На основании закона Моргана получим: . А знаки двойного отрицания можно убрать º А и º В. Следовательно,

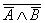
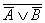
А Ú В º . Аналогично доказывается равносильность А Ù В º , выражающая конъюнкцию через отрицание и дизъюнкцию.

Таким образом, для любой логической формулы можно найти равносильную, содержащую только две логические операции: дизъюнкцию и отрицание или конъюнкцию и отрицание. При этом, естественно, формулы становятся более длинными и менее обозримыми.

Подобно этому, в элементарной алгебре степень с целочисленным показателем можно выразить через произведение одинаковых множителей: 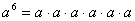, а произведение, в свою очередь, заменить сложением 5 × a = a + a + a + a + a . Ясно, что избыточность в определениях и обозначениях не всегда является недостатком.

отнюдь не ограничивается краткостью записи логических формул. Эти операции эффективно используются при описании закономерностей логических заключений.

Основы логики высказываний в какой-то мере аналогичны обычной элементарной алгебре, хотя и имеют свои характерные закономерности. Поэтому эта часть логики еще называется булевой алгеброй в честь английского математика Джорджа Буля (1815 – 1864). Логическое исчисление Буля было изложено в его работах «Математический анализ логики, или Опыт исчисления дедуктивных умозаключений» ( 1847 г .), «Логическое мышление» (1848г.), «Исследование законов мышления, на коих основаны математические теории логики и вероятностей» (1854г.). Идеи Дж. Буля были развиты Огастесом де Морганом, Чарльзом Пирсом и др.

Источник

Какими способами можно определить равносильность формул логики

Равносильные формулы алгебры логики

Определение. Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).

Обозначение. A ≡ B .

.

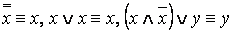
Определение. Формула A называется тождественно истинной (тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных (напр., ).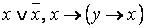

Определение. Формула A называется тождественно ложной (противоречием), если она принимает значение 0 при всех значениях входящих в нее переменных (напр., ).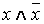

Утверждение. Отношение равносильности рефлексивно, симметрично, транзитивно.

Связь между понятиями равносильности и эквивалентности: если формулы A и B равносильны, то формула A ↔ B тавтология, и обратно, если формула A ↔ B тавтология, то формулы A и B равносильны.

Равносильности алгебры логики можно разбить на 3 группы:

1. Основные равносильности.

· – законы идемпотентности;

· ;

· ;

· ;

· ;

· – закон противоречия;

· – закон исключенного третьего;

· – закон снятия двойного отрицания;

· – законы поглощения.

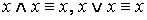
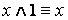
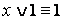
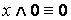
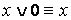
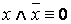
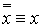
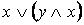
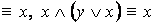
1. Равносильности, выражающие одни логические операции через другие:

· ;

· ;

· ;

· ;

· ;

· .

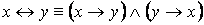
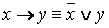
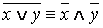
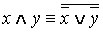
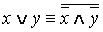
Замечание. Из равносильностей группы 2 следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание, или дизъюнкцию и отрицание. Дальнейшее исключение операций невозможно. Например, если использовать только конъюнкцию, то уже такая простая формула, как 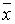не может быть выражена с помощью операции конъюнкции.

Существуют операции, с помощью которых может быть выражена любая из 5 логических операций:

1) Связка Шеффера – дизъюнкция отрицаний.

Обозначение. x | y ≡ (« x не совместно с y »).

Логические значения связки Шеффера описываются следующей таблицей истинности:

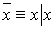
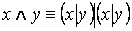
Имеют место следующие равносильности: а) ; б) .

2) Связка Лукасевича – конъюнкция отрицаний.

Обозначение . x ↓ y ≡ 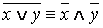(«ни x , ни y »).

Логические значения связки Лукасевича описываются следующей таблицей истинности:

2. Равносильности, выражающие основные законы алгебры логики:

· – коммутативность конъюнкции;

· – коммутативность дизъюнкции;

· – ассоциативность конъюнкции;

· – ассоциативность дизъюнкции;

· – дистрибутивность конъюнкции относительно дизъюнкции;

· – дистрибутивность дизъюнкции относительно конъюнкции.

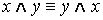
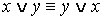
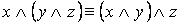
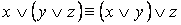
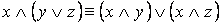
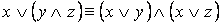
Замечание. Равносильности группы 3 показывают, что над формулами алгебры логики можно проводить те же преобразования, что и в алгебре чисел.

Равносильные преобразования формул

Используя равносильности групп 1–3 можно часть формулы или формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными.

Равносильные преобразования используются для доказательства равносильностей , для приведения формул к заданному виду, для упрощения формул. Формула A считается проще равносильной ей формулы B , если она содержит меньше букв, меньше логических операций. При этом обычно операции эквивалентность и импликация заменяются операциями дизъюнкции и конъюнкции, а отрицание относят к элементарным высказываниям.

Источник

Читайте также:  Как можно вызвать гнома желаний дома днем работающий способ