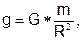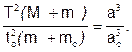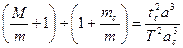Какими способами можно измерить массу небесного тела

§ 58. Определение масс небесных тел

Закон всемирного тяготения Ньютона позволяет измерить одну из важнейших физических характеристик небесного тела — его массу.

Массу небесного тела можно определить: а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ); б) по третьему (уточненному) закону Кеплера; в) из анализа наблюдаемых возмущений, производимых небесным. телом в движениях других небесных тел.

Первый способ применим пока только к Земле и заключается в следующем.

На основании закона тяготения ускорение силы тяжести на поверхности Земли

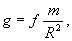
где т — масса Земли, a R — ее радиус. Отсюда масса Земли

Ускорение силы тяжести g (точнее, ускорение составляющей силы тяжести, обусловленной только силой притяжения), так же как и радиус Земли R , определяется из непосредственных измерений на поверхности Земли (см. § 46 и 62). Постоянная тяготения f достаточно точно определена из опытов Кэвендиша и Йолли, хорошо известных в физике.

С принятыми в настоящее время значениями величин g , R и f по формуле (2.25) получается масса Земли

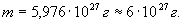
Зная массу Земли и ее объем, легко найти среднюю плотность Земли. Она равна 5,52 г/см 3

Третий, уточненный закон Кеплера позволяет определить соотношение между массой Солнца и массой планеты, если у последней имеется хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг нее.

Действительно, движение спутника вокруг планеты подчиняется тем же законам, что и движение планеты вокруг Солнца и, следовательно, уравнение (2.24) может быть записано в этом случае так:

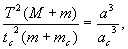
где — М, т и m_c — массы Солнца, планеты и ее спутника, Т и t_c — периоды обращений планеты вокруг Солнца и спутника вокруг планеты, a и а_с — расстояния планеты от Солнца и спутника от планеты соответственно.

Разделив числитель и знаменатель левой части дроби этого уравнения па т и решив его относительно масс, получим

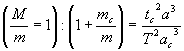
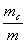
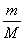
Отношение для всех планет очень велико; отношение же наоборот, мало (кроме Земли и ее спутника Луны) и им можно пренебречь. Тогда в уравнении (2.26) останется только одно неизвестное отношение , которое легко из него определяется. Например, для Юпитера определенное таким способом обратное отношение равно 1 : 1050.

Так как масса Луны, единственного спутника Земли, сравнительно с земной массой достаточно большая, то отношением 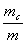в уравнении (2.26) пренебрегать нельзя. Поэтому для сравнения массы Солнца с массой Земли необходимо предварительно определить массу Луны. Точное определение массы Луны является довольно трудной задачей, и решается она путем анализа тех возмущений в движении Земли, которые вызываются Луной.

Под влиянием лунного притяжения Земля должна описывать в течение месяца эллипс вокруг общего центра масс системы Земля — Луна.

По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые “лунным неравенством”. Наличие “лунного неравенства” в видимом движении Солнца указывает на то, что центр Земли действительно описывает небольшой эллипс в течение месяца вокруг общего центра масс “Земля — Луна”, расположенного внутри Земли, на расстоянии 4650 км от центра Земли. Это позволило определить отношение массы Луны к массе Земли, которое оказалось равным 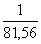. 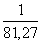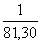Положение центра масс системы “Земля — Луна” было найдено также из наблюдений малой планеты Эрос в 1930—1931 гг. Эти наблюдения дали для отношения масс Луны и Земли величину . Наконец, по возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось равным . Последнее значение наиболее точное, и в 1964 г. Международный астрономический союз принял его как окончательное в числе других астрономических постоянных. Это значение подтверждено в 1966 г. вычислением массы Луны по параметрам обращения ее искусственных спутников.

С известным отношением масс Луны и Земли из уравнения (2.26) получается, что масса Солнца M _¤ в 333 000 раз больше массы Земли, т.е.

Зная массу Солнца и отношение этой массы к массе любой другой планеты, имеющей спутника, легко определить массу этой планеты.

Массы планет, не имеющих спутников (Меркурий, Венера, Плутон), определяются из анализа тех возмущений, которые они производят в движении других планет или комет. Так, например, массы Венеры и Меркурия определены по, тем возмущениям, которые они вызывают в движении Земли, Марса, некоторых малых планет (астероидов) и кометы Энке — Баклунда, а также по возмущениям, производимым ими друг на друга.

Источник

Методы определения масс небесных тел.

Массу можно определить:

а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ),

б) по третьему уточнённому закону Кеплера,

в) из анализа наблюдаемых возмущений, производимых небесным телом в движениях других небесных тел.

1. Первый способ применяется на Земле.

На основании закона тяготения ускорение g на поверхности Земли:

где m — масса Земли, а R — её радиус.

g и R измеряются на поверхности Земли. G = const.

С принятыми сейчас значениями g, R, G получается масса Земли:

m = 5,976 .1027г = 6 .1024кг.

Зная массу и объём, можно найти среднюю плотность. Она равна 5,5 г/см3.

2. По третьему закону Кеплера можно определить соотношение между массой планеты и массой Солнца, если у планеты есть хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг неё.

где M, m, mc- массы Солнца, планеты и её спутника, T и tc- периоды обращений планеты вокруг Солнца и спутника вокруг планеты, а и ас— расстояния планеты от Солнца и спутника от планеты соответственно.

Из уравнения следует

Отношение М/m для всех планет очень велико; отношение же m/mc, очень мало (кроме Земли и Луны, Плутона и Харона) и им можно пренебречь.

Соотношение М/m можно легко найти из уравнения.

Для случая Земли и Луны нужно сначала определить массу Луны. Это сделать очень сложно. Решается задача путём анализа возмущений в движении Земли, которые вызывает Луна.

3. По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые «лунным неравенством». Наличие этого факта в видимом движении Солнца указывает на то, что центр Земли описывает небольшой эллипс в течение месяца вокруг общего центра масс «Земля — Луна», расположенного внутри Земли, на расстоянии 4650 км. от центра Земли.

Положение центра масс Земля-Луна было найдено также из наблюдений малой планеты Эрос в 1930 — 1931 гг.

По возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось 1/81,30.

В 1964 году Международный астрономический союз принял его как const.

Из уравнения Кеплера получаем для Солнца массу = 2.1033г., что в 333000 раза превосходит земную.

Массы планет, не имеющих спутников, определены по возмущениям, которые они вызывают в движении Земли, Марса, астероидов, комет, по возмущениям, производимым ими друг на друга.

Дата добавления: 2014-12-17 ; просмотров: 6750 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

История астрономии

Методы определения масс небесных тел

Массу можно определить:

а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ),

б) по третьему уточнённому закону Кеплера,

в) из анализа наблюдаемых возмущений, производимых небесным телом в движениях других небесных тел.

1. Первый способ применяется на Земле.

На основании закона тяготения ускорение g на поверхности Земли:

где m — масса Земли, а R — её радиус.

где g и R измеряются на поверхности Земли. G = const.

С принятыми сейчас значениями g, R, G получается масса Земли: m = 5,976 . 10 27 г = 6 . 10 24 кг. Зная массу и объём, можно найти среднюю плотность. Она равна 5,5 г/см 3 .

где M, m, m c — массы Солнца, планеты и её спутника, T и t c — периоды обращений планеты вокруг Солнца и спутника вокруг планеты, а и а с — расстояния планеты от Солнца и спутника от планеты соответственно. Из уравнения следует:

Отношение М/m для всех планет очень велико; отношение же m/m c , очень мало (кроме Земли и Луны, Плутона и Харона) и им можно пренебречь. Соотношение М/m можно легко найти из уравнения.

Положение центра масс Земля-Луна было найдено также из наблюдений малой планеты Эрос в 1930 — 1931 гг. По возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось 1/81,30. В 1964 году Международный астрономический союз принял его как const. Из уравнения Кеплера получаем для Солнца массу = 2 . 10 33 г., что в 333000 раза превосходит земную.

Возмущающая сила и возмущающее движение.

Если бы тела двигались вокруг Солнца только под действием его силы притяжения, то движения описывались бы законами Кеплера. Такое движение называется невозмущённым . В реальности все тела Солнечной системы притягиваются друг другом. Отклонения в движениях тел от законов Кеплера называются возмущениями , а реальное движение тел — возмущённым движением .

Возмущения имеют очень сложный характер и их учитывать очень трудно. Значения возмущений невелики, так как общая масса всех планет меньше массы Солнца примерно в 700 раз. Возмущения можно рассматривать как различие между положениями светила при возмущённом и невозмущённом движениях, а возмущённое движение тела представлять как движение по законам Кеплера с переменными элементами орбиты.

Изменения элементов орбиты тела вследствие притяжения его другими телами, помимо центрального, называются возмущениями , или неравенствами элементов . Возмущения элементов делятся на вековые и периодические .

Вековые возмущения тел Солнечной системы зависят от взаимного расположения их орбит, которое в течение очень больших промежутков времени меняется очень мало.

Вековым возмущениям подвержены долгота восходящего узла  и долгота перигелия .

Периодические возмущения зависят от относительного положения тел на орбитах, которое при движении тел по замкнутым орбитам повторяется через определённые промежутки времени. Этим возмущениям подвержены почти все элементы орбит.

Приливы и отливы

Прилив – это любая из циклических деформаций одного астрономического тела, вызванная гравитационными силами другого.

Размеры Земли не бесконечно малы по сравнению с расстоянием до Луны и Солнца. Силы лунного и солнечного притяжения на разные точки Земли неодинаковы. Поэтому появляется возмущающая сила, действующая на различные детали поверхности Земли по-разному. В твёрдых массивах действие силы вызывает натяжение, большие массивы воды же увлекаются силой притяжения и перетекают с места на место. Приливное воздействие на атмосферу выражается в появлении атмосферных потоков.

Водные приливы и отливы известны с давних времён. Географ Страбон (род. — 66 г.) рассказывает, что финикияне хорошо знали о приливах и отливах. В Средиземном море эффект малый, но финикияне проходили через Геркулесовы столбы и наблюдали его в океане. Они указывали, что приливы зависят от фаз Луны и особенно интенсивны в полнолуния и новолуния. Итальянский иезуит Кабео (1585 — 1650) предполагал, что Луна производит на морском дне какое-то спиртное вещество, которое и вызывает прилив. Стевин объяснял прилив притяжением Луны, но горб на обратной стороне Земли объяснял существующей там ещё одной притягивающей точкой. Галилей объяснял приливы центробежной силой, отвергая тяготение. Некоторые исследователи предполагали, что Луна производит изменения в давлении воздуха, что влияет на уровень моря.

Н аиболее верное объяснение явлению приливов и отливов дал Исаак Ньютон, с помощью теории гравитации. Он писал, что Луна оттягивает воду от Земли на одной стороне и оттягивает Землю от воды на другой.

Если земная поверхность со всех сторон покрыта океаном, то каждая капля воды имеет ускорение, пропорциональное квадрату расстояния между частицей и и центром Луны.

Равнодействующая ускорений, сообщаемых твёрдым частицам проходит через центр Земли Т и равна:

Приливное действие Луны

где m — масса Луны, r — расстояние центра Луны от центра Земли.

Для воды океана ускорение в точке А больше, чем  T , а в точке В меньше, чем  T , так как:

где R — радиус Земли.

Относительное ускорение (относительно центра Земли) в точке А равно:

Пренебрегаем малым членом R 2 , и вместо (r — R) оставляем r. Эта разность ускорений направлена от центра Земли.

В точках А и В действие Луны ослабляет силу тяжести на Земной поверхности. В точках F и D действие Луны увеличивает силу земной тяжести.

Действие ускорений в промежуточных точках приводит к тому, что вода в океане стремится на одной половине Земли к точке А, где Луна находится в зените, на другой половине к точке В — где Луна находится в надире. Под действием Луны водная оболочка Земли принимает форму эллипсоида, вытянутого по направлению к Луне. Вблизи точек А и В будет прилив, а у точек F и D — отлив.

За промежуток времени между двумя последовательными кульминациями Луны, равный 24 ч 52 м , приливные выступы обойдут вокруг Земли, и в каждом месте будет по два прилива и два отлива. Под действием солнечного притяжения водная оболочка Земли испытывает приливные силы меньше лунных в 2,2 раза. Солнечные приливы отдельно не наблюдаются, они только изменяют величину лунных приливов. Во время новолуний и полнолуний силы складываются и приливы больше обычных, в квадратуры на лунный прилив приходится солнечный отлив, силы вычитаются и приливы меньше.

В реальности Земля не везде покрыта водой, дно морей и океанов обладает сложным рельефом, приливная волна испытывает большое трение. Момент прилива поэтому не совпадает с моментом кульминации Луны и запаздывает до шести часов. Этот промежуток времени называется прикладным часом .

Высота прилива в Чёрном море равна нескольким сантиметрам, в заливе Фанди на Атлантическом побережье Канады — 18 метрам. Трение приливной волны о твёрдые части Земли вызывает систематическое замедление её вращения. Приливы и отливы сказываются на изменениях атмосферного давления.

Прецессия и нутация земной оси

Вследствие возмущающего действия, оказываемого на вращение Земли телами Солнечной системы, ось вращения Земли совершает в пространстве очень сложное движение. Земля имеет форму сфероида, и поэтому различные части сфероида притягиваются Солнцем и Луной неравномерно.

1. Ось медленно описывает конус, оставаясь всё время наклонённой к плоскости движения Земли под углом около 66 º ,5. Это движение называется прецессионным , период его около 26 000 лет. Оно определяет среднее направление оси в пространстве в различные эпохи.

2. Ось вращения Земли совершает различные мелкие колебания около своего среднего положения, главные из которых имеют период 18,6 года, (этот период есть период обращения узлов лунной орбиты, так как нутация есть следствие действия притяжения Луны на Землю) и называются нутацией земной оси. Нутационные колебания возникают, потому что прецессионные силы Солнца и Луны непрерывно меняют свою величину и направление. Они = 0, когда Солнце и Луна находятся в плоскости экватора Земли и достигают максимума при наибольшем удалении от него. Истинный полюс мира вследствие нутации описывает вокруг среднего полюса сложную кривую. Его движение на небесной сфере совершается приблизительно по эллипсу, большая полуось которого равна 18″,4, а малая 13″,7. Вследствие прецессии и нутации взаимное расположение полюсов мира и полюсов эклиптики непрерывно изменяется.

3. Притяжение планет мало, чтобы вызывать изменения положений земной оси. Но планеты влияют на положение земной орбиты. Изменения положений плоскости эклиптики под воздействием притяжения планет называется планетной прецессией .

Полюс мира, определяемый средним направлением оси вращения Земли, т.е. обладающий только прецессионным движением, называется средним полюсом мира . Истинный полюс мира учитывает и нутационные движения оси. Средний полюс мира вследствие прецессии за 26 000 лет описывает около полюса эклиптики окружность радиусом 23º,5. За один год перемещение среднего полюса мира на небесной сфере составляет около 50″,3. На такую же величину перемещаются на запад и равноденственные точки, двигаясь навстречу видимому годовому движению Солнца. Это явление называется предварением равноденствий . Вследствие этого Солнце попадает в равноденственные точки раньше, чем на то же самое место на фоне звёзд. Полюс мира описывает незамыкающийся круг на небесной сфере. 2000 лет до н.э. полярной звездой была  Дракона, через 12 000 лет полярной станет  Лиры. В начале нашей эры точка весеннего равноденствия находилась в созвездии Овна, а точка осеннего равноденствия в созвездии Весов. Сейчас точка весеннего равноденствия находится в созвездии Рыб, а осеннего в созвездии Девы.

Прецессионное движение полюса мира вызывает изменение координат звёзд с течением времени. Влияние прецессии на координаты:

d/dt = m + n sin  tg ,

где d/dt, d/dt — изменения координат за год, m — годичная прецессия по прямому восхождению, n — годичная прецессия по склонению.

Из-за непрерывного изменения экваториальных координат звёзд, происходит медленное изменение вида звёздного неба для данного места на Земле. Некоторые невидимые ранее звёзды будут восходить и заходить, а некоторые видимые — станут невосходящими. Так, через несколько тысяч лет в Европе можно будет наблюдать Южный Крест, но нельзя будет увидеть Сириус и часть созвездия Ориона.

Прецессия была открыта Гиппархом и объяснена И. Ньютоном.

Задача N тел.

Задача определения четырёх и более тел, притягивающих друг друга по закону Ньютона, ещё более сложна, чем задача трёх тел и в общем виде до сих пор не решена.

Задача N тел в общем виде формулируется следующим образом: “ В пустом пространстве помещено N свободных материальных точек, которые притягиваются друг к другу по закону Ньютона. Заданы их начальные координаты и начальные скорости. Определить последующее движение этих точек” .

Для исследования движений N тел применяется метод вычисления возмущений, позволяющий найти приближённое решение задачи. Сейчас существует целый ряд методов для приближённого решения задачи, позволяющих для каждой конкретной системы тел с заданными конкретными начальными условиями построить траектории движения с любой нужной для практики точностью для любого ограниченного отрезка времени.

На ЭВМ было промоделировано движение пяти внешних планет Солнечной системы за 400 лет — с 1653 по 2060 год. Результаты вычислений совпали с данными наблюдений. Однако конкретные численные методы не могут дать ответы на многие вопросы качественного характера, например:

— Будет ли одно из тел всегда оставаться в некоторой области пространства или сможет удалиться в бесконечность?

— Может ли расстояние между какими-либо двумя из этих тел неограниченно убывать, или, напротив, это расстояние будет заключено в определённых пределах?

— Распадётся ли когда-нибудь Солнечная система, если считать, что она состоит из тел, движение которых возмущается малыми силами со стороны всех остальных небесных тел?

Пьер Симон Лаплас в 1799 — 1825 гг. решал ограниченную задачу о движении планет и их спутников под действием силы тяготения Солнца и их взаимного гравитационного воздействия. Лаплас учёл движения 18 тел. Он считал, что точное движение планет временами нарушается и необходимо внешнее вмешательство, чтобы восстановить порядок. В.И. Арнольд доказал несколько теорем, по которым следует, что Солнечная система не распадётся ещё многие миллионы лет.

Открытие новых планет.

В 1781 году Вильям Гершель открыл новую большую планету Уран, которую раньше принимали за звезду. К 1840 году стало ясно, что орбита Урана отличается от предсказанной по теории Ньютона. В орбите были заметны отклонения от теоретически вычисленной траектории. Было сделано предположение, что, движение Урана возмущает какое-то массивное тело, находящееся за его орбитой.

Ж.Ж. Леверье и Дж.К. Адамс независимо друг от друга вычислили положение этого тела. Адамс дал свои вычисления в Гринвичскую и Кембриджскую обсерватории, но на них не обратили должного внимания. Леверье сообщил о своём открытии в Берлинскую обсерваторию Иоганну Готфриду Галле. Он сразу начал поиски объекта и обнаружил его на расстоянии 1 º от вычисленного. Это оказалась планета Нептун.

В 80-х годах XX столетия на ЭВМ было промоделировано движение пяти внешних планет Солнечной системы за 400 лет — с 1653 по 2060 год. Результаты показали, что за орбитой Плутона нет никакой планеты, заметно возмущающей орбиты уже известных планет. Однако, сам Плутон почти не влияет на орбиту Нептуна из-за своей малой массы. Если за орбитой Плутона находятся такие же маломассивные планеты, то их почти невозможно обнаружить. Возможно, что существует массивное тело, движущееся по сильно вытянутой эллиптической орбите, период обращения которого значительно превосходит рассмотренные 400 лет. Существует предположение, что это тело, находясь на расстоянии около 30 тыс. а.е. от Солнца, имея массу сравнимую с массой Юпитера, постоянно выбивает кометы из Облака Оорта, заставляя их двигаться к центру Солнечной системы.

Какие существуют методы определения масс небесных тел?

Можно ли по третьему закону Кеплера найти массу планеты, у которой нет спутника?

Что такое прилив?

Как часто на Земле бывают приливы?

Что такое прикладной час?

Какая максимальная высота приливной волны?

Чем объясняются приливы и отливы?

Кто впервые правильно объяснил явление приливов и отливов?

Что такое прецессия?

Каков период прецессии?

Что такое нутация?

Каков период нутации?

Что такое предварение равноденствий?

Почему прецессия приводит к изменению экваториальных координат?

Где будет Северный полюс мира через 12 тыс. лет?

Как формулируется задача N тел?

Какие есть трудности при решении задачи N тел?

Какая планета была открыта с помощью учета возмущений в движении другой планеты?

Существуют ли массивные планеты за орбитой Нептуна?

1. Вычислить массу Нептуна относительно массы Земли, зная, что его спутник отстоит от центра планеты на 354 тыс. км и период обращения равен 5 суткам 21 часу.

Ответ : 17,1 массы Земли.

2. Радиус Марса меньше радиуса Земли в 1,88 раза, а средняя плотность меньше в 1,4 раза. Определите ускорение силы тяжести на поверхности Марса, если ускорение силы тяжести на поверхности Земли равно 9,81 м/с 2 .

Ответ : g М  3,6 м/с 2 .

3. Оцените массу Сатурна, зная, что спутник его Титан обращается вокруг планеты с периодом 15,9 сут на среднем расстоянии 1220 тыс. км. Для Луны эти величины равны соответственно 27,3 сут и 384 тыс. км.

Ответ : Масса планеты Сатурн составляет примерно 95 масс Земли.

4. Определите массу планеты Плутон (в массах Земли), зная, что ее спутник Харон обращается вокруг планеты с периодом 6,4 сут на среднем расстоянии 19,6 тыс. км. Для Луны эти величины равны соответственно 27,3 сут и 384 тыс. км.

Ответ : Масса планеты Плутон составляет 0,0024 масс Земли.

5. Путешественники заметили, что по местному времени затмение Луны началось в 5 ч 13 мин, тогда как по астрономическому календарю это затмение должно было состояться в 3 ч 15 мин по гринвичскому времени. Какова долгота их местонахождения?

6. Какое полное затмение (солнечное или лунное) продолжительнее. Почему?

7. Обычно полное солнечное затмение наблюдается в полосе шириной около 200 км и протяженностью приблизительно 10 тыс. км. В среднем на Земле происходит одно полное затмение в год. Оцените, через сколько лет затмение повторяется в одном и том же месте.

8. Полным или кольцеобразным будет для наблюдателя, находящегося на Юпитере, затмение Солнца спутником планеты Ганимедом? Диаметр Ганимеда равен 5000 км, радиус орбиты — 1,0710 6 км, радиус Солнца — 696000 км.

9. Представьте, что сегодня наблюдалось солнечное затмение. Когда примерно можно наблюдать ближайшее лунное затмение?

А . Через неделю.

Б . Через две недели.

Г . Через полгода.

Астрономический календарь. Постоянная часть. М. Наука. 1981.

Кононович Э.В., Мороз В.И. Курс общей астрономии. М., Эдиториал УРСС, 2004.

Воронцов-Вельяминов Б.А. Сборник задач и практических упражнений по астрономии. М. Наука. 1974.

Галузо И.В., Голубев В.А., Шимбалев А.А. Планирование и методика проведения уроков. Астрономия в 11 классе. Минск. Аверсэв. 2003.

Шимбалев А.А. Планеты Солнечной системы. Мн. БГПУ., 2009.

Химический состав солнечной атмосферы;

Потемнение солнечного диска к краю;

Внешние слои солнечной атмосферы: хромосфера и корона;

Радио- и рентгеновское излучение Солнца.

Химический состав солнечной атмосферы;

В видимой области излучение Солнца имеет непрерывный спектр, на фоне которого заметно несколько десятков тысяч тёмных линий поглощения, называемых фраунгоферовыми . Наибольшей интенсивности непрерывный спектр достигает в синезелёной части, у длин волн 4300 — 5000 А. В обе стороны от максимума интенсивность спектра убывает.

Внеатмосферные наблюдения показали, что Солнце излучает в невидимые коротковолновую и длинноволновую области спектра. В более коротковолновой области спектр резко меняется. Интенсивность непрерывного спектра быстро падает, а тёмные фраунгоферовы линии сменяются эмиссионными.

Самая сильная линия солнечного спектра находится в ультрафиолетовой области. Это резонансная линия водорода L  с длиной волны 1216 А. В видимой области наиболее интенсивны резонансные линии Н и К ионизованного кальция. После них по интенсивности идут первые линии бальмеровской серии водорода H  , H  , H  , затем резонансные линии натрия, линии магния, железа, титана, других элементов. Остальные многочисленные линии отождествляются со спектрами около 70 известных химических элементов из таблицы Д.И. Менделеева. Присутствие этих линий в спектре Солнца свидетельствует о наличии в солнечной атмосфере соответствующих элементов. Установлено присутствие на Солнце водорода, гелия, азота, углерода, кислорода, магния, натрия, железа, кальция, др. элементов.

Преобладающим элементом на Солнце является водород. На его долю приходится 70% массы Солнца. Следующим является гелий — 29% массы. На остальные элементы вместе взятые приходится чуть больше 1%.

Наблюдения отдельных деталей на солнечном диске, а также измерения смещений спектральных линий в различных его точках говорят о движении солнечного вещества вокруг одного из солнечных диаметров, называемого осью вращения Солнца.

Плоскость, проходящая через центр Солнца и перпендикулярная к оси вращения, называется плоскостью солнечного экватора. Она образует с плоскостью эклиптики угол в 7 0 15’ и пересекает поверхность Солнца по экватору. Угол между плоскостью экватора и радиусом, проведённым из центра Солнца в данную точку на его поверхности называется гелиографической широтой .

Угловая скорость вращения Солнца убывает по мере удаления от экватора и приближения к полюсам.

В среднем = 14º,4 — 2º,7 sin 2 B, где В — гелиографическая широта. Угловая скорость измеряется углом поворота за сутки.

Сидерический период экваториальной области равен 25 суток, вблизи полюсов он достигает 30 суток. Вследствие вращения Земли вокруг Солнца его вращение кажется более замедленным и равно 27 и 32 суток соответственно (синодический период).

Потемнение солнечного диска к краю

Фотосферой называется основная часть солнечной атмосферы, в которой образуется видимое излучение, имеющее непрерывный характер. Таким образом, она излучает практически всю приходящую к нам солнечную энергию. Фотосфера — это тонкий слой газа протяжённостью в несколько сотен километров, достаточно непрозрачный. Фотосфера видна при непосредственном наблюдении Солнца в белом свете в виде кажущейся его “поверхности”.

При наблюдении солнечного диска заметно его потемнение к краю. По мере удаления от центра, яркость убывает очень быстро. Этот эффект объясняется тем, что в фотосфере происходит рост температуры с глубиной.

Различные точки солнечного диска характеризуют углом , который составляет луч зрения с нормалью к поверхности Солнца в рассматриваемом месте. В центре диска этот угол равен 0, и луч зрения совпадает с радиусом Солнца. На краю  = 90 и луч зрения скользит вдоль касательной к слоям Солнца. Большая часть излучения некоторого слоя газа исходит от уровня, находящегося на оптической глубине 1. Когда луч зрения пересекает слои фотосферы под большим углом , оптическая глубина 1 достигается в более внешних слоях, где температура меньше. Вследствие этого интенсивность излучения от краёв солнечного диска меньше интенсивности излучения его середины.

Уменьшение яркости солнечного диска к краю в первом приближении может быть представлено формулой:

I () = I 0 (1 — u + cos ),

где I () — яркость в точке, в которой луч зрения составляет угол с нормалью, I 0 — яркость излучения центра диска, u — коэффициент пропорциональности, зависящий от длины волны.

Визуальные и фотографические наблюдения фотосферы позволяют обнаружить её тонкую структуру, напоминающую тесно расположенные кучевые облака. Светлые округлые образования называются гранулами, а вся структура — грануляцией . Угловые размеры гранул составляют не более 1″ дуги, что соответствует 700 км. Каждая отдельная гранула существует 5-10 минут, после чего она распадается и на её месте образуются новые гранулы. Гранулы окружены тёмными промежутками. В гранулах вещество поднимается, а вокруг них опускается. Скорость этих движений 1-2 км/с.

Источник