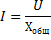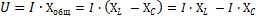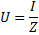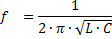Резонанс напряжений

Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.

Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.

Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.

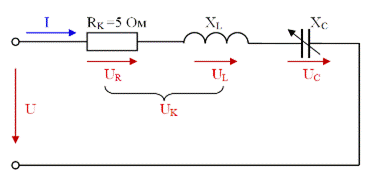
Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки X_L и емкостного сопротивления конденсатора Х_С.

Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:

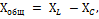
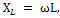
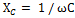
Применив к этой цепи закон Ома, получим:

Формулу эту можно преобразовать следующим образом:

В полученном равенстве I X_L — действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а I Х_С — действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.

Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.

Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:

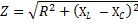
где R — общее активное сопротивление цепи, X_L -Х_С — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать:

Резонанс напряжений в цепи переменного тока

Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.

Иначе говоря, от одновременного действия этих двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.

Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда X_L = Х_С или, что то же, когда ω L = 1 / ωС.

Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома I = U / R , где вместо Z теперь поставлено R.

Одновременно с этим действующие напряжения как на катушке U_L = I X_L так и на конденсаторе Uc = I Х_С окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений .

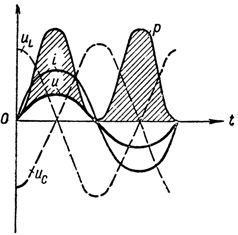
На рис. 1 приведены кривые напряжений, тока и мощности при резонансе напряжений в цепи.

График тока напряжений и мощности при резонансе напряжений

Следует твердо помнить, что сопротивления X_L и Х_С являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как X_L = ω L возрастет, а Х_С = = 1 / ωС уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.

При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.

Действительно, в цепи с одной катушкой индуктивности происходит колебание энергии, т. е. периодический переход энергии из генератора в магнитное поле катушки. В цепи с конденсатором происходит то же самое, но за счет энергии электрического поля конденсатора. В цепи же с конденсатором и катушкой индуктивности при резонансе напряжений (X_L = Х_С) энергия, раз запасенная цепью, периодически переходит из катушки в конденсатор и обратно и на долю источника тока выпадает только расход энергии, необходимый для преодоления активного сопротивления цепи. Таким образом, обмен энергии происходит между конденсатором и катушкой почти без участия генератора.

Стоит только нарушить резонанс напряжений в цени, как энергия магнитного поля катушки станет не равной энергии электрического поля конденсатора, и в процессе обмена энергии между этими полями появится избыток энергии, который периодически будет то поступать из источника в цепь, то возвращаться ему обратно цепью.

Явление это очень сходно с тем, что происходит в часовом механизме. Маятник часов мог бы непрерывно колебаться и без помощи пружины (или груза в часах-ходиках), если бы не силы трения, тормозящие его движение.

Пружина же, сообщая маятнику в нужный момент часть своей энергии, помогает ему преодолеть силы трения, чем и достигается непрерывность колебаний.

Подобно этому и в электрической цепи, при явлении резонанса в ней, источник тока расходует свою энергию только на преодоление активного сопротивления цепи, тем самым поддерживая в ней колебательный процесс.

Итак, мы приходим к выводу, что цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях X_L = Х_С превращается в колебательную систему . Такая цепь получила название колебательного контура.

Из равенства X_L = Х_С можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:

Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений :

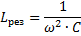
Таким образом, изменяя любую из этих трех величин ( f рез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур.

Пример полезного применения резонанса напряжений : входной контур приемника настраивается конденсатором переменной емкости (или вариометром) таким образом, что в нем возникает резонанс напряжений. Этим достигается необходимое для нормальной работы приемника большое повышение напряжения на катушке по сравнению с напряжением в цепи, созданным антенной.

Наряду с полезным использованием явления резонанса напряжений в электротехнике технике часто бывают случаи, когда резонанс напряжений вреден. Большое повышение напряжения на отдельных участках цепи (на катушке или на конденсаторе) по сравнению с напряжением генератора может привести к порче отдельных деталей и измерительных приборов.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Резонанс напряжений

Резонансом напряжений называется режим электрической цепи синусоидального тока с последовательным соединенением резистивного R, индуктивноо L и емкостного С элементов, при котором угол сдвига фаз между общим напряжением (напряжением сети) и током в цепи равен нулю.

Условием наступления резонанса напряженийявляется равенство индуктивного и емкостного сопротивлений цепи:

Электрическая цепь, питаемая синусоидальным переменным током, в которую входит конденсатор и катушка индуктивности называется колебательным контуром.

Резонанс напряжений можно получить тремя способами:

1. Изменением частоты w синусоидального тока;

2. Изменением величин индуктивности или емкости колебательного контура, при котором меняются индуктивное X_L или емкостное X_C сопротивление;

3. При одновременном изменении параметров w, L, C цепи колебательного контура.

Из условия резонанса напряжения (3.27) следует, что так как

то при резонансе напряжений

, (3.28)

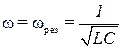
где w_рез, рад/сек – резонансная частота.

Резонанс напряжений характеризуется рядом существенных особенностей:

1. Так как при резонансе напряжений угол сдвига фаз между напряжением и током равен нулю (j = y_u – y_i = 0), то коэффициент мощности при резонансе принимает наибольшее значение, равноеединице:

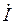
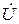
В этом случае, как видно из векторной диаграммы на рис. 3.22,а, вектор тока и вектор общего напряжения совпадают по направлению, так как они имеют равные начальные фазы y_u = y_i.

2. При резонансе напряжений векторы напряжения на индуктивном и емкостном элементах оказываются равными по величине и противоположными по фазе:

так как X_LI = X_CI, а в комплексной форме 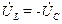(см. рис. 3.22,а).

3. Напряжение на активном сопротивлении при резонансе напряжений оказывается равным напряжению сети (рис. 4.22,а) так как

. (3.31)

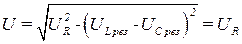
В комплексной форме .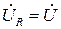

4. Отношение индуктивного или емкостного сопротивлений к активному сопротивлению цепи с R,L,C-элементами при резонансе называется добротностью колебательного контураQ

. (3.32)

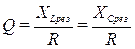
Умножив числитель и знаменатель этих дробей на ток I, получим выражения для добротности колебательного контура через отношения напряжений

. (3.33)

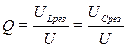
При больших значениях индуктивного X_L и емкостного X_C сопротивлений и малых значениях активного сопротивления R цепи (R > U:

то есть напряжение на индуктивности и конденсаторе последовательного колебательного контура при его высокой добротности в режиме резонанса напряжений могут во много раз превысить напряжение питания.

Например, если у колебательного контура последовательной цепи с
R,L,C-элементами, питаемым синусоидальным напряжением U = 220 В, R = 1 Ом, X_Lрез = X_Cрез = 1000 Ом, то напряжение на индуктивности и конденсаторе, как следует из (3.34) равно:

Поэтому при работе электротехнического оборудования, питаемого сетевым напряжением 220/380 вольт резонанс напряжений никогда не используется.

Однако в разнообразных устройствах радиотехники и электроники, где напряжение питания колебательного контура составляет микровольты
(1мкВ = 10 -6 В), резонанс напряжений широко используется, позволяя многократно усилить входной сигнал в виде синусоидального напряжения.

Рис. 3.22. Резонанс напряжений в цепи с последовательным соединением R,L,C-элементов

а) – векторная диаграмма; б) – вырожденный треугольник сопротивлений (Х = 0);

в) – вырожденный треугольник мощностей (Q = 0)

5. Так как при резонансе напряжений X_L = X_C (3.27), то полное сопротивление цепи принимает минимальное значение, равное активному сопротивлению:

, (3.35)

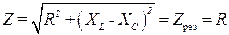
а общее реактивное сопротивление цепи становится равным нулю:

Поэтому треугольник сопротивлений при резонансе напряжений имеет вырожденный характер, как показано на рис. 3.22,б.

6. На основании закона Ома и из формулы (3.35) следует, что ток I в цепи при резонансе напряжений достигает наибольшего значения:

Отсюда следует, что ток в цепи при резонансе напряжений может оказаться значительно больше тока, который мог бы быть при отсутствии резонанса.

Это свойство позволяет обнаружить резонанс напряжений при изменении частоты w, изменении индуктивности L или емкости С. Однако резонансный ток при определенных условиях опасен – он может, достигнув чрезмерно большой величины, привести к перегреву элементов цепи и выходу их из строя.

7. Активная мощность при резонансе напряжений имеет наибольшее значение, так как связана с квадратом тока

8. Общая реактивная мощность Q при резонансе напряжений равна нулю:

так как U_L = U_{C .} Поэтому треугольник мощностей при резонансе имеет вырожденный характер, как показано на рис. 3.22,в.

то есть эти мощности могут во много раз превысить потребляемую полную мощность S. При этом полная мощность S при резонансе целиком выделяется на резистивном элементе R, в виде активной мощности Р.

Физически это объясняется тем, что при резонансе напряжений происходит периодический обмен энергии магнитного поля в индуктивном элементе и энергии электрического поля в конденсаторе. При этом интенсивность этого обмена, как величины реактивных мощностей Q_L и Q_C , в сравнении с потребляемой активной мощностью Р

определяется соотношениями реактивных и активного сопротивления цепи, как и для напряжений U_L, U_C и U, то есть добротностью Q колебательного контура цепи (см. п.4).

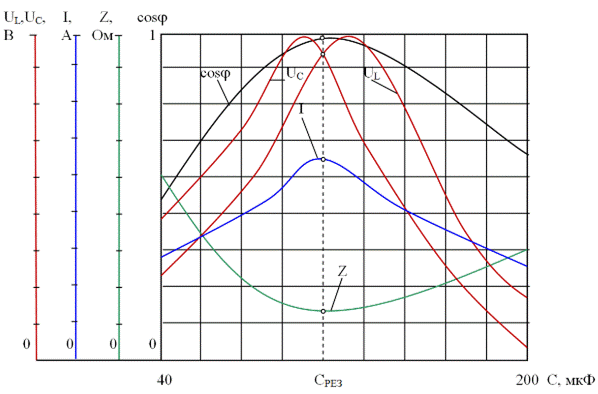
Кривые, выражающие зависимость полного тока I, сопротивления цепи Z, напряжения на индуктивности U_L и конденсаторе U_С , коэффициента мощности cosj от емкости батареи конденсатора С, называются резонансными кривыми.

На рис. 3.23 приведены резонансные кривые (U_L, U_С, I, Z, cosj) = f(C), построенные в общем виде при U = const и w = 2pf = const.

Рис. 3.23. Резонансные кривые U_L , U_С , I , Z, cosj в зависимости от емкости С
при последовательном соединении катушки индуктивности и батареи конденсаторов

Анализ этих зависимостей показывает, что при увеличении емкости С батареи конденсаторов полное сопротивление цепи Z сначала уменьшается, достигает минимума в режиме резонанса и становится равным активному сопротивлению R , а затем снова возрастает с увеличением емкости. Соответственно изменению Z меняется полный ток цепи (по закону Ома I обратно пропорционален Z): с ростом емкости конденсаторов ток I вначале увеличивается, достигает максимума в режиме резонанса, а затем вновь уменьшается.

Коэффициент мощности cosj изменяется с изменением емкости С в том же порядке: сначала с увеличением емкости С коэффициент мощности возрастает, достигая максимума равного единице в режиме резонанса, а затем уменьшается, в пределе стремясь к нулю.

Напряжения на индуктивности и конденсаторах имеют максимумы вблизи режима резонанса и становятся равными друг другу в этом режиме. Следует отметить, что достигаемые величины напряжений на конденсаторах и катушке индуктивности в режиме резонанса напряжений и вблизи него могут во много раз превышать входное напряжение приложенное ко всей цепи (см. п. 4).

С точки зрения электробезопасности и безаварийного режима работы, это следует учитывать при проведении исследования резонанса напряжения на стенде, задавая величину напряжения питания цепи U в достаточно низких пределах (U = 20 ¸ 25 В).

Таким образом, резонансные кривые позволяют установить минимальное полное сопротивление и наибольший ток в цепи при максимуме коэффициента мощности, равном единице, когда в цепи с последовательным соединением катушки индуктивности и батареи конденсаторов возникает резонанс напряжений.

Выводы:

1. Резонанс напряжений в промышленных электротехнических установках, питаемых синусоидальным сетевым напряжением 220/380 В – нежелательное и опасное явление, так как может вызвать аварийную ситуацию при возможном перенапряжении на отдельных участках цепи, привести к пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов и опасно для обслуживающего персонала.

2. В то же время, резонанс напряжений широко используется в радиотехнике, в автоматике и электронике для настройки колебательных контуров в резонанс на определенную частоту, а также в различного рода приборах и устройствах, основанных на резонансном явлении.

Содержание работы

Лабораторная работа 2б делится на четыре части:

1. Подготовительная часть.

2. Измерительная часть (проведение опытов и снятие показаний приборов).

3. Расчетная часть (определение расчетных величин по формулам).

4. Оформительская часть (построение векторных диаграмм).

Примечание

Электромонтажные работы по исследованию резонанса напряжений в цепи с последовательным соединением R,L,C-элементов на модернизированном лабораторном стенде ЭВ-4 не проводятся, в отличие от работ на старых стендах (см. в [2] – Работа 2б, п.2. Электромонтажная часть).

1. Подготовительная часть

Подготовка к проведению лабораторной работы включает:

1. Изучение теоретической части настоящего пособия и литературы [1,2,3,4], относящихся к теме данной работы.

2. Предварительное оформление лабораторной работы в соответствии с существующими требованиями [2,3].

В результате предварительного оформления лабораторной работы №2б в рабочей тетради или журнале (на листах формата А4 с компьютерной распечаткой) студентом должен быть заполнен титульный лист, в работе должны быть указаны название работы и ее цель, приведены основные сведения по работе, взятые из раздела выше и формулы, необходимые для вычисления расчетных величин, представлены принципиальные и эквивалентные схемы замещения, заготовлены таблицы, соответственно числу опытов в работе.

Кроме этого, должно быть оставлено свободное место для построения векторных диаграмм.

2. Измерительная часть

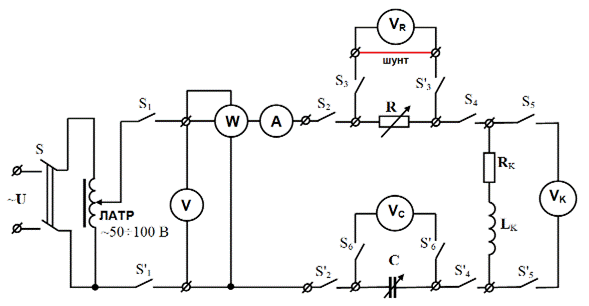
Необходимые измерения параметров исследуемой цепи однофазного тока с последовательным соединением электроприемников при резонансе напряжений проводятся с помощью принципиальной схемы (рис. 3.24). Данная схема соответствует панели модернизированног стенда ЭВ-4 [4] с аналогичной мнемосхемой и цифровыми измерительными приборами (см. фото на рис. 3.26).

Для более заметного вида резонансных кривых в последовательной цепи электроприемников резистор R отсутствует (на принципиальной схеме рис. 3.23 он зашунтирован).

Этой схеме соответствует схема замещения с последовательно соединенными катушкой индуктивности и батареей конденсаторов, показанная на рис. 3.25.

3.24 Принципиальная схема цепи с последовательно соединенными
катушкой индуктивности и батареей конденсаторов
для исследования резонанса напряжений

3.25 Схема замещения цепи с последовательно соединенными
катушкой индуктивности и батареей конденсаторов
для исследования резонанса напряжений

1. Перед подачей питания к исследуемой цепи на панели стенда с мнемосхемой и цифровыми измерительными приборами (рис. 3.26) перевести все выключатели (S₁ ÷ S₆, S’₁ ÷ S’₆), расположенные на этой панели, в нижнее положение (состояние – «откл»).

Рис. 3.26. Паналь стенда с цифровыми измерительными приборами и
мнемосхемой для проведения лабораторой работы 2б «Резонанс напряжений
в однофазной цепи с активно-реактивными элементами»

2. На панели стенда из последовательной цепи R,L,C-элементов исключить резистор R, зашунтировав его с помощью электромонтажного провода (красный провод-шунт на принципиальной схеме рис. 3.24) вставив его концы в гнезда по бокам вольтметра V_R.

3. Установить начальную общую емкость конденсаторов С = 40 мкФ нажатием соответствующих черных кнопок выключателей рядом с подключаемыми конденсаторами на панели №4 стенда с мнемосхемой батареи конденсаторов (см. рис. 3.28).

4. Подключить лабораторный автотрансформатор (ЛАТР), установленный на горизонтальной панели блока питания (рис. 3.27) к сетевому напряжению (

220 В), нажав черные кнопки «вкл» выключателей. При этом загораются две сигнальные лампы «сеть». После этого нужнообязательноповернуть ручку регулятора ЛАТРАа против часовой стрелки до упора, тем самым, снизив напряжение на его выходе до нуля.

Рис. 3.27. Панель блока питания лабораторного стенда

Рис. 3.28. Панель №4 стенда с мнемосхемами батареи конденсаторов
и катушки индуктивности

5. Подать регулируемое напряжение от ЛАТРа ко входу исследуемой цепи и подключить цифровые измерительные приборы, установив на панели стенда с мнемосхемой кнопки всех выключателей (S₁ ÷ S₆, S’₁ ÷ S’₆) в положение «вкл». При этом должны засветиться зеленые цифры на электроизмерительных приборах.

6. Плавным поворотом по часовой стрелке ручки регулятора ЛАТРа (рис. 3.27) установить напряжение U на входе цепи порядка 20 ÷ 25 В, контролируя его цифровым вольтметром V (прибор ЩП02М, установленный слева на панели стенда – рис. 4.26). Следует поддерживать установленное напряжение постоянным во всех опытах с помощью ЛАТРа.

7. В процессе исследования цепи с последовательно соединенными катушкой индуктивности и батареей конденсаторов провести 9 опытов с различной емкостью батареи конденсаторов (величины емкостей для каждого опыта указаны в табл. 3.5) нажатием соответствующих кнопок выключателей на панели №4 стенда (рис. 3.28), постепенно увеличивая емкость с 40 мкФ до 200 мкФ. Перед подключением дополнительных конденсаторов в каждом опыте нужно обязательно отключить исследуемую цепь от источника питания (выхода ЛАТРа), переведя выключатели (S₁, S’₁) в нижнее положение «откл», а перед проведением замеров вновь подключить к напряжению питания цепь с помощью тех же выключателей.

8. Во всех опытах измерить входное напряжение U, потребляемую активную мощность Р и протекающий по цепи ток I, соответственно цифровыми измерительными приборами: вольтметром V, ваттметром W и амперметром А (см. принципиальную схему на рис. 3.24 и панель стенда на рис. 3.26).

9. Напряжение на батарее конденсаторов U_С и напряжение на катушке индуктивности U_К с параметрами R_K, L_K измерить цифровыми вольтметрами, соответственно V_C и V_K, установленными на панели стенда (см. рис. 3.26).

10. Полученные результаты измерений каждого опыта занести в таблицу 3.5.

11. В конце измерительной части данной работы нужно отключить исследуемую цепь от источника питания и сам блок питания от силового щитка с помощью выключателей S₁ и S₁ ‘ на панели с мнемосхемой (рис. 3.26) и красной кнопки «выкл» выключателя на панели блока питания (рис. 3.27). Сообщить преподавателю об окончании измерений и приступить к вычислениям параметров цепи.

Источник