Объем тела, его измерение.
Объем– это положительная скалярная величина, характеризующая размер геометрического тела.
Объемом тела называется положительная скалярная величина, определенная для каждого геометрического тела так, что:
1. равные тела имеют равные объемы;2. если тело составлено из нескольких тел, то его объем равен сумме их объемов.
Будем объем тела Q обозначать V(Q).Чтобы измерить объем тела, нужно выбрать единицу объема. Таковой является куб со стороной, равной единице длины, его объем равен е3. Измерение объема состоит в сравнении объема данного тела с объемом единичного куба. Результатом этого сравнения является такое число х такое, что V(Q) = х ∙ е3, которое называют численным значением объема при данной единице объема.Свойства численных значений объема1. Если тела равны, то равны и численные значения их объемов:
Q1 = Q2 
V(Q1) = V(Q2). 2. Если тело Q состоит из тел Q1, Q2,…, Qn, то численное значение объема тела равно сумме численных значений объемов этих тел. 3. При замене единицы измерения объема численное значение объема увеличивается (уменьшается) во столько раз, во сколько раз уменьшается (увеличивается) единица объема. Выразим, например, 9 дм3 в кубических сантиметрах. Известно, что 1 дм3 = 1000 см3, и, следовательно, 9 дм3 = 9 ∙ 1 дм3 = 9 ∙ (1000 см3) = (9 ∙ 1000) ∙ см3 = = 9000 см3.
Для измерения объемов площадей используют стандартные единицы площади: м3, дм3, см3, мм3. Основная единица измерения объема – кубический метр. Соотношения между единицами объема: 10-9 км3 = 1м3 = 103дм3 = 106 см3 = 109 мм3. В начальной школе рассматривается объем прямоугольного параллелепипеда. Рассмотрим случай, когда длина, ширина и высота выражены натуральными числами. Если стороны основания равны а и b, то на это основание можно уложить а ∙ b единичных кубиков. Так как в высоту укладывается с таких слоев, то объем параллелепипеда вычисляется по формуле V = а ∙ b∙ с. Таким образом объем прямоугольного параллелепипеда равен произведению трех его измерений. В начальной школе изучается также такая величина, как емкость. Она рассматривается как объем сыпучих и жидких тел. Единица измерения емкости – литр. 1 л = 1 дм3. Измерить объемы тел более трудно, чем площадь фигур. Приведем несколько способов измерения объемов. 1. Правило Архимеда. Объем воды, вытесненной телом при погружении, равен объему этого тела. 2. Косвенный способ измерения объема. · Посредством измерения длин сторон и других отрезков и нахождения площади с помощью формул. · Нахождение объем через массу и плотность тела. 3. Метод дополнения (разбиения).
4. Объем (емкость) сосудов – с помощью наполнения.
Масса, ее измерения.
Определение. Массой тела называется положительная величина, определенная для каждой фигуры так, что: 1) масса одинакова у тел, уравновешивающих друг друга на весах; 2) масса складывается, когда тела соединяются вместе: масса нескольких тел, взятых вместе, равна сумме их масс. Измерение массы производится с помощью весов. Выбираем тело е, масса которого принимается за единицу. Предполагается, что можно взять и доли этой массы. Например, если за единицу массы взят килограмм, то в процессе измерения можно использовать и такую его долю, как грамм: 1 г = 1/1000 кг. На одну чашку весов кладут тело, массу которого измеряют, а на другую – тела, выбранные в качестве единицы массы, т.е. гири. Этих гирь должно быть столько, чтобы они уравновесили первую чашку весов. В результате взвешивания получается численное значение массы данного тела при выбранной единице массы. Это значение приближенное. Например, если масса тела равна 5 кг 350 г, то число 5350 следует рассматривать как приближенное значение массы данного тела (при единице массы – грамм). Для численных значение массы справедливы все утверждения, сформулированные для длины, т.е. сравнение масс, действия над ними сводятся к сравнению и действиям над числовыми значениями масс (при одной и той же единице массы). Основная единица массы – килограмм. Из этой основной единицы образуются другие единицы массы: грамм, тонна и др.
Источник
ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1 . Определите цену деления мензурки.
2 . Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3 . Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201 ), и снова измерьте объём жидкости.
4 . Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5 . Результаты измерений запишите в таблицу 9 .
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202 ). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.
Таблица 9 . 
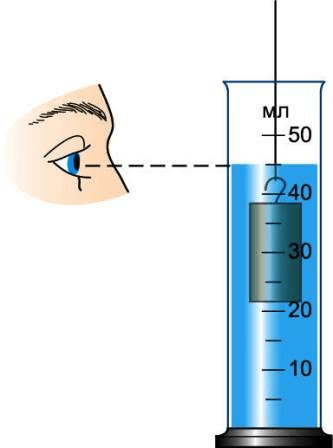
рис. 201
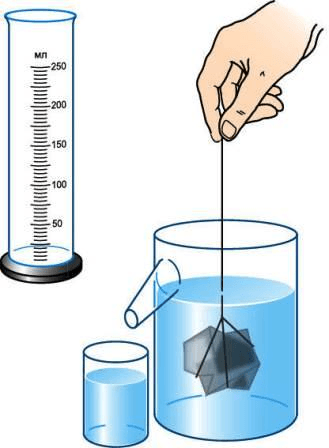
рис. 202
Решение
Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэтому для измерения объема воспользуемся мензуркой. Тело, полностью погружённое в жидкость, вытесняет объём жидкости, который равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следующим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
$V = V_ <2>— V_<1>$ , где $V_<2>$ − объём воды и тела, $V_<1>$ − начальный объём воды в мензурке.
- Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
Таким образом, цена каждого деления будет равна
$\frac<30 - 20><2>= \frac<10><2>$ = 5 мл. - В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70 $см^<3>$ .
- Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
Вычисления.
$V_ <бр>= 95 — 70 = 25 см^<3>$
$V_ <ц>= 85 — 65 = 20 см^<3>$
$V_ <ш>= 75 — 60 = 15 см^<3>$ - Результаты измерений запишем в таблицу 9 .
| № опыта | Название тела | Начальный объём воды в мензурке $V_<1>, см^<3>$ | Объём воды и тела $V_<2>, см^<3>$ | Объём тела V, $см^<3>$ $V = V_<2>-V <1>$ |
|---|---|---|---|---|
| 1 | Брусок | 70 | 95 | 25 |
| 2 | Цилиндр | 65 | 85 | 20 |
| 3 | Шарик | 60 | 75 | 15 |
Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.
Источник
Лекция 13. Объем геометрического тела и его измерение.
Лекция 13. Объем геометрического тела и его измерение.
Объем– это положительная скалярная величина, характеризующая размер геометрического тела.
Объемом тела называется положительная скалярная величина, определенная для каждого геометрического тела так, что:
1. равные тела имеют равные объемы;
2. если тело составлено из нескольких тел, то его объем равен сумме их объемов.
Будем объем тела Q обозначать V(Q).
Чтобы измерить объем тела, нужно выбрать единицу объема. Таковой является куб со стороной, равной единице длины, его объем равен е 3 . Измерение объема состоит в сравнении объема данного тела с объемом единичного куба. Результатом этого сравнения является такое число х такое, что V(Q) = х ∙ е 3 , которое называют численным значением объема при данной единице объема.
Свойства численных значений объема
1. Если тела равны, то равны и численные значения их объемов:
2. Если тело Q состоит из тел Q 1 , Q 2 ,…, Q n , то численное значение объема тела равно сумме численных значений объемов этих тел.
3. При замене единицы измерения объема численное значение объема увеличивается (уменьшается) во столько раз, во сколько раз уменьшается (увеличивается) единица объема.
Выразим, например, 9 дм 3 в кубических сантиметрах. Известно, что 1 дм 3 = 1000 см 3 , и, следовательно, 9 дм 3 = 9 ∙ 1 дм 3 = 9 ∙ (1000 см 3 ) = (9 ∙ 1000) ∙ см 3 = = 9000 см 3 .
Для измерения объемов площадей используют стандартные единицы площади: м 3 , дм 3 , см 3 , мм 3 . Основная единица измерения объема – кубический метр. Соотношения между единицами объема: 10 -9 км 3 = 1 м 3 = 10 3 дм 3 = 10 6 см 3 = 10 9 мм 3 .
Объем прямоугольного параллелепипеда равен произведению трех его измерений. 
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту. 
Объем прямой призмы равен произведению площади основания на высоту.
Объем наклонной призмы равен произведению площади основания на высоту.
Объем пирамиды равен одной трети произведения площади основания на высоту.
Объем прямого цилиндра равен произведению площади основания на высоту.
Объем конуса равен одной трети произведения площади основания на высоту.
Объем усеченного конуса, высота которого равна 
, а площади оснований 
и 
, вычисляется по формуле 
.
Объем шара радиуса равен. 
Задания для самостоятельной работы по теме:
Ребро данного куба равно 1/3 ребра единичного куба. Чему равен объем данного куба?
Найдите объем правильной четырехугольной пирамиды, сторона которого 5см., а высота 8 см.
Источник
Измерение объема. Единицы объема
Разделы: Физика
Демонстрационный виртуальный эксперимент впервые предоставляет ученику реальную возможность зрительно познакомиться с изучаемым физическим явлением и выяснить устройство и принцип действия приборов, машин и различных устройств. Здесь ещё нет элементов исследования, изменения параметров физических величин, моделирования различных ситуаций – это всё будет потом, в других видах физического виртуального эксперимента. А сейчас надо увлечь ученика, или, говоря высоким стилем, усилить его мотивацию. В связи с этим к демонстрационным программам предъявляются серьёзные требования: они должны быть педагогически целесообразными, выразительными, интересными и доступными как для слабых, так и для сильных учащихся. Соответствующие программы позволяют демонстрировать различные физические явления, выяснять устройство и принцип действия приборов, машин и различных устройств. Они помогают ученику сделать первый шаг в изучении того или иного физического явления или физического прибора.
Тип урока: урок изучения нового материала.
Цели урока: выяснить способы измерения объемов тел, изучить приборы для измерения объемов тел, открыть возможности измерения для решения задач.
Задачи по воспитанию и развитию учащихся:
Оборудование: IBM PC – 10 шт. (компьютерный класс), мультимедийный проектор; оборудование для эксперимента: мензурки, бруски разных размеров, вода, прибор Архимеда.
Методическое обеспечение: 1) презентация, 2) флэш-анимации “Правила измерений”, “Определение цены деления мензурки”, “Измерение объемов неправильной формы”; 3) карточки-конспекты; 4) карточки с условиями качественных задач; 5) карточки, предназначенные для самоконтроля учеников; 6) карточки с домашним заданием.
I. Организационно-мотивационный этап.
Чему бы ты не учился, ты учишься для себя. (Гай Петроний)
Надо много учиться, чтобы знать хоть немного. (Монтескьё)
Учитель спрашивает мнение учащихся о высказываниях философов. Спрашивает: какое отношение имеют данные высказывания к нашему уроку? Затем сообщает, что на уроке их ждёт много нового.
II. Актуализация опорных знаний. Приложение 1.
2) Групповая работа. Игра “Сгруппируй приборы измерения”.
На карточках различные приборы. Приложение 2. Ученики сортируют их по группам.
Учитель. На сколько групп вы разделили приборы измерений? Правильно, три. Скажите, для измерения какой физической величины необходимы приборы каждой группы?
Ученики. Линейки и мерные ленты для измерения длины, термометры для измерения температуры, мензурки, пробирки для измерения объема.
Учитель. Молодцы, ребята! Сегодня на уроке мы с вами познакомимся с разными способами измерения объемов тел, а также с единицами объема.
III. Изучение нового материала. Измерение объема. Единицы объема.
1) Измерение объема прямоугольного параллелепипеда.
Величина части пространства, занимаемого геометрическим телом, называется объемом этого тела.
Английские меры объема
Бушель — 36,4 дм 3
Галлон — 4,5 дм 3
Баррель (сухой) — 115,628 дм 3
Баррель (нефтяной) — 158,988 дм 3
Английский баррель для сыпучих веществ — 163,65 дм 3
Русские меры объема
Бочка — 490 дм 3
Штоф — 1,23 дм 3 = 10 чарок
Чарка — 0,123 дм 3 =0,1 штофа= 2 шкалика
Шкалик — 0,06 дм 3 = 0,5 чарки
! Объем прямоугольного параллелепипеда равен произведению трех его измерений.
V = abc (1 способ)
! 2) Основная единица измерения объема – метр кубический.
Дольные единицы м 3 :
1 м 3 = 1000 дм 3 =1000000 см 3 = 1000000000 мм 3
1 м 3 = 10 3 дм 3 =10 6 см 3 = 10 9 мм 3
1 л = 1 дм 3 = 0,001 м 3
1 см 3 = 0,001 дм 3 = 0,000001 м 3 = 10 -6 м 3
1 мм 3 = 0,001 см 3 = 0,000001 дм 3 = 0,000000001 м 3 = 10 -9 м 3
Приложение 3. Измерение объема. Единицы объема. (Карточка для учащихся)
3) Приборы для измерения объема. Правила измерений.
б) мерные пробирки;
в) мерные емкости и др.
3) Определение цены деления шкального прибора. Виртуальная демонстрация. Приложение 4.
4) Правила измерений. Виртуальная демонстрация. Приложение 5.
V. Закрепление нового материала. Практическая работа. Приложение 6.
Практическая работа разбита на 2 варианта и 3 уровня: – 1-ый уровень, – 2-ой уровень, – 3-ий уровень. Первые 2 задания ученики выполняют по карточкам-рисункам, а третье задание выполняют на компьютерах с помощью анимационной модели (Приложение 7).
Пример практического задания.
Уровень 2. Вариант 2
- Определите объем жидкостей в мензурках 1, 2 и 3.
Определите объем тела неправильной формы.
1. Как называется прибор, изображенный на рисунке?
- колба,
- мензурка,
- Архимедова колба,
- отливной сосуд.
2. Определите цену деления мензурки.
Определите объем налитой жидкости.
3. Площадь листа жести равна 90 см 2 . Выразите её в дм 2 и м 2 .
4. В канистру налито 5 л бензина. Выразите данный объем в дм 3 и м 3 .
5. Рассчитайте количество кирпичей, которое пошло на строительство стены высотой 2,4 м, шириной 40 см и длиной 50 дм, если объем одного кирпича равен 2400 см 3 .
Ответы: 1) в, г; 2) 5 мл, 15 мл; 3) 90 см 2 = 0,9 дм 2 = 0,009 м 3 ; 4) 5 л = 5 дм 3 = 0,005 м 3 ; 5) 24 дм · 4 дм · 50 дм / 2,4 дм 3 = 2000 шт.
VII. Домашнее задание.
Параграф 11, упражнение 7, задания на карточках по вариантам (Приложение 9). По желанию учащихся можно выполнить виртуальную лабораторную работу “Измерение объема тела с помощью мерного цилиндра и отливного сосуда”.
Пример задания на карточке.
Задание: определите цену деления мензурки, объем тела.
VIII. Рефлексия. Подведение итогов урока.
Учитель. Ребята! Давайте вспомним, о чем мы с вами говорили в начале урока? (Эпиграф, цели урока). Как вы считаете? Научились ли Вы чему-нибудь на уроке? Что нового узнали? Что вас заинтересовало? Что еще нужно повторить на следующем уроке? О чем вы сможете рассказать своему близкому другу после сегодняшнего урока? Кто работал на уроке лучше всех? Кого Вы считаете еще нужно отметить за хорошую работу на уроке?
Выставление отметок учащимися своим одноклассникам.
До встречи на следующем уроке!
Приложение 11. Презентация к уроку.
Источник
