Какими могут быть колонны по способу приложения нагрузки

НАГРУЗКИ ПО СПОСОБУ ПРИЛОЖЕНИЯ

По способу приложения нагрузки бывают объемными (собственный вес, силы инерции), действующими на каждый бесконечно малый элемент объема, и поверхностными. Поверхностные нагрузки делятся на сосредоточенные нагрузки и распределенные нагрузки.

Распределенные нагрузки характеризуются давлением — отношением силы, действующей на элемент поверхности по нормали к ней, к площади данного элемента и выражаются в Международной системе единиц (СИ) в паскалях, мегапаскалях (1 ПА = 1 Н/м2; 1 МПа = 106 Па) и т.д., а в технической системе – в килограммах силы на квадратный миллиметр и т.д. (кгс/мм2, кгс/см2).

В сопромате часто рассматриваются поверхностные нагрузки, распределенные по длине элемента конструкции. Такие нагрузки характеризуются интенсивностью, обозначаемой обычно q и выражаемой в ньютонах на метр (Н/м, кН/м) или в килограммах силы на метр (кгс/м, кгс/см) и т.д.

НАГРУЗКИ ПО ХАРАКТЕРУ ИЗМЕНЕНИЯ ВО ВРЕМЕНИ

По характеру изменения во времени выделяют статические нагрузки — нарастающие медленно от нуля до своего конечного значения и в дальнейшем не изменяющиеся; и динамические нагрузкивызывающие большие силы инерции.

Вопрос

1. Брус — любое тело, у которого длина значительно больше других размеров.

В зависимости от форм продольной оси и поперечных сечений различают несколько видов брусьев:

— прямой брус постоянного поперечного сечения (рис. 4.4, а);

— прямой ступенчатый брус (рис. 4.4, 6);

— криволинейный брус (рис. 4.4, в).

2. Пластина — любое тело, у которого толщина значительноменьше других размеров (рис.4.5).

3. Массив — тело, у которого три размера одного порядка.

Вопрос

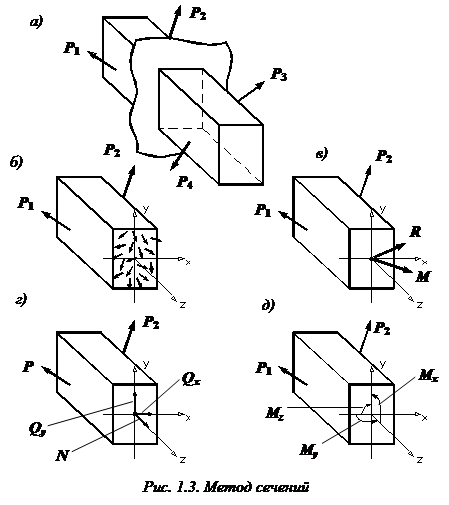
Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.

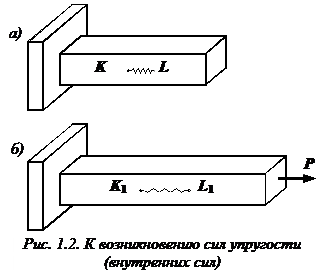
Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).

Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.

Приложим теперь к стержню растягивающую силу (рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение , а частица L – в положение . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и Lблагодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.

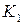
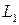
ВНУТРЕННИЕ СИЛЫ В МЕТОДЕ СЕЧЕНИЙ

Полученную бесконечную систему сил по правилам теоретической механики можно привести к центру тяжести поперечного сечения. В результате получим главный вектор R и главный момент M (рис. 1.3, в).

Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.

Получим 6 внутренних силовых факторов, возникающих в поперечном сечении стержня при его деформировании: три силы 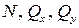(рис. 1.3, г) и три момента (рис. 1.3, д).

Сила N — продольная сила

– поперечные силамы,

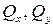
момент относительно оси z ( 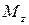) – крутящий момент

моменты относительно осей x, y ( 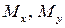) – изгибающие моменты.

Запишем для оставленной части тела уравнения равновесия (уравновесим):

.

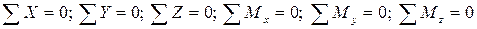
Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.

Вопрос

Переменное напряжение

Напряжения, переменные во времени, возникающие в элементах конструкции под действием нагрузок, переменных по величине или направлению, а также нагрузок, перемещающихся относительно рассматриваемого элемента.

Допускаемое напряжение

Экспериментально установленное для рассматриваемого материала предельное значение напряжения, деленное на коэффициент запаса прочности.

Главное напряжение

Среди множества площадок, которые можно провести через исследуемую точку, имеются три взаимно перпендикулярные площадки, касательные напряжения на которых отсутствуют. Эти площадки и возникающие на них нормальные напряжения называются главными.

Источник

Классификация типов колонн и области их применения

Колонны, одни из основных элементов каркаса производственного здания и других конструктивных комплексов, могут быть цен­трально- и внецентренно сжатыми (зависит от способа их загруже­ния). Центрально-сжатые колонны применяются для поддержания междуэтажных перекрытий и покрытий зданий, в рабочих площад­ках, путепроводах, эстакадах и т. п. Внецентренно сжатые колонны устраивают в каркасах производственных зданий.

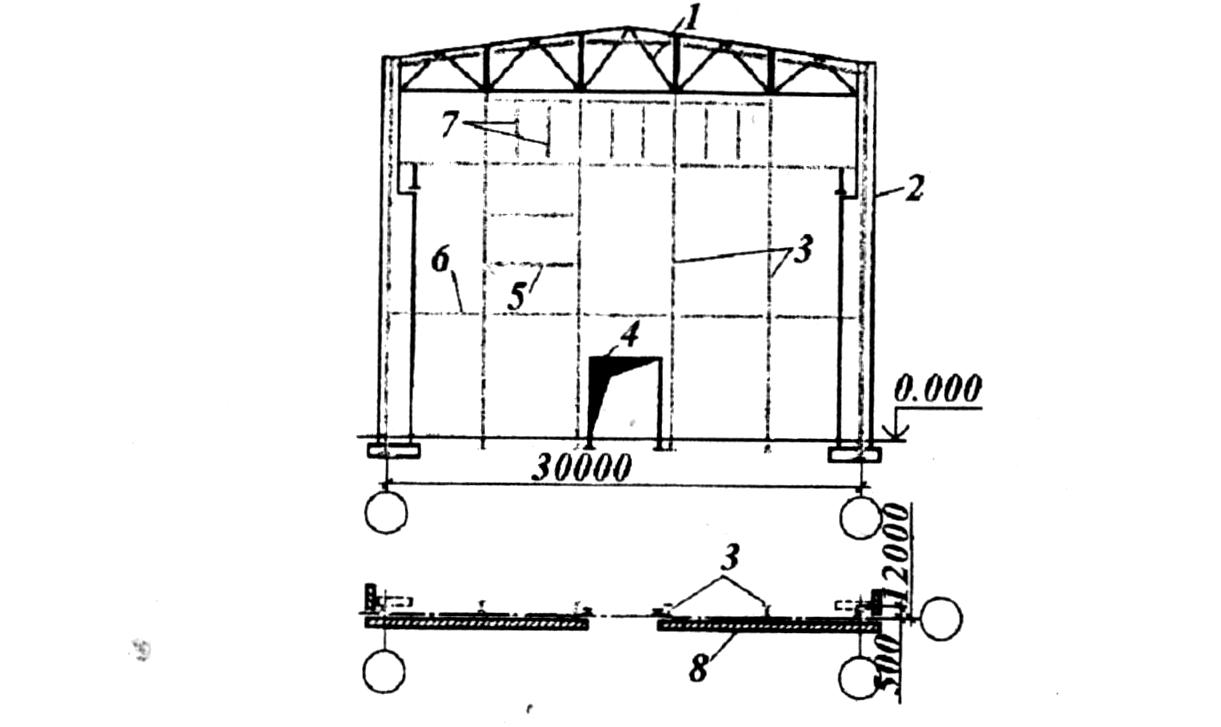
Колонны состоят из следующих основных элементов (рисунок ниже): стержень (ствол) 4 — основной несущий элемент; оголовок 5, на который опирается вышележащая конструкция, нагружающая ко­лонну; база 3, передающая давление от стержня на фундамент 2 и закрепляющая колонну в фундаменте.

В бескрановых зданиях и зданиях, оборудованных подвесными кранами, колонны имеют постоянное по высоте сечение (рисунок ниже). При использовании в производственных зданиях мостовых кранов от­носительно небольшой грузоподъемности (до 15 т) также применяют колонны постоянного сечения, причем нагрузка от кранов передается на стержень колонны через консоли, на которые опираются подкрано­вые балки (рисунок ниже). При мостовых кранах значительной грузоподъ­емности устраивают ступенчатые колонны (рисунок ниже), в которых подкрановые балки опираются на уступ нижнего участка колонны и располагаются по оси подкрановой ветви.

Конструкция торцевого фахверка

Типы колонн

а — сплошная постоянного сечения; б, в — то же, сквозные; г — сплошная постоянного сечения с консолью для подкрановой балки; д — сквозная ступенчатая для крайнего ряда; е — то же, для среднего ряда; 1 — расчетная схема; 2 — фундамент; 3 — база; 4 — стержень; 5 — оголовок

По конструкции колонны могут быть сплошного (рисунок выше) или сквозного сечения (рисунок выше). Преимущество сквозных колонн перед сплошными заключается в том, что, назначая соответствующее рас­стояние между ветвями, можно получить колонну, равноустойчивую относительно обеих главных осей как при одинаковых расчетных (приведенных) длинах l_Х= l_У, так и при резко различных. Это обеспе­чивает более эффективное использование материала ветвей и, соот­ветственно, меньший вес сквозных колонн. Однако изготовление сквозных колонн более сложно, трудоемко и поэтому дороже.

Составные стержни (сплошные и сквозные), аналогичные по конструкции и работе колоннам, также используют в гидротехни­ческих затворах, для мачт, стрел, башенных опор, в качестве эле­ментов тяжелых решетчатых ферм.

Источник

Расчетные ситуации и сочетания нагрузок при расчете колонн. Учимся анализировать.

Колонны в основном рассчитываются как внецентренно сжатые элементы. Что это значит? Если на колонну действует просто вертикальная сила, причем эта сила приложена ровно в центре колонны, то такая колонна фактически работает лишь на сжатие. Сжимающее усилие железобетон выдерживает очень хорошо. Мы знаем, что расчетное сопротивление бетона класса В25 осевому сжатию Rb = 148 кг/см2. Что это значит? Что каждый квадратный сантиметр бетона колонны (или другого сжатого элемента из бетона кл. В25) может выдержать нагрузку в 148 кг. Если колонна у нас сечением 300х300 мм, то ее площадь равна 30∙30 = 900 см2, и такая колонна может выдержать 148∙900 = 133200 кг = 133,2 т вертикальной силы. Число внушает уважение. Но это лишь при условии строго вертикальной нагрузки, расположенной четко по оси колонны (в геометрическом центре сечения). В реальности картина обычно далека от идеала, и даже в запроектированной с центральной нагрузкой колонне может произойти смещение этой нагрузки в любую сторону на какую-то случайную величину. Эту величину принято называть случайным эксцентриситетом. А если нагрузка приложена с эксцентриситетом, т.е. не посередине, то колонну будет гнуть в ту сторону, в которую смещена нагрузка. То есть, в колонне возникает изгибающий момент. А на изгиб железобетон работает гораздо хуже, чем на сжатие. И арматура, которая получается в результате расчета колонны, не мало увеличена именно за счет действия изгибающих моментов в колонне.

Какие бывают расчетные ситуации для колонн?

Ситуация А. Когда на колонну действует только вертикальная сила.

В этой ситуации можно выделить несколько случаев.

Случай 1. Вертикальная сила приложена четко по оси колонны (в геометрическом центре сечения).

Как на самом деле эта сила учитывается в расчете?

Помимо самой силы N в расчет еще включаются две величины: изгибающие моменты, которые могут возникнуть в результате смещения силы N в ту или иную сторону на величину случайного эксцентриситета. Да, этот эксцентриситет невелик, он определяется по конкретным формулам, но нагрузку на колонну он увеличивает.

В итоге вместо одной силы N мы получаем N + М1 + М2, и, конечно, это отразится на армировании.

Случай 2. Вертикальная сила, действующая на колонну сбита вдоль вертикальной оси, но находится на горизонтальной оси.

В этом случае вертикальная сила создает конкретный изгибающий момент М = N∙e1. Этот изгибающий момент вызывает в колонне определенные деформации – часть сечения колонны оказывается сжатой, а часть – растянутой.

При небольшом моменте и маленьком эксцентриситете растяжения может не возникнуть вообще, просто колонна будет сжата не равномерно – где-то больше, а где-то меньше.

Если в колонне есть растянутая зона, армирования следует ждать большого – бетон не работает на растяжение, все растягивающие усилия примет на себя арматура.

Еще хочется добавить, что если вертикальная сила сбита только в одном направлении, и эксцентриситет сбивки нам известен, то в перпендикулярном направлении при расчете нам может потребоваться задать случайный эксцентриситет, чтобы учесть неучтенные неблагоприятные факторы. В итоге на колонну в одном направлении будет действовать изгибающий момент М1, возникший из-за смещения силы N на расстояние e1 относительно оси колонны; а в другом направлении – изгибающий момент М2, возникший из-за возможного смещения силы N на величину случайного эксцентриситета еа.

Расчет такой колонны происходит в два этапа: сначала рассчитывается колонна в плоскости изгиба (N + М1), затем из плоскости изгиба (N + М2). По результатам каждого расчета находится площадь арматуры для двух противоположных граней колонны.

Потом эту арматуру нужно будет пересчитать в конкретные арматурные стержни и законструировать сечение колонны.

Примером для такого случая будет шарнирное опирание на колонну сборной балки (например, опирание на консоль). Балка никак не может передать нагрузку ровно по центру, эта нагрузка всегда будет смещена в сторону от оси колонны. Расстояние смещения и есть эксцентриситет е1. А вот случайный эксцентриситет еа для такого случая может быть вызван тем, что монтажники случайно установили балку не ровно по оси колонны, а со сбивкой на пару сантиметров в сторону. Бывает? Бывает. Вот всякие такие случайности и учитывает случайный эксцентриситет (простите за тавтологию).

Случай 3. Бывает, что сила N сбита относительно обеих осей (или же вертикальных сил две и более, и каждая из них сбита в какую-то сторону). Тогда и М1, и М2 определяются умножением соответствующей силы N на соответствующий эксцентриситет – расстояние от оси колонны до точки приложения нагрузки.

Этот случай самый сложный. Он дает значительный изгиб колонны сразу в двух направлениях. И если в случае 2 сжатая зона колонны находилась у одной грани, а растянутая – у противоположной, то в случае 3 грань между сжатой и растянутой зоной проходит по косой, и максимально растянутым выходит один угол колонны, а максимально сжатым – противоположный. То есть, растянутыми будут две соседние грани колонны, а сжатыми – две противоположные им соседние грани.

Такая колонна рассчитывается на косое внецентренное сжатие. Армируется она, в итоге, симметрично, но самое главное – сделать расчет правильно, чтобы самые перенапряженные растяжением стержни выдержали.

Обычно расчет (ручной) на косое внецентренное сжатие производится в виде проверки: сначала задается армирование конкретными стержнями с конкретной привязкой, а затем выполняется проверочный расчет, определяющий, выдержит ли арматура нагрузку.

Если вы хотите глубже понять воздействие вертикальной силы и изгибающего момента на арматуру колонны, можете еще ознакомиться со статьей «Как армирование колонны зависит от нагрузки».

А мы продолжим рассматривать расчетные ситуации для колонн.

Ситуация Б. На колонну действует вертикальная сила N и один или более изгибающий момент М.

В рамах это очень распространенная ситуация. Ведь жестко соединенное с колонной перекрытие передает изгибающие моменты на колонну, и при расчете рамы мы все эти моменты определяем как нагрузку на нашу колонну.

В данной ситуации мы можем выделить два случая.

Случай 1. Когда изгибающий момент (или сумма всех изгибающих моментов) приложен к колонне в одной плоскости.

Такая колонна рассчитывается как внецентренно сжатая. По сути, нагрузка на нее подобна нагрузке по случаю 2 ситуации А, только к моменту от силы N прибавляется еще и момент от перекрытия. Из плоскости колонны также действует момент от силы N, приложенной со случайным эксцентриситетом.

Случай 2. Когда изгибающие моменты (или сумма моментов) действуют на колонну в двух плоскостях.

Эта компоновка сил подобна случаю 3 ситуации А, расчет колонны ведется на косое внецентренное сжатие.

В чем особенность наличия изгибающих моментов в колонне (то ли от сбитой от центра вертикальной силы, то ли непосредственно моментов от перекрытия)? Как я уже писала выше, моменты вызывают изгиб колонны, а изгиб может привести к возникновению растяжения в части сечения колонны. И как только появляется растяжение, сразу сильно возрастает армирование. Что можно сделать в ситуациях с перегруженными изгибающим моментом колоннами, вы можете узнать из статьи «Изгибающие моменты в колонне. Что можно сделать?»

Источник