Каким способом пользуются при доказательстве третьего признака равенства треугольников

Признаки равенства треугольников

О чем эта статья:

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

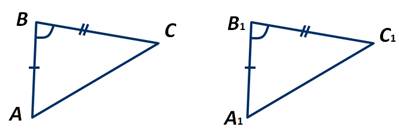
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

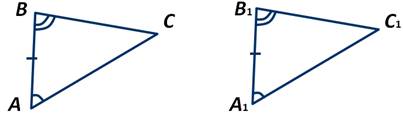
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

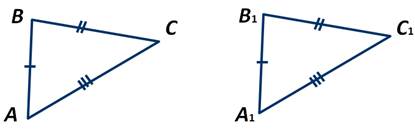
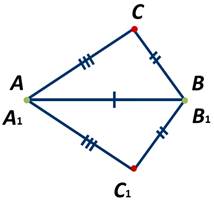
Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

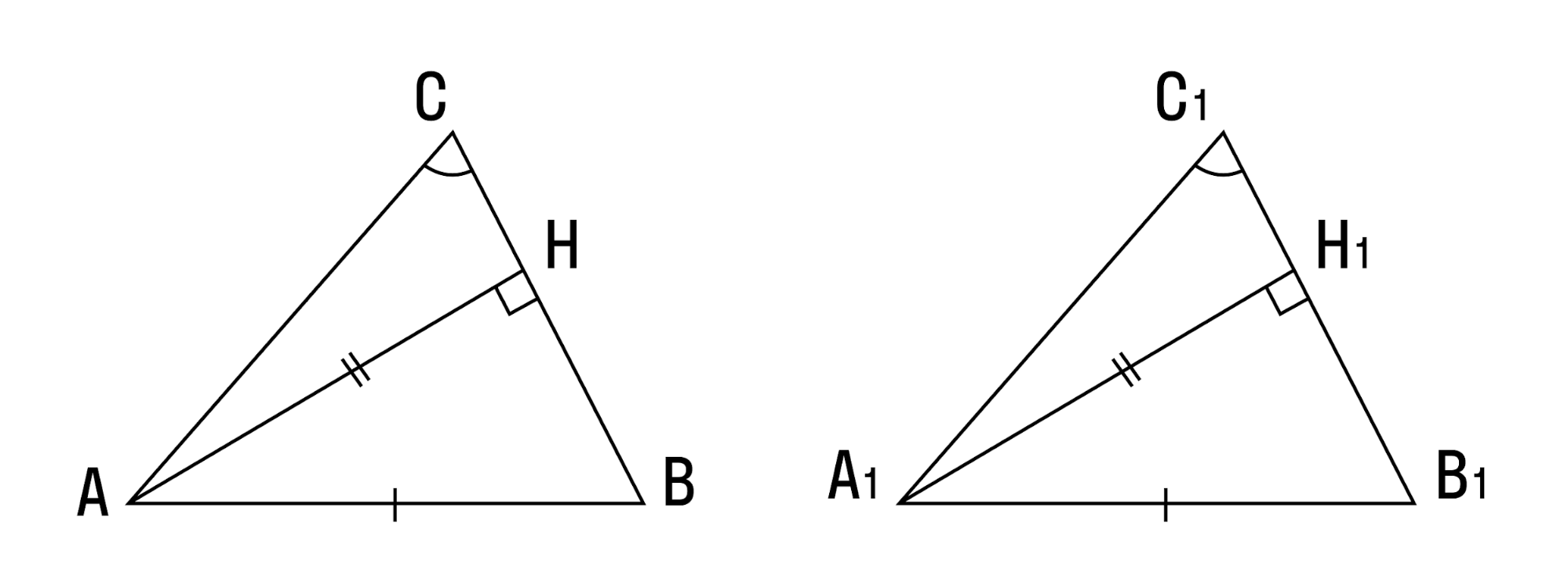
1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
   
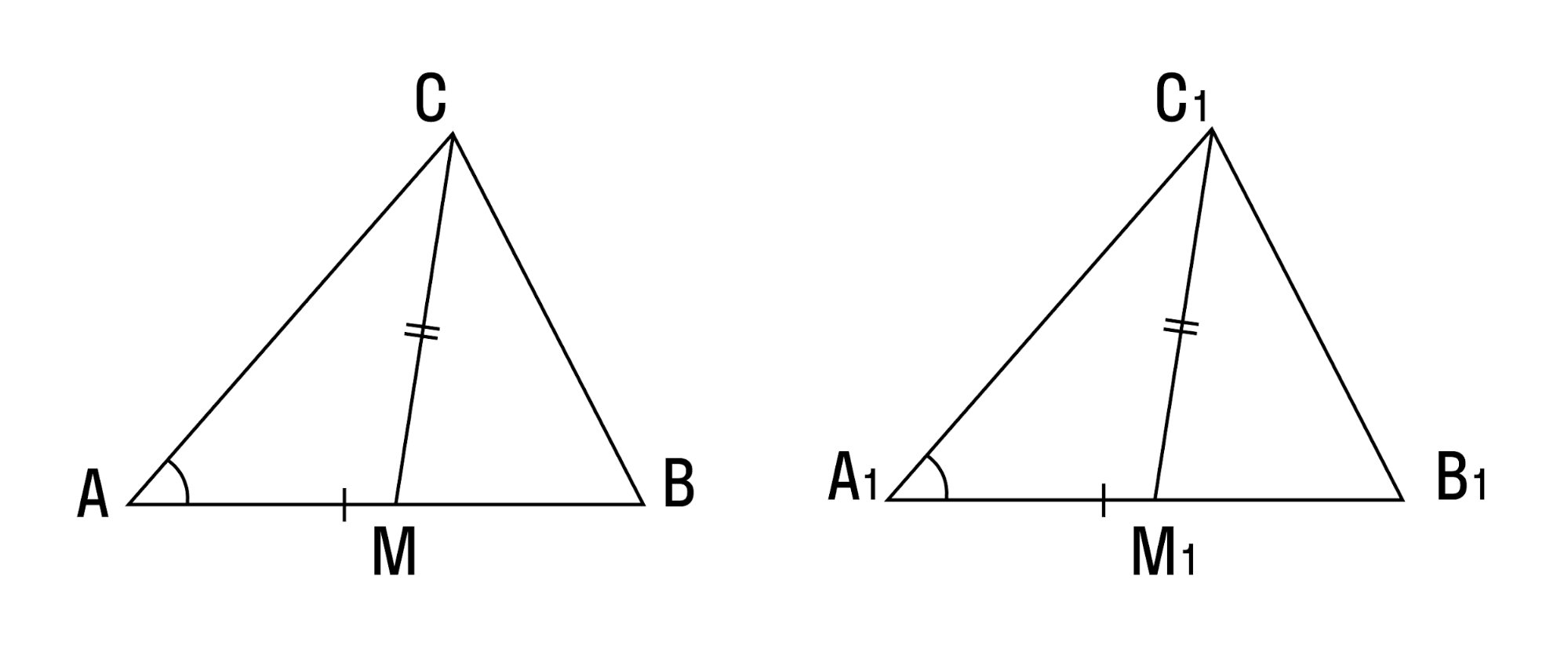
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
   
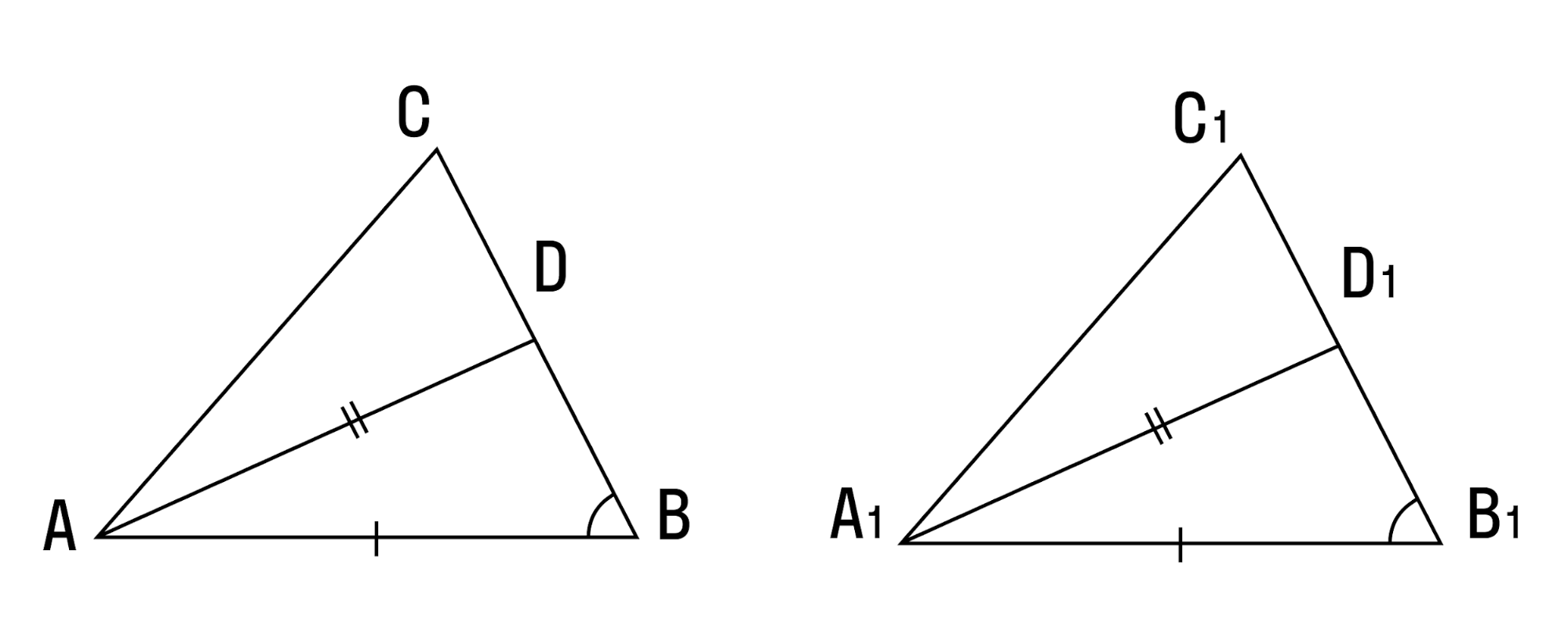
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
   
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
   
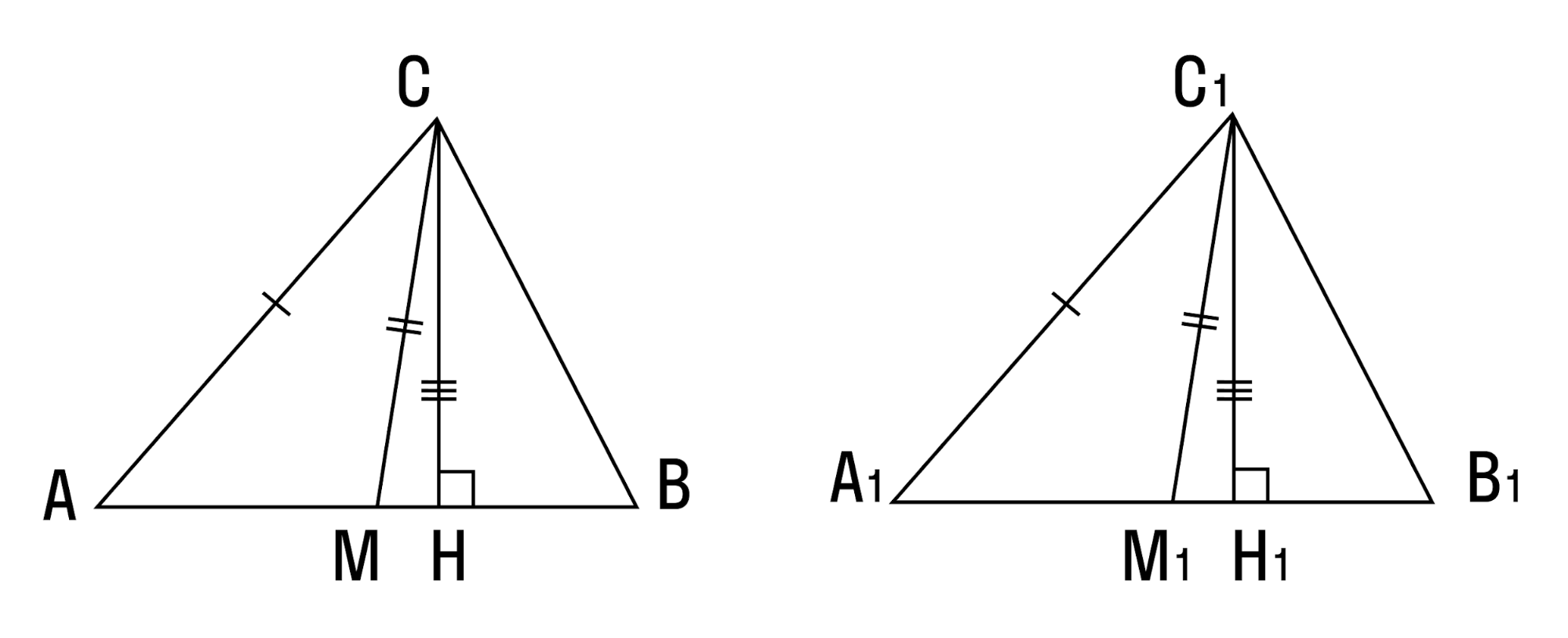
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
   

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Источник

3 признак равенства треугольников

(Третий признак равенства треугольников — по трём сторонам)

Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Дано:

Приложим треугольник A₁B₁C₁ к треугольнику ABC так, чтобы

• вершина A₁ совместилась с вершиной A,
• вершина B₁ совместилась с вершиной B,
• точки C₁ и C лежали по разные стороны от прямой AB.

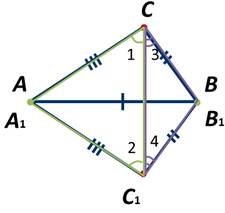
При этом возможны три случая взаимного расположения луча CC₁ и угла ACB.

I. Луч CC₁ проходит внутри угла ACB.

Проведём отрезок CC₁.

По условию AC=A₁C₁ и BC=B₁C₁, поэтому треугольники ACC₁ и BCC₁ — равнобедренные с основанием CC₁.

Если к равным углам прибывать равные углы, то получим равные углы:

Таким образом, ∠ACB=∠AC₁B.

Точки A₁ и A, B₁ и B совмещены, то есть ∠AC₁B и ∠A₁C₁B₁ — один и тот же угол.

Для треугольников ABC и A₁B₁C₁ имеем:

Следовательно, ΔABC= ΔA₁B₁C₁ (по 1 признаку равенства треугольников).

II. Луч CC₁ проходит внутри угла ACB.

Так как AC=A₁C₁ и BC=B₁C₁, треугольники ACC₁ и BCC₁ — равнобедренные с основанием CC₁ и ∠ACC₁=∠AC₁C и ∠BCC₁=∠BC₁C (как углы при основании).

Если из равных углов вычесть равные углы, то получим равные углы:

III. Луч CC₁ совпадает со стороной угла ACB.

По условию BC=B₁C₁, поэтому треугольник BCC₁ — равнобедренный с основанием CC₁.

Отсюда ∠C₁=∠C (как углы при основании) и ΔABC= ΔA₁B₁C₁ (по 1 признаку равенства треугольников).

Источник

Третий признак равенства треугольников

Урок 11. Геометрия 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Третий признак равенства треугольников»

Вспомним первый и второй признаки равенства треугольников.

Первый признак равенства треугольников:

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников:

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Сформулируем третий признак равенства треугольников:

Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

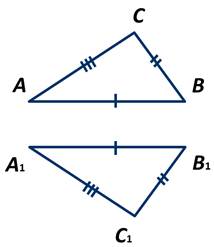
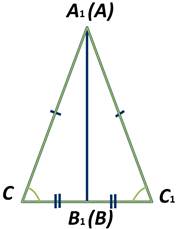
Приложим ∆ АВС к ∆ А₁В₁С₁ таким образом, чтобы вершина А совместилась с вершиной А₁, вершина В — с вершиной В₁, а вершины С и С₁ оказались по разные стороны от прямой А₁В₁.

Возможны три случая.

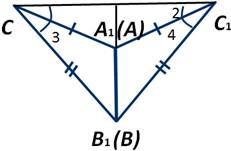
Рассмотрим первый случай. Так как по условию теоремы АС=А₁С₁, ВС=В₁С₁, то треугольники А₁С₁С и В₁С₁С являются равнобедренными. По теореме о свойстве углов равнобедренного треугольника угол 1 равняется углу 2, а угол 3 равняется углу 4. Поэтому ∠А₁СВ₁=∠А₁С₁В₁.

Получаем, АС=А₁С₁, ВС=В₁С₁ и ∠С=∠С1. Следовательно, ∆ АВС= ∆ А₁В₁С₁ по первому признаку равенства треугольников.

Рассмотрим второй случай. Так как по условию теоремы АС=А₁С₁, то ∆ СА₁С₁ является равнобедренным. По теореме о свойстве углов равнобедренного треугольника углы при основании С и С₁ равны. Можем сказать, что треугольники АВС и А₁В₁С₁ равны по первому признаку равенства треугольников, так как АС=А₁С₁ и ВС=В₁С₁ по условию теоремы, а ∠С=∠С₁.

И третий случай. По условию теоремы АС=А₁С₁ и ВС=В₁С₁. Из этого следует, что треугольники СА₁С₁ и СВ₁С₁ являются равнобедренными. Тогда по теореме о свойстве углов при основании равнобедренного треугольника ∠1=∠2 и ∠3=∠4. А следовательно, ∠С=∠С₁. Итак, треугольники АВС и А₁В₁С₁ равны по первому признаку равенства треугольников, так как АС=А₁С₁ и ВС=В₁С₁ по условию теоремы, а ∠С=∠С1.

Отрезок АС — общее основание равнобедренных треугольников АВС и АDC. Доказать, что треугольники BAD и BCD равны.

Рассмотрим ∆ BAD и ∆ BCD. У этих треугольников сторона АВ=ВС, сторона АD=DC, а сторона BD — общая.

Получаем, что треугольники BAD и BCD равны по третьему признаку равенства треугольников. Что и требовалось доказать.

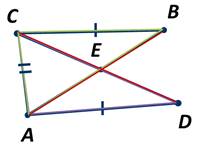
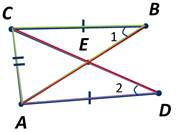
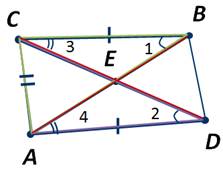
Два равных отрезка АВ и CD пересекаются в точке Е так, что расстояния AD и СВ равны. Докажите, что АЕ=СЕ.

Соединим точки А и С. И рассмотрим ∆ АВС и ∆ САD. У них сторона АС — общая, АВ=CD по условию, АD=СВ также по условию задачи. Тогда треугольники АВС и САD равны по третьему признаку.

Из равенства треугольников следует, что ∠1=∠2.

Соединив точки В и D аналогично можем доказать, что треугольники СВD и АDB равны, а следовательно, равны и углы 3 и 4.

Тогда можно утверждать, что ∆ СЕВ=∆ АЕD по второму признаку, так как у них ∠1=∠2, ∠3=∠4, а стороны АD и СВ равны по условию задачи. А следовательно, получаем, что сторона АЕ=СЕ. Что и требовалось доказать.

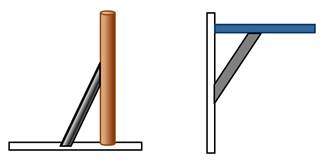
Рассмотрим свойство треугольника, которое следует из третьего признака равенства треугольников:

Возьмём две рейки, у которых два конца скреплены. Если будем сдвигать и раздвигать свободные концы этих реек, то угол между ними будет изменяться. А вот если мы возьмём третью рейку и скрепим её концы со свободными концами первых двух реек, то у нас уже не получится сдвинуть или раздвинуть никакие две стороны, а значит, нельзя изменить ни один угол.

Так как треугольник обладает таким свойством, то его называют жёсткой фигурой.

Это свойство треугольника делает его незаменимым в технике и строительстве. Элементы конструкции в форме треугольника сохраняют свою форму.

Например, чтобы закрепить столб в вертикальном положении к нему ставят подпорку. По такому же принципу устанавливается кронштейн.

А также стойки стремянки могут свободно раздвигаться, если не будут зафиксированы перемычкой.

Источник