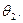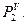Каким способом надо определять линию пересечения

Построение линии пересечения плоскостей, заданных различными способами

Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.

Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L₁ и L₂, принадлежащих линии пересечения.

1. Вводим вспомогательную горизонтальную плоскость γ₁. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1»C» и 2»3», совпадают с фронтальным следом пл. γ₁. Он обозначен на рисунке как f_0γ1 и расположен параллельно оси x.
2. Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
3. Находим горизонтальную проекцию точки L₁ на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L₁ лежит на фронтальном следе плоскости γ.
4. Вводим вспомогательную горизонтальную плоскость γ₂. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L₂.
5. Через L₁ и L₂ проводим искомую прямую l.

Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.

Пересечение плоскостей, заданных следами

Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П₁ и П₂.

1. Находим точку L’₁, расположенную на пересечении горизонтальных следов h_0α и h_0β. Точка L»₁ лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’₁.
2. Находим точку L»₂ на пересечении фронтальных следов пл. α и β. Точка L’₂ лежит на оси x. Её положение определяется по линии связи, проведенной из L»₂.
3. Проводим прямые l’ и l» через соответствующие проекции точек L₁ и L₂, как это показано на рисунке.

Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.

Пересечение плоскостей треугольников

Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

1. Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f_0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3»=A»B»∩f_0σ и 5»=A»С»∩f_0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
2. Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N» расположена на фронтальном следе f_0σ на одной линии связи с N’.

Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f_0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.

Через N и K проводим искомую прямую NK – линию пересечения ΔABC и ΔDEF.

Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₂. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π₂. С противоположной стороны от линии N»K» видимость треугольников меняется.

Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₁. Так как (∙)6» находится выше, чем (∙)7», то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π₁. С противоположной стороны от линии N’K’ видимость треугольников меняется.

Источник

Линия пересечения поверхностей

Линией пересечения поверхностей является линия, одновременно принадлежащая обеим пересекающимся поверхностям. Для построения точек линии пересечения используем метод вспомогательных секущих плоскостей.

Пусть даны две пересекающиеся поверхности и (рис. 40).

1. Проводим вспомогательную секущую плоскость S так, чтобы она пересекала обе данные поверхности.

2. Находим линии n и m пересечения плоскости S с поверхностями и

3. Определяем точки А и В взаимного пересечения линий n и m, лежащих в плоскости S.

Рис. 40. Пересечение поверхностей

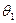
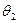
Точки А и В одновременно принадлежат поверхности и и, следовательно, являются точками искомой линии пересечения двух поверхностей. Проведя ряд вспомогательных секущих плоскостей, получим ряд точек, аналогичных точкам А и В. Линия, последовательно соединяющая эти точки, будет искомой линией пересечения двух поверхностей. Методом секущих плоскостей решаются задачи 4 и 6.

Дано: многогранник и поверхность вращения. С помощью вспомогательно-секущих плоскостей построить линию пересечения многогранной и поверхности вращения, выделив ее видимые и невидимые участки (пример на рис. 41, 42).

Указания к задаче 4

По табл. 4 определяется номер рисунка (см. приложение к табл. 4), на котором представлены две поверхности: одна – вращения, другая – многогранник (см. табл. 4). Количество граней n многогранника также указано в таблице, дано смещение Х от центра одной из поверхностей. Длину или высоту второй поверхности студент выбирает самостоятельно. Задачу решают в трех проекциях.

Намечают расположение вспомогательных секущих плоскостей частного положения (уровня) и с их помощью определяют характерные и промежуточные точки линии пересечения поверхностей. Плоскости следует выбирать так, чтобы линии их пересечения с поверхностями проецировались в простейшие фигуры (окружности или прямые).

№ вар.	Рисунок	n граней	х	№ вар.	Рисунок	n граней	х
—
—	—
—
—	—
—
—
Продолжение таблицы 4
—	—
—
—
—	—
—	—
—	—
—
—	—
—
—	—
—
—
—

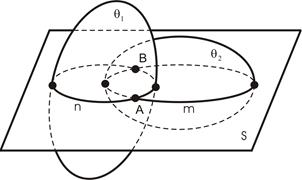
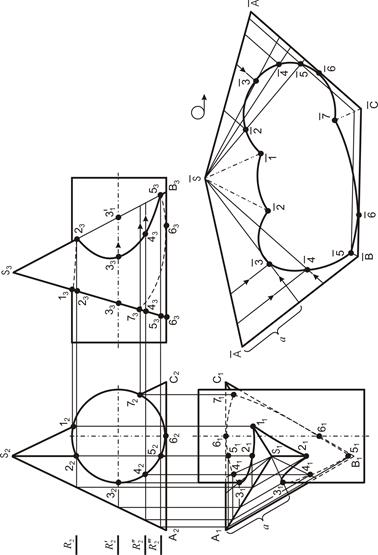
На примере решения задачи 4 (см. рис. 41) представлены сфера и проецирующая призма АВСD, следовательно, на фронтальной проекции линия пересечения уже определена. Вспомогательные плоскости в данном случае горизонтальные, они пересекают сферу по окружностям, а призму – по прямоугольникам. Точками пересечения поверхностей являются точки пересечения контуров фигур сечения поверхностей, лежащих в одной и той же вспомогательно-секущей плоскости. Каждая секущая плоскость может определить от одной до четырех точек линии пересечения в зависимости от характера пересекающихся поверхностей, их расположения относительно друг друга и положения секущей плоскости. Для гранной поверхности необходимо определить точки пересечения, принадлежащие ребрам, а для поверхности вращения – очерковым образующим.

На чертеже сфера представлена своим очерком на фронтальной и профильной проекции окружности главного меридиана, а на горизонтальной проекции – экватором.

Рис. 41. Сфера и призма

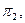
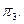
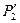
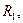
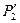
Точки 1 и 7 принадлежат главному меридиану на плоскости а точки 4 и 6 – на плоскости Точки 2 и 5 лежат на экваторе (2₁ и 5₁). Все остальные точки лежат на параллелях. По грани призмы ВС проводим первую горизонтальную плоскость – она пересекает сферу по окружности а призму – по грани ВС. На горизонтальной проекции определяют точки В₁ и С₁. Для нахождения остальных точек поступают так же, проводя плоскости до

Построить развертку многогранной поверхности и нанести на ней линию пересечения (заданная поверхность задачи 4).

Указания к задаче 5

Определяют натуральную величину одного из ребер многогранника и строят одну грань, затем последовательно к ней пристраивают остальные грани. Линия пересечения поверхностей наносится на развертку с помощью характерных точек.

На рис. 41 представлена развертка прямой призмы, у которой натуральная величина ребра – горизонтальные проекции, натуральная величина основания – фронтальная проекция.

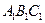
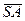
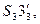
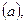
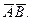
На рис. 42 представлено пересечение трехгранной пирамиды и цилиндра. При решении задачи используют горизонтальные плоскости, которые пересекают пирамиду по треугольникам, подобным основанию, а цилиндр – по прямоугольникам. На рис. 42 натуральная величина ребра у трехгранной пирамиды – это профильная прямая S₃B₃. Горизонтальная проекция основания – это натуральная величина. По чертежу на ребре откладывается действительная величина проводится линия, параллельная основанию. На горизонтальной проекции пирамиды проводим дополнительную прямую через точку 3₁ до встречи с основанием и затем эту величину переносим на Точка пересечения двух прямых определяет положение точки на развертке.

Рис. 42. Пирамида и цилиндр

Даны две пересекающиеся поверхности вращения. Способом вспомогательно-секущих плоскостей построить линию их пересечения, выделив ее видимые и невидимые участки (пример решения задачи на рис. 43).

Указания к задаче 6

По табл. 5 определяется номер рисунка (см. приложение к табл. 5), на котором представлены две поверхности вращения и заданы координаты центра расположения осей одной из поверхностей. Чертежи выполняются по размерам, представленным в таблице, где d₁ и d₂ – диаметры пересекающихся поверхностей, h – высота одной из поверхностей (если высота или длина второй поверхности не указаны, студент принимает ее самостоятельно), X, Y, Z – смещения от центра одной из поверхностей.

№ вар.	№ рис.	d1	d2	h	x	y	z	№ вар.	№ рис.	d1	d2	h	x	y	z
-15	—	—	—
—	—	-30	—
—	—	—	-10	—	—
—	-30	—
—	—	—	-15	—
—	—	—	—
—	—	—	—	—	—	—
—	—	—	—	—	—
—	—	—
—	—	—	—	-10	—
-20	—	-20	—	—
Продолжение таблицы 5
—	—	—	—
—	—	—	—	—	—
—	-10	—	—	—	—	—
—	-10	—	-20	—
—	—	—	—	—	—
—	—	—
—	—	—	—
—	-10	—	—	-20	—
-25	—	-25	—	—
—	—	—	—
—	—
—	—	—
—	—	—	—	—	—
-15	—	—	—	—

На рис. 43 дан пример решения задачи 6 – пересечение поверхностей вращения (в нашем случае усеченный конус и цилиндр). Цилиндр на фронтальной плоскости проекций проецируется действительной величиной основания. Наиболее рациональный метод решения этой задачи – метод секущих плоскостей. На фронтальной проекции цилиндра выбираем характерные точки (точки, лежащие на очерковых образующих): А, С, Е принадлежат очерковым образующим конуса, а точки N, B, D и M – образующим цилиндра. Чтобы получить более точно линию пересечения поверхностей, выбираем случайные точки 1, 2, 3 и 4.

Для нахождения горизонтальных проекций этих точек применяют горизонтальные плоскости Р. Усеченный конус пересекается этими плоскостями по окружности радиусом, равным расстоянию от оси вращения до очерковой образующей, а цилиндр – по прямоугольникам. Соединив последовательно эти точки, получим плавную линию пересечения.

Источник