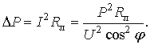Повышение коэффициента мощности в цепях синусоидального тока

Большинство современных потребителей электрической энергии имеют индуктивный характер нагрузки, токи которой отстают по фазе от напряжения источника. Так для асинхронных двигателей, трансформаторов, сварочных аппаратов и других реактивный ток необходим для создания вращающегося магнитного поля у электрических машин и переменного магнитного потока трансформаторов.

Активная мощность таких потребителей при заданных значениях тока и напряжения зависит от cos φ:

P = UICosφ , I = P / UCosφ

Снижение коэффициента мощности приводит к увеличению тока.

Косинус фи особенно сильно снижается при работе двигателей и трансформаторов вхолостую или при большой недогрузке. Если в сети есть реактивный ток мощность генератора, трансформаторных подстанции и сетей используется не полностью. С уменьшением cos φ значительно возрастают потери энергии на нагрев проводов и катушек электрических аппаратов.

Например, если активная мощность остается постоянной, обеспечивается током 100 А при cos φ =1, то при понижении cos φ до 0,8 и той же мощности сила тока в сети возрастает в 1,25 раза ( I а = I сети х cos φ , I с = I а / cos φ ).

Потери на нагрев проводов сети и обмоток генератора (трансформатора) Pнагр = I 2 сети х Rсети пропорциональны квадрату тока, то есть они возрастают в 1,25 2 = 1,56 раза.

При cos φ = 0,5 сила тока в сети при той же активной мощности равна 100 / 0,5 = 200 А, а потери в сети возрастают в 4 раза (!). Возрастают потери напряжения в сети, что нарушает нормальную работу других потребителей.

Счетчик потребителя во всех случаях отсчитывает одно и то же количество потребляемой активной энергии в единицу времени, но в последнем случае генератор подает в сеть силу тока, в 2 раза большую, чем в первом. Нагрузка же генератора (тепловой режим) определяется не активной мощностью потребителей, а полной мощностью в киловольт-амперах, то есть произведением напряжения на силу тока, протекающего по обмоткам.

Если обозначить сопротивление проводов линии R л, то потери мощности в ней можно определить так:

Таким образом, чем выше потребителя, тем меньше потери мощности в линии и дешевле передача электроэнергии.

Коэффициент мощности показывает, как используется номинальная мощность источника. Так, для питания приемника 1000 кВт при φ = 0,5 мощность генератора должна быть S = P / cos φ = 1000 / 0 ,5 = 2000 кВА, а при cosφ = 1 S = 1000 кВА.

Следовательно, повышение коэффициента мощности увеличивает степень использования мощности генераторов.

Для повышения коэффициента мощности (cos φ ) электрических установок применяют компенсацию реактивной мощности .

Увеличения коэффициента мощности (уменьшения угла φ — сдвига фаз тока и напряжения) можно добиться следующими способами:

1) заменой мало загруженных двигателей двигателями меньшей мощности,

2) понижением напряжения

3) выключением двигателей и трансформаторов, работающих на холостом ходу,

4) включением в сеть специальных компенсирующих устройств, являющихся генераторами опережающего (емкостного) тока.

На мощных районных подстанциях для этой цели специально устанавливают синхронные компенсаторы — синхронные перевозбужденные электродвигатели.

Чтобы повысить экономичность энергетических установок наиболее часто используют батареи конденсаторов , подключаемые параллельно индуктивной нагрузке (рис. 2 а).

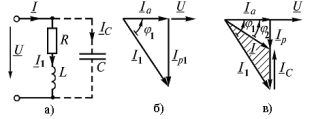
Рис. 2 Включение конденсаторов для компенсации реактивной мощности: а — схема, б, в — векторные диаграммы

Для компенсации cos φ в электрических установках до нескольких сотен кВА применяют косинусные конденсаторы. Их выпускают на напряжение от 0,22 до 10 кВ.

Емкость конденсатора, необходимую для повышения cosφ от существующего значения cosφ 1 до требуемого cosφ 2 , можно определить по диаграмме (рис. 2 б, в).

При построении векторной диаграммы в качестве исходного вектора принят вектор напряжения источника. Если нагрузка представляет собой индуктивный характер, то вектор тока I 1 отстает от вектора напряжения на угол φ 1 I а совпадает по направлению с напряжением, реактивная составляющая тока I р отстает от него на 90° (рис. 2 б).

После подключения к потребителю батареи конденсаторов ток I определяется как геометрическая сумма векторов I 1 и I c . При этом вектор емкостного тока опережает вектор напряжения на 90° (рис. 2, в). Из векторной диаграммы видно, что φ 2 1 , т.е. после включения конденсатора коэффициент мощности повышается от cos φ1 до cos φ2

Емкость конденсатора можно рассчитать при помощи векторной диаграммы токов (рис. 2 в) Ic = I р1 — I р = I а tg φ1 — I а tg φ 2 = ωCU

Учитывая, что P = UI а , запишем емкость конденсатора С = (I а / ωU ) х ( tg φ1 — tg φ 2 ) = (P / ωU 2 ) х ( tg φ1 — tg φ2 ) .

На практике обычно коэффициент мощности повышают не до 1,0, а до 0,90 — 0,95, так как полная компенсация требует дополнительной установки конденсаторов, что часто экономически не оправдано.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Способы повышения КПД и коэффициента мощности АЭП

ГОСТР 51541-99. Энергосбережение. Энергетическая эффективность. Состав показателей.

ГОСТР 51387—99. Энергосбережение. Нормативно-методическое обеспечение.

Общие вопросы энергосбережения

Энергосбережение в регулируемом АЭП

Снижение потерь энергии в переходных режимах

Способы повышения КПД и коэффициента мощности АЭП

Общие вопросы энергосбережения

Вопросы

Энергосбережение в АЭП

Лекция 15

Энергосбережение — это комплекс правовых, технических и экономических мер, направленных на эффективное использование энергетических ресурсов. В соответствии с Федеральным законом РФ «Об энергосбережении» на промышленном предприятии должны быть разработаны мероприятия по экономии электроэнергии применительно к каждой электроустановке. В первую очередь это относится к устройствам с электрическим приводом, основной элемент которого электродвигатель. Известно, что более половины всей производимой в мире электроэнергии потребляется электродвигателями в электроприводах рабочих машин, механизмов, транспортных средств. Поэтому меры по экономии электроэнергии в электроприводах наиболее актуальны.

Основные положения энергосбере­жения регламентированы государ-ственными стандартами РФ:

ГОСТ Р 51379—99. Энергосбережение. Энергетический паспорт промышленного потребителя топливно-энергетических ре­сурсов.

ГОСТ Р 31380—99. Энергосбережение. Методы подтверждения соответствия по­казателей энергетической эффективности энергопотребляющей продукции их нор­мативным значениям. Общие требования.

Задачи энергосбережения требуют оптимального решения не только в процессе эксплуатации электрических машин, но и при их проектировании.

При проектировании и эксплуатации разного рода электроприводов необходимо учитывать потребление и потери электроэнергии, влияние ЭП на сеть и другие электроприемники. Оценка этих свойств осуществляется с помощью так называемых энергетических показателей: коэффициента полезного действия, коэффициента мощности, потерь мощности и энергии.

С целью уменьшения потерь энергии в период пуска или торможения двигатели к рабочим машинам подбирают таким образом, чтобы приведенный момент инерции привода при одной и той же скорости был наименьшим. Это реализуется за счет применения малогабаритных двигателей, имеющих пониженный J (двигатели с повышенным отношением длинны якоря к его диаметру, с полым или дисковым якорем). Целесообразно использование двух двигателей половинной мощности. Расчеты показывают; что ∑J двух двигателей половинной мощности оказывается меньше момента инерции одного двигателя на полную мощность. Например, два двигателя типа 4АН200 мощностью по 45 кВт имеющий суммарный момент инерции 2·1,38=2,76 кг·м 2 . Двигатель 4АН250 мощностью 90 кВт на ту же скорость имеет j=3,53 кг·м 2 , т.е. почти на 30% больше.

Другой способ уменьшения потерь ЭП – регулирование скорости идеального холостого хода, что хорошо реализуется в ступенчатом пуске ЭП (для АД – регулирование частоты вращения с помощью частоты питающего тока или числа пар полюсов; для ДПТ – регулирование частоты вращения с помощью напряжения).

При ступенчатом пуске отмечается снижение потерь электрической энергии в 2 раза.

За счет изменения в переходном процессе w₀ снижаются потери энергии в роторе АД. Уменьшение потерь энергии в роторе вызовет и снижение потерь в статоре и полных потерь в АД. Приведенный момент инерции ЭП зависит не только от момента инерции двигателя или рабочей машины, но и от передачи отношения между ними. Для уменьшение потерь энергии при пуске, передаточное отношение – i следует выбирать исходя из получения минимального приведенного момента инерции ЭП и проверять экономическим расчетом.

КПД ЭП, как электромеханическая система определяется произведением преобразователя, управляющего устройства, электродвигателя и механической передачи η_эп=η_п·η_уу·η_эд·η_мп.

Наиболее значимой величиной является КПД двигателя, который растет с увеличением мощности и частоты вращения.

КПД зависит также от развиваемой им полезной механической мощности на валу (рис. 1).

Работа ЭП, как и любого другого потребителя характеризуется коэффициентом мощности

сos =.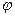

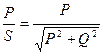
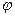
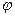
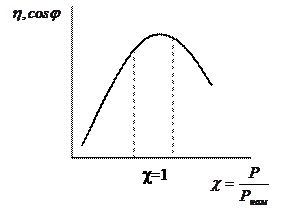Если Q не потребляется, то сos=1. Потребляя Q ЭП дополнительно загружает систему электроснабжения, вызывая дополнительные потери напряжения и энергии, поэтому cosдолжен стремится к единице. Достаточно часто, коэффициент мощности повышают компенсацией реактивной мощности статическими конденсаторами (в данном случае реактивная мощность для создания электромагнитного поля осуществляется от конденсаторов, расположенных непосредственно у АД).

Рисунок 1 – Зависимость КПД и коэффициента мощности электродвигателя от кратности нагрузки

Способы повышения КПД и коэффициента мощности ЭП:

— ограничение времени работы на холостом ходу;

— обеспечение нагрузки близкой к номинальной (в том числе путем замены малонагруженного (менее 40% от номинальной мощности) двигателя на двигатель меньшей мощности (должно быть экономически обоснованно));

Источник

Линия электропередачи постоянного тока

Если линия электропередачи имеет небольшую длину, при которой можно пренебречь утечкой тока через изоляцию, то ее электрическую схему можно представить в виде последовательного соединения сопротивления линии R_Л, равного суммарному сопротивлению прямого и обратного проводов, и сопротивления нагрузки R_Н (рис. 1.23).

При анализе работы линии нас интересуют, главным образом, три вопроса: напряжение на нагрузке, величина передаваемой мощности и коэффициент полезного действия передачи. Режимы работы линии удобно рассматривать в виде зависимостей различных величин от тока в линии, равного:

Падение напряжения в линии ΔU и напряжение на нагрузке U₂ определяются следующими выражениями:

Если U₁ и R_Л постоянны, то оба выражения представляют собой линейные функции тока (рис. 1.24). В режиме холостого хода (при I = 0) Δ U = 0, а U₂ = U₁. С ростом тока падение напряжения в линии возрастает, а напряжение на нагрузке уменьшается, и в режиме короткого замыкания (при R_Н = 0)

где, все входное напряжение гасится на сопротивлении линии.

Мощность на входе линии линейно зависит от тока: P₁ = U₁I. При холостом ходе она равна нулю, а при коротком замыкании вычисляется по формуле:

Потери мощности в линии представляют собой квадратичную функцию тока. Ее график – парабола, проходящая через начало координат. При I = 0: Δ P = 0; при I = I_K:

т.е. в режиме короткого замыкания мощность, поступающая в цепь, полностью теряется в линии.

Мощность, поступающая в нагрузку, равна разности мощности в начале линии и мощности, теряемой в проводах:

Последнее выражение представляет собой уравнение параболы со смещенной вершиной и с обращенными вниз ветвями, проходящими через точки I = 0 и I = I_K.

Мощность нагрузки представляет собой довольно сложную зависимость от сопротивления R_Н:

При RН = 0: Р 2 = 0; при возрастании RН мощность Р 2 сначала возрастает, достигает максимального значения и начинает убывать, стремясь к нулю при

R _Н → ∞ (рис. 1.25).

Выясним, при каком сопротивлении нагрузки передаваемая ей мощность максимальна. Для этого продифференцируем функцию (1.15) по R_Н и приравняем ее к нулю:

Приравняв к нулю числитель производной, получим:

То есть мощность, получаемая нагрузкой, максимальна, когда сопротивление нагрузки равно сопротивлению линии.

Ток, протекающий при этом по линии, равен: т.е. составляет половину тока короткого замыкания, а мощность в конце линии равна:

Эти же результаты можно получить, исследуя на экстремум зависимость мощности P₂ от тока I (1.14).

Коэффициент полезного действия равен отношению мощностей в начале и конце линии:

Он представляет собой линейную функцию тока. При холостом ходе, когда I = 0, он равен единице (нет передачи энергии – нет потерь). При коротком замыкании вся передаваемая мощность теряется в линии, и КПД равен нулю.

Возможны и другие формулы для определения КПД:

Из данной формулы следует, что коэффициент полезного действия передачи определяется отношением сопротивлений линии и нагрузки.

При их равенстве, когда нагрузке передается максимальная мощность, h = 0,5 = 50 %. Этот режим, при котором теряется половина передаваемой энергии, на практике, естественно, не пригоден. В реальных линиях при передаче больших мощностей КПД составляет примерно 0,94–0,97. При этом сопротивление нагрузки значительно больше сопротивления линии.

Для анализа режимов электропередачи полезной оказывается еще одна формула. Так как I = P 2 /U 2 , а

, то

То есть при одной и той же мощности нагрузки Р₂, потери Δ Р пропорциональны сопротивлению линии и обратно пропорциональны квадрату напряжения. Для увеличения коэффициента полезного действия передачи необходимо повышение напряжения и снижение электрического сопротивления проводов линии путем увеличения их сечения и применения материалов с меньшим удельным сопротивлением.

Пример 1.6. Линия электропередачи с проводами марки А-120 длиной l = 1000 км питает нагрузку мощностью Р₂ = 50 МВт. Каким должно быть напряжение в начале линии, чтобы КПД передачи был не ниже 90 %?

Р е ш е н и е. Сопротивление одного километра провода марки А-120 R₀ = 0,27 Ом/км. Суммарное сопротивление прямого и обратного проводов линии составляет R_Л = 2lR₀ = 540 Ом.

Принимая h = 0,9, из формулы (1.17) получаем:

Для выполнения условий задачи напряжение в начале линии должно быть не ниже 548 кВ.

Источник