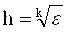Каким способом можно прогнозировать примерную величину шага для достижения заданной точности

Выбор шага интегрирования по заданной точности

Погрешность метода средних прямоугольников при вычислениях с постоянным шагом Dx оценивается величиной

,

где — вторая производная функции f(x).

Погрешность метода трапеций приблизительно равна

.

В общем случае погрешность формулы средних прямоугольников примерно вдвое меньше, чем у формулы трапеций. Поэтому, если значения функции одинаково легко определяются в любых точках, то лучше вести расчет по более точной формуле средних прямоугольников. Метод трапеций употребляют в тех случаях, когда функция задана только в узлах сетки, а в середине интервала ее значения неизвестны.

Главные члены погрешностей у формул средних прямоугольников и трапеций имеют различные знаки, поэтому, если вести расчеты по обеим формулам, точное значение интеграла будет, как правило, находиться в вилке между ними. Используя это свойство, можно добиться повышения точности расчетов. Так как

, ,

то, применяя комбинированную формулу

,

сократим основные источники погрешностей. Подставляя в нее конкретные значения, получим формулу

,

соответствующую методу Симпсона, погрешность которого оценивается величиной

.

В методах средних прямоугольников и трапеций уменьшение шага интегрирования Dx вдвое уменьшает погрешность оценки площади элементарного прямоугольника в 8 раз, однако, общее количество этих прямоугольников увеличивается в 2 раза, поэтому общая погрешность уменьшается приблизительно в 4 раза. Коэффициент уменьшения ошибки пропорционален величине второй производной и обычно не равен в точности 4, поскольку не является константой и сказывается также влияние членов более высокого порядка. Однако, при реальных вычислениях с функциями, имеющими непрерывные ограниченные вторые производные, можно ожидать, что удвоение числа элементарных отрезков для любой формулы – средних прямоугольников или трапеций – приблизительно учетверяет точность.

Если в методе Симпсона уменьшить шаг Dx в два раза, то каждое Dх 5 уменьшится в 32 раза, при этом общее количество элементарных фигур возрастет в 2 раза. Погрешность в целом уменьшится приблизительно в 16 раз.

При выборе количества разбиений n или величины шага Dx заранее неизвестно, какова будет погрешность вычисления интеграла. Кроме того, точное значение интеграла также неизвестно и сравнить полученное значение с точным нельзя.

Для оценки точности вычисления сравнивают два последовательных приближения к результату. Сначала задают некоторое начальное n₁, для которого вычисляют приближенное значение S₁. Затем число участков удваивают, n₁=2n₁, соответственно длины участков сокращаются вдвое, . Далее вычисляют новую сумму площадей более узких фигур S₂. Она точнее приближает искомое значение интеграла. Разность сравнивают с наперед заданным малым положительным числом e. При считают, что S₂ можно принять за приближенное значение интеграла, полученное с заданной точностью e. В противном случае процесс деления отрезков повторяют, принимая n₃=2n₂, вычисляют S₃ и сравнивают с e.

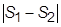
Для непрерывных функций условие должно наступить обязательно, если e>e_маш. Следует отметить, что выполнение условия в общем случае не означает, что погрешность вычисления интеграла меньше величины e. Здесь сравнивается окончательное значение S_k не с точным значением, а с вычисленным ранее при более крупном шаге интегрирования. Тем не менее, для многих функций такая оценка величины погрешности является достаточной.

При численном интегрировании величина погрешности зависит не только от используемого метода, но и от вида интегрируемой функции. Основным способом уменьшения погрешности вычисления интеграла является уменьшение ширины элементарного отрезка Dх, т.е. увеличение количества разбиений. Однако это приводит к увеличению объема вычислений и соответственно к увеличению продолжительности счета.

Вместе с тем влияние ширины отрезка Dх на точность расчета может быть неодинаковым на разных участках интегрирования. Если функция на некотором участке изменяется мало или ее вид близок к виду аппроксимирующей функции j(х), то для обеспечения требуемой точности целесообразно проводить вычисления с более крупным шагом. Там, где функция изменяется более быстро, целесообразно уменьшать шаг интегрирования.

Для обеспечения выбора приемлемого шага интегрирования на участке в зависимости от выбора типа метода интегрирования и поведения подинтегральной функции применяются адаптивные программы, построенные на алгоритмах с одной или двумя функциями, автоматически определяющими величину шага.

Пользователь подобной программы указывает конечный интервал [a,b] и допустимую погрешность e. Программа пытается вычислить величину S, такую, что

.

В процессе вычислений интервал [a,b] разбивается на подинтервалы [x_i-1,x_i]. В большинстве программ новый подинтервал получается делением пополам подинтервала, полученного на более раннем этапе вычисления. Реальное число подинтервалов и их длина зависят от функции f(x) и требуемой точности e.

Типичная схема применяет к подинтервалу две различные формулы. Например, схемы, основанные на формуле Симпсона, используют основную формулу с двумя элементарными отрезками

и составную формулу с четырьмя элементарными отрезками

.

Выражения S_1i и S_2i являются приближениями к величине интеграла

.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)

Источник

6.4. Выбор шага интегрирования

При вычислении значения определенного интеграла от функций, заданных аналитически, необходимо обеспечить требуемую точность расчета ε.

Точность вычисления можно повысить двумя способами:

1. Использовать более точную квадратурную формулу.

2. Увеличить количество узлов, соответственно уменьшить шаг интегрирования h.

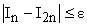
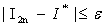
На практике обычно используется формула Симпсона, а требуемая точность расчета достигается вторым из указанных выше способов. Выполняется расчет с выбранным числом узлов n, затем выполняется расчет с удвоенным их числом. Если результаты отличаются более чем на требуемую точность, число узлов вновь удваивается. Расчет заканчивают, когда , полагая, что , т. е. последнее вычисленное приближенное значение интеграла отличается от точного значения не больше чем на заданную точность.

Такой способ называется Автоматическим выбором шага интегрирования и легко реализуется на ЭВМ.

Начальный шаг интегрирования рекомендуется выбирать из соотношения:

Где k = 1 для формул правых и левых прямоугольников;

k = 2 для формул трапеций и центральных прямоугольников;

k = 3 для формулы Симпсона.

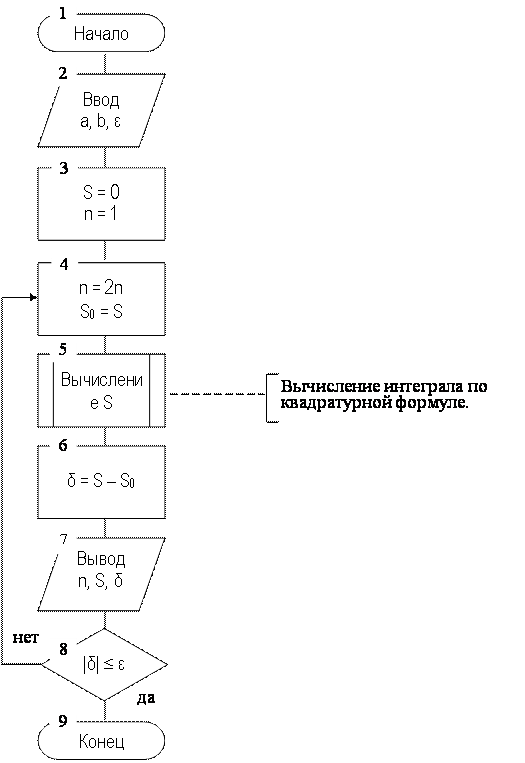Рис. 6.10. Схема алгоритма вычисления определенного интеграла

с автоматическим выбором шага интегрирования.

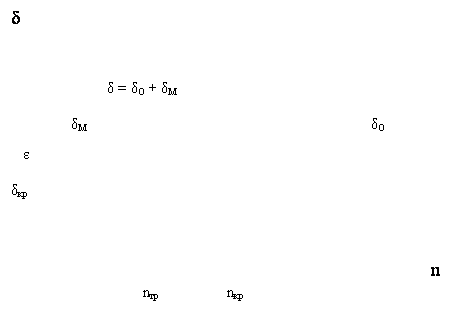
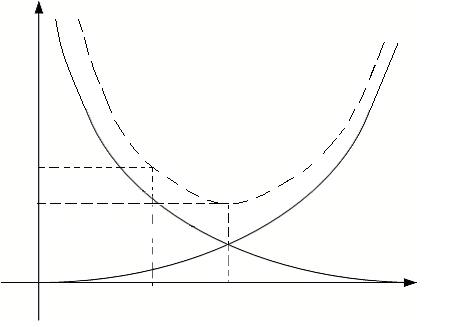
Важно напомнить, что погрешность решения включает погрешности метода δM и погрешность округления δO. При увеличении числа узлов n δM уменьшается, но растет δO, т. к. увеличивается количество арифметических действий для решения задачи. Зависимость этих величин показана на графике.

Рис. 6.11. Структура погрешности численного интегрирования.

Из графика следует, что требуемую точность ε следует выбирать больше δкр, иначе требуемая точность не может быть достигнута.

Источник

Автоматический выбор шага. Правило Рунге

При выполнении практических расчетов с применением рассмотренных квадратурных формул оценку погрешности получаемых результатов можно осуществлять априорно, используя соотношения (4.3.15) – (4.3.18), (4.3.21), (4.3.22), (4.3.25) и (4.3.26). Эти соотношения позволяют получить (для заданного шага h между узлами равномерной сетки h_x) оценку сверху для погрешности аппроксимации квадратурной формулы с точностью до максимума модуля производной того или иного порядка подынтегральной функции на отрезке интегрирования. С другой стороны, основываясь на этих соотношениях можно определить максимально возможное значение h, при котором удовлетворяются заданные требования к точности результатов расчета. Однако с практической точки зрения получить достоверную оценку максимума модуля производной, даже если известно аналитическое задание подынтегральной функции, достаточно сложно. Если аналитическое задание неизвестно (что чаще всего и имеет место), а функция представлена лишь табличными значениями, то задача получения такой оценки, как правило, становится практически неразрешимой. Таким образом, возникает необходимость применения других способов оценки погрешности численного интегрирования, один из которых основан на использовании правила Рунге.

В отличие от априорной (до того как будут произведены вычисления) оценки погрешности на основании соотношений (4.3.15) – (4.3.18), (4.3.21), (4.3.22), (4.3.25) и (4.3.26) для предлагаемого подхода имеет место апостериорная оценка, которая получается в результате анализа уже произведенных вычислений.

Пусть I_k – точное, а J_k ( h ) – приближенное значение определенного интеграла от функции f(x), полученное в результате расчета с шагом h по одной из рассмотренных ранее квадратурных формул на частичных отрезках разбиения [x_k, x_{k + 1}], k = 0, 1, 2, …, n – 1 отрезка [a, b]. Тогда будет справедливо приближенное равенство

где m – порядок точности используемой квадратурной формулы.

Напомним, что m = 2 для квадратурных формул левых (4.3.9) и правых (4.3.11) прямоугольников, m = 3 — для квадратурной формулы центральных (4.3.13) прямоугольников и квадратурной формулы (4.3.19) трапеций, m = 5 — для квадратурной формулы (4.3.23) Симпсона.

Уменьшим шаг сетки в два раза и повторим расчет по той же именно. квадратурной формуле. Обозначим результат расчета как J_k ( h /2) . Для него справедливо аналогичное (4.3.27) приближенное равенство

Из соотношений (4.3.27) и (4.3.28) имеем

(4.3.29)

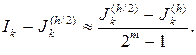
Полученное приближенное равенство часто называют правилом Рунге.

Пусть теперь задано достаточно малое число e > 0, определяющее требуемую точность вычисления значения определенного интеграла
от функции f(x) на отрезке [a, b] с помощью составной квадратурной формулы

(4.3.30)

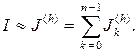
Здесь I – точное значение определенного интеграла на отрезке [a, b]; J ( h ) – приближенное значение этого интеграла, определенное с помощью составной квадратурной формулы.

Для каждого частичного отрезка разбиения [x_k, x_{k + 1}], k = 0, 1, 2, …, n – 1 дважды проведем вычисления по квадратурной формуле, имеющей порядок точности равный m, – с шагом h и h/2.

Согласно правилу Рунге (4.3.29) можно утверждать, что если
в результате для всех частичных отрезков разбиения будут выполняться неравенства

, (4.3.31)

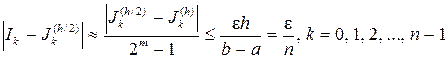
то очевидно, что для соответствующей составной квадратурной формулы требуемая точность будет обеспечена.

Если для некоторых частичных отрезков неравенство (4.3.31) не будет выполнено, то для них необходимо повторять расчет, уменьшая каждый раз шаг h сетки в два раза до тех пор, пока не будет обеспечено его выполнение.

Рассмотренная возможность выбора величины шага между узлами квадратурной формулы для обеспечения заданной точности вычисления лежит в основе процедур численного интегрирования с так называемым автоматическим выбором шага. Отметим, что такой способ определения шага позволяет в процессе численного интегрирования варьировать расстояние между узлами составной квадратурной формулы в области интегрирования. На участках, где интегрируемая функция f(x) медленно изменяет свои значения, шаг может оставаться достаточно большим, и лишь на участках наиболее быстрого изменения значений f(x) для обеспечения требуемой точности может потребоваться дробление шага.

Очевидно, что рассмотренная процедура автоматического выбора шага может быть реализована только в том случае, когда значения интегрируемой функции во вновь образующихся при дроблении шага узлах составной квадратурной формулы либо могут быть вычислены, либо уже заданы в имеющейся таблице ее значений.

Глава 5. Численные методы решения задачи Коши
для обыкновенных дифференциальных уравнений
и их систем

Источник