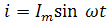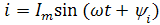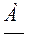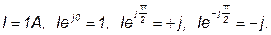Вопрос №3. Способы представления синусоидальных величин (10 мин.)
Синусоидальные величины могут быть представлены различными способами.
Примеры способов представления синусоидальных величин.
1. Тригонометрические функции (алгебраический)
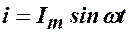
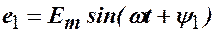
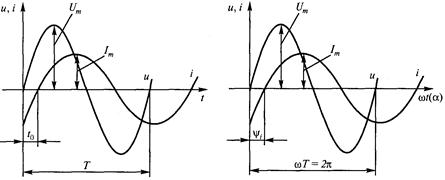
2. Временные диаграммы или графики изменения функции во времени (графический)
Характер изменения синусоидальных ЭДС, тока и напряжения с течением времени полностью определен формулами:
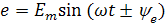
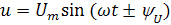
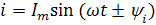
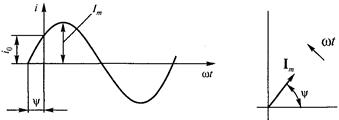
Недостаток формул – отсутствие наглядности. Для того, чтобы наглядно представить характер изменения исследуемой величины, принято изображать рассматриваемые зависимости графически в прямоугольной системе координат (рис. 11).
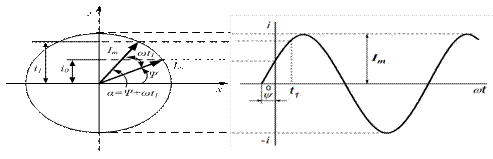
3. Вращающиеся вектора позволяют упростить действия над синусоидальными величинами по сравнению с двумя предыдущими методами (рис. 12).
Векторная диаграмма – совокупность нескольких векторов, соответствующих нулевому моменту времени. Необходимо иметь в виду, что на векторной диаграмме векторы изображают токи (напряжения) одинаковой частоты.
Вектор изображает синусоиду, если выполнены следующие условия:
· модуль вектора равен амплитудному значению синусоидальной величины (в масштабе);
· вектор наклонен к горизонтальной оси под углом, равным начальной фазе y;
· вектор вращается против часовой стрелки с угловой скоростью, равной угловой частоте тока;
· берутся проекции вектора на оси (рис. 13).
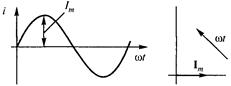
На рис. 14 показан вектор, изображающий синусоиду при начальной фазе, равной нулю (рис. 14).
На рис. 15 изображен вектор, изображающий синусоиду при начальной фазе y=π/4.
Ответьте на ряд вопросов.
Укажите выражение для тока, изображенного этими векторами.
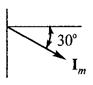 Im=2 А Im=2 А |  |
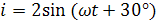 | |
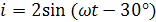 | |
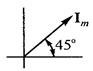 | 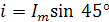 |
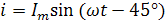 | |
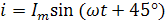 |
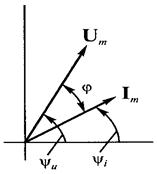
В практике расчета электрических цепей переменного тока начальная фаза часто не имеет существенного значения, но важен сдвиг по фазе между синусоидальными величинами. Этот сдвиг легко определить по векторной диаграмме. например, если в ветви протекает ток 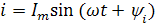
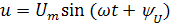
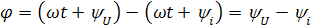
На рис. 17 изображены векторные диаграммы, также иллюстрирующие сдвиг фаз:
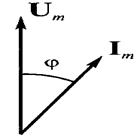
а – сдвиг фаз между током и напряжением φ=0;
б — сдвиг фаз между Е1 и Е2 φ=90°
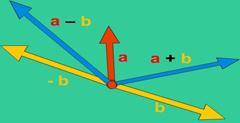
Вектора можно складывать и вычитать. При сложении векторов используют правило параллелограмма или переноса.
Вектора можно вычитать (рис. 20).
4. Комплексными числами. Вращающиеся векторы и изображаемые ими синусоидальные величины можно представить комплексными числами. Т.к. расположение векторов относительно друг друга на векторной диаграмме с течением времени не изменяется их можно изобразить в начальный момент времени на комплексной плоскости, т.е. представить комплексами (рис. 21):
в тригонометрической форме: 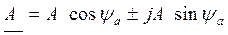
в показательной форме: 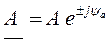
в алгебраической форме (см. рис. 11): 
где А – модуль комплекса 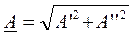
Yа=arctg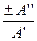
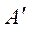
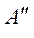
комплекса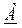
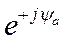
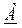
Вывод по третьему вопросу:синусоидальные токи и напряжения как функции времени могут быть описаны различными способами: алгебраически, векторными диаграммами и комплексами.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Способы изображения синусоидальных величин



1. Графическое изображение синусоидальных величин.
Для сравнения электрических величин, изменяющихся по синусоидальному закону, необходимо знать разность их начальных фаз. Если, например, на каком — либо участке ток 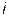
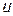
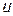
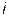
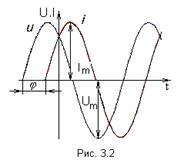 |
На рис. 3.2 для заданного элемента цепи представлены графики изменения во времени двух электрических величин: напряжения 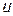
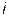
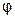
2. Векторное изображение синусоидальных величин.
При гармоническом изменении синусоидальной величины постоянной остаётся амплитуда. Этим можно воспользоваться для определения мгновенного значения электрической величины, не рассматривая графика её зависимости от времени.

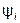
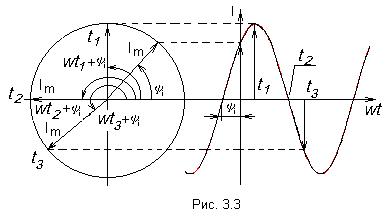 |
На рис. 3.3 показаны вращающийся вектор тока 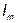
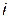

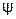
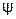
Если вращать вектор против часовой стрелки, то в любой момент времени он составит с горизонтальной осью угол, равный 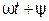
Совокупность векторов на плоскости, изображающих Э.Д.С., напряжения, токи одной частоты, называют векторной диаграммой.
При исследовании установившихся режимов векторы неподвижны, их длина равна действующим значениям электрических величин.
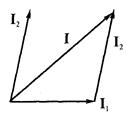
С помощью векторов можно производить геометрическое суммирование электрических величин.
Так, на рис. 3.4 показаны векторы токов 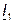
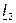
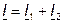

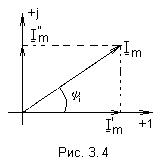 |
Векторные диаграммы широко используются при анализе электрических цепей переменного тока.
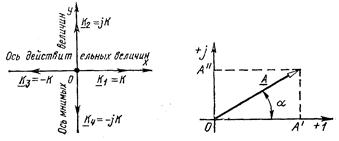
3. Представление синусоидальных величин комплексными числами.
Синусоидально изменяющуюся электрическую величину можно представить комплексным числом и изобразить в виде вектора на комплексной плоскости с прямоугольной системой координат.

На комплексной плоскости синусоидальная величина может изображаться в виде модуля и аргумента или в виде двух составляющих вектора, направленных по действительной и мнимой осям.
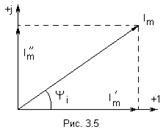
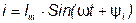
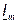
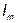
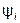
Составляющим вектора 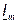

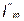
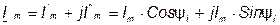
Вектор 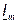
Обычно при расчётах пользуются действующими значениями.

При анализе электрических цепей переменного тока приходится иметь дело с умножением и делением электрических величин. В этом случае удобно пользоваться комплексами этих величин, записанными в показательной форме:
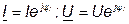
где 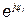
Например, при

Умножение на –j означает поворот вектора на угол –90 градусов (по часовой стрелке).
Источник