MT1102: Линейная алгебра (введение в математику)
Определение
Формулы алгебры высказываний %%X%% и %%Y%% называют равносильными (эквивалентными, тождественными), если при любых значениях переменных, входящих в эти формулы, значение истинности формул %%X%% и %%Y%% совпадают.
Пример
Пусть даны формулы $$ X = A \rightarrow B, Y = \overline \rightarrow \overline . $$
Построим таблицу истинности для этих двух формул
| %%A%% | %%B%% | %%X = A \rightarrow B%% | %%Y = \overline \rightarrow \overline%% |
|---|---|---|---|
| %%0%% | %%0%% | %%1%% | %%1%% |
| %%0%% | %%1%% | %%1%% | %%1%% |
| %%1%% | %%0%% | %%0%% | %%0%% |
| %%1%% | %%1%% | %%1%% | %%1%% |
Как видно из таблицы, истинностные значения данных формул совпадают при любых значениях %%A%% и %%B%%, следовательно, эти две формулы равносильны. Равносильность формул %%X%% и %%Y%% записывается в виде %%X \equiv Y%%.
Теоремы о равносильности формул
Теорема. Справедливы следующие равенства формул.
- Закон тождества $$ A \equiv A $$
- Закон коммутативности $$ \begin
A \land B \equiv B \land A \\ A \lor B \equiv B \lor A \end $$ - Закон ассоциативности $$ \begin
A \land (B \land C) \equiv (A \land B) \land C \\ A \lor (B \lor C) \equiv (A \lor B) \lor C \end $$ - Закон идемпотентности $$ \begin
A \land A \equiv A \\ A \lor A \equiv A \end $$ - Закон дистрибутивности $$ \begin
A \land (B \lor C) \equiv (A \land B) \lor (A \land C) \\ A \lor (B \land C) \equiv (A \lor B) \land (A \lor C) \end $$ - Законы де Моргана $$ \begin
\overline \equiv \overline \lor \overline \\ \overline \equiv \overline \land \overline \end $$ - Закон двойного отрицания $$ \overline<\overline> \equiv A $$
- Закон непротиворечия $$ A \land \overline \equiv 0 $$
- Закон исключения третьего $$ A \lor \overline \equiv 1 $$
- Тождества $$ \begin
A \land 1 \equiv A,
A \land 0 \equiv 0 \\ A \lor 0 \equiv A,
Где %%1%% — тождественно истиннная формула, а %%0%% — тождественно ложная формула.
Теорема дается без доказательства, так как эти формулы легко проверить, используя таблицы истинности.
Теорема. Для произвольной формулы существует равносильная ей формула, которая содержит только знаки отрицания и дизъюнкции.
Действительно, в произвольной формуле %%X%% могут присутствовать знаки конъюнкции, импликации и эквиваленции. Избавимся от этих знаков, заменяя подформулы, содержащие эти знаки, на равносильные им по следующим правилам:
- Заменяем %%A \leftrightarrow B%% на %%A \leftrightarrow B \equiv (A \rightarrow B) \land (B \rightarrow A)%%.
- Заменяем %%A \rightarrow B%% на %%\overline \lor B%%.
- Заменяем %%A \land B%% на %%\overline <\overline\lor \overline>%%.
Но использование только двух знаков очень неудобно, так как приводит к очень громоздким формулам, именно поэтому, обычно, используют три основных знака: отрицание, конъюнкция и дизъюнкция.
Обратная и противоположная теоремы
Пусть %%T%% некоторая теорема, имеющая вид $$ A \rightarrow B. $$
Назовем теорему %%T = A \rightarrow B%% прямой теоремой. Составим следующие высказывания:
Между этими теоремами есть следующие связи:
Источник
Каким способом можно определить равносильность формул логики
Равносильные формулы алгебры логики
Определение. Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).
Обозначение. A ≡ B .
.
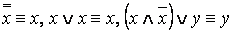
Определение. Формула A называется тождественно истинной (тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных (напр.,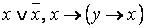 
).
Определение. Формула A называется тождественно ложной (противоречием), если она принимает значение 0 при всех значениях входящих в нее переменных (напр.,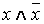 
).
Утверждение. Отношение равносильности рефлексивно, симметрично, транзитивно.
Связь между понятиями равносильности и эквивалентности: если формулы A и B равносильны, то формула A ↔ B тавтология, и обратно, если формула A ↔ B тавтология, то формулы A и B равносильны.
Равносильности алгебры логики можно разбить на 3 группы:
1. Основные равносильности.
· 
– законы идемпотентности;
· 
;
· 
;
· 
;
· 
;
· 
– закон противоречия;
· 
– закон исключенного третьего;
· 
– закон снятия двойного отрицания;
· 
– законы поглощения.
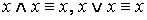
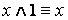
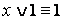
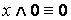
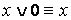
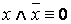
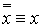
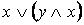
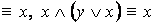
1. Равносильности, выражающие одни логические операции через другие:
· 
;
· 
;
· 
;
· 
;
· 
;
· 
.
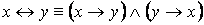
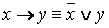
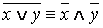
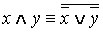
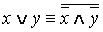
Замечание. Из равносильностей группы 2 следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание, или дизъюнкцию и отрицание. Дальнейшее исключение операций невозможно. Например, если использовать только конъюнкцию, то уже такая простая формула, как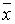 
не может быть выражена с помощью операции конъюнкции.
Существуют операции, с помощью которых может быть выражена любая из 5 логических операций:
1) Связка Шеффера – дизъюнкция отрицаний.
Обозначение. x | y ≡ (« x не совместно с y »).
Логические значения связки Шеффера описываются следующей таблицей истинности:
Имеют место следующие равносильности: а)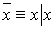 
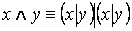
; б) 
.
2) Связка Лукасевича – конъюнкция отрицаний.
Обозначение . x ↓ y ≡ 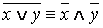(«ни x , ни y »).
Логические значения связки Лукасевича описываются следующей таблицей истинности:
2. Равносильности, выражающие основные законы алгебры логики:
· 
– коммутативность конъюнкции;
· 
– коммутативность дизъюнкции;
· 
– ассоциативность конъюнкции;
· 
– ассоциативность дизъюнкции;
· 
– дистрибутивность конъюнкции относительно дизъюнкции;
· 
– дистрибутивность дизъюнкции относительно конъюнкции.
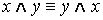
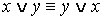
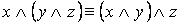
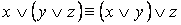
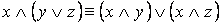
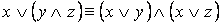
Замечание. Равносильности группы 3 показывают, что над формулами алгебры логики можно проводить те же преобразования, что и в алгебре чисел.
Равносильные преобразования формул
Используя равносильности групп 1–3 можно часть формулы или формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными.
Равносильные преобразования используются для доказательства равносильностей , для приведения формул к заданному виду, для упрощения формул. Формула A считается проще равносильной ей формулы B , если она содержит меньше букв, меньше логических операций. При этом обычно операции эквивалентность и импликация заменяются операциями дизъюнкции и конъюнкции, а отрицание относят к элементарным высказываниям.
Источник
Каким способом можно определить равносильность формул логики
Алфавит логики высказываний состоит из трех групп символов: высказывательные переменные a , b , c , d , …, x , y , z ; логические символы 
, 
, →, ↔, −; символы скобок ( , ). Словом в алфавите называется произвольная конечная последовательность символов.
Слово в алфавите логики высказываний называется формулой, если оно удовлетворяет следующему определению:
1) любая высказывательная переменная – формула;
2) если А и В формулы, то слова 
, 
, 
, 
, 
– формулы;
3) только те слова являются формулами, для которых это следует из 1) и 2).
Например: 
или 
. Скобки указывают порядок выполнения действий.
Скобки в формулах можно опускать, придерживаясь следующего порядка выполнения действий: коньюнкция, дизьюнкция, импликация и эквиваленция.
1) 
равносильно 
.
2) 
равносильно 
.
Логическое значение формулы полностью определяется логическими значениями входящих в нее элементарных высказываний.
При x = 1, y = 1, z = 0 формула 
Логическое значение формулы изменяется в зависимости от изменений значений элементарных высказываний, входящих в формулу. Все возможные логические значения формулы могут быть описаны полностью с помощью таблицы истинности.
Таблица истинности логических значений формулы 
будет следующая:
Если формула содержит n элементарных высказываний, то она принимает 2 n значений. Таблица истинности будет содержать 2 n строк.
Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения на любом наборе значений, входящих в формулы элементарных высказываний.
Обозначается равносильность ≡, т. е. A ≡ B .
Следующие формулы являются равносильными: 
Формула А называется тождественно истинной (или тавтологией ), если она принимает значение 1 при всех значениях входящих в нее переменных.
Следующие формулы являются тавтологиями: 
,
Формула А называется тождественно ложной , если она принимает значение 0 при всех значениях входящих в нее переменных.
Формула 
является тождественно ложной.
Отношение равносильности обладает следующими свойствами: оно рефлексивно, симметрично и транзитивно.
Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула 
– тавтология, и обратно, если формула – тавтология, то формулы А и В равносильны.
Равносильности алгебры логики используются для того, чтобы любую формулу алгебры логики можно заменить равносильной ей формулой.
Важнейшие равносильности алгебры логики можно разбить на три группы.
1. Основные равносильности
Докажем формулу 4.
Пусть А ≡ 
при x = 1, значение А = 1, при х = 0, значение А = 0. Итак во всех случаях значения формулы А совпадают со значениями х, следовательно, А ≡ х.
2. Равносильности, выражающие одни логические операции через другие
Замечание. Формулы 5 и 6 получаются из 3 и 4, если от обеих частей последних взять отрицания и воспользоваться законом снятия двойного отрицания.
Докажем формулы 1–4.
Докажем формулу 1.
1) при одинаковых логических значениях x и y формулы 
, 
и 
– истинны, следовательно, истинной будет и коньюнкция 
т. е. обе части равносильности имеют одинаковые истинные значения.
2) пусть теперь x и y имеют разные логические значения , тогда будут ложными 
и одна из или . При этом будет ложной и коньюнкция 
т. е. обе части равносильности имеют одинаковые ложные значения. Что и требовалось доказать.
Докажем формулу 3.
1) пусть x и y одновременно принимают истинные значения , тогда будет истинной и коньюнкция 
и ложным ее отрицание 
. В то же время будут ложными и , следовательно, будет ложной и дизьюнкция .
2) пусть хотя бы одна из переменных x или y принимает значение ложь, тогда тоже ложь, а – истина. В то же время отрицание хотя бы одной из переменных будет истинным, следовательно, будет истиной и дизьюнкция .
Следовательно, во всех случаях обе части равносильности 3 принимают одинаковые логические значения.
Аналогично доказываются равносильности 2 и 4.
Из равносильностей группы 2 следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: коньюнкцию и отрицание или дизьюнкцию и отрицание.
3. Равносильности, выражающие основные законы алгебры логики
– комм утативность коньюнкции и дизьюнкции.
Докажем формулу 6.
При х = 1, формулы , 
и 
будут истинны, тогда и 
– тоже истинна.
При х = 0, 
≡ 
, ≡ 
≡ 
следовательно, 
Таким образом, обе части формулы 6 равносильны одной и той же формуле 
и поэтому принимают одинаковые логические значения. Что и требовалось доказать.
Равносильности 3-ей группы выражают основные законы алгебры логики: коммутативность, ассоциативность и дистрибутивность (относительно логических операций – коньюнкции и дизьюнкции). Эти же законы имеют место в алгебре чисел. Поэтому над формулами алгебры логики можно производить те же преобразования, которые проводятся в алгебре чисел, т. е.
1) раскрытие скобок;
2) заключение в скобках;
3) вынесения за скобки общего множителя.
Кроме этих преобразований над формулами алгебры логики можно производить и преобразования, основанные на использовании равносильностей.
Равносильные преобразования формул используют
1) для доказательства равносильностей,
2) для приведения формул к заданному виду,
3) для упрощения формул.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций коньюнкции и дизьюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
1. Доказать равносильность
2. Упростить формулу
3. Доказать тождественную истинность формулы
Источник
