Каким способом можно определить мгновенную скорость тела

Как вычислить мгновенную скорость

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 18 человек(а).

Количество просмотров этой статьи: 71 748.

Скорость — это быстрота перемещения объекта в заданном направлении. [1] X Источник информации В общих целях нахождение скорости объекта (v) — простая задача: нужно разделить перемещение (s) в течение определенного времени (s) на это время (t), то есть воспользоваться формулой v = s/t. Однако таким способом получают среднюю скорость тела. Используя некоторые вычисления, можно найти скорость тела в любой точке пути. Такая скорость называется мгновенной скоростью и вычисляется по формуле v = (ds)/(dt), то есть представляет собой производную от формулы для вычисления средней скорости тела. [2] X Источник информации

• В этом уравнении: Перемещение = s. Перемещение — пройденный объектом путь. Например, если тело переместилось на 10 м вперед и на 7 м назад, то общее перемещение тела равно 10 — 7 = 3 м (а на 10 + 7 = 17 м). Время = t. Обычно измеряется в секундах.

s = -1.5t 2 + 10t + 4
(2)-1.5t (2-1) + (1)10t 1 — 1 + (0)4t 0
-3t 1 + 10t 0
-3t + 10

Источник

Мгновенная и средняя скорость

Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.

Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.

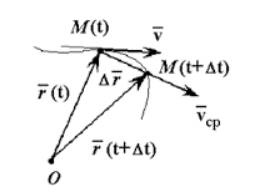
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения » open=» υ = ∆ r ∆ t ; » open=» υ ↑ ↑ ∆ r .

Рисунок 1 . Средняя скорость сонаправлена перемещению

Модуль средней скорости по пути равняется » open=» υ = S ∆ t .

Мгновенная скорость точки. Формулы

Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

Мгновенной скоростью называют предел, к которому стремится средняя скорость » open=» υ при стремлении промежутка времени ∆ t к 0 :

υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ .

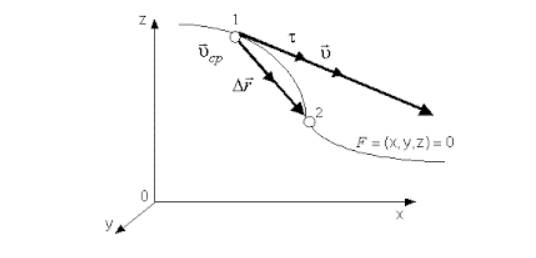
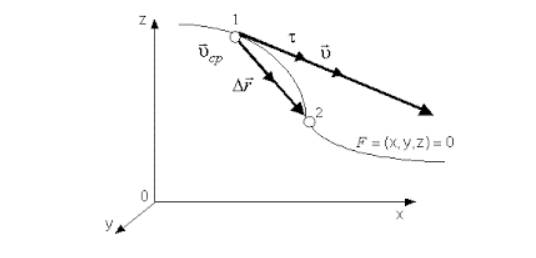
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение d r совпадает с бесконечно малым элементом траектории d s .

Рисунок 2 . Вектор мгновенной скорости υ

Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:

υ x = d x d t = x ˙ υ y = d y d t = y ˙ υ z = d z d t = z ˙ .

Перемещение и мгновенная скорость

Запись модуля вектора υ примет вид:

υ = υ = υ x 2 + υ y 2 + υ z 2 = x 2 + y 2 + z 2 .

Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = r q 1 , q 2 , q 3 , тогда значение скорости запишется как:

υ = d r d t = ∑ i = 1 3 ∂ r ∂ q i ∂ q i ∂ r = ∑ i = 1 3 ∂ r ∂ q i q ˙ i .

Рисунок 3 . Перемещение и мгновенная скорость в системах криволинейных координат

При сферических координатах предположим, что q 1 = r ; q 2 = φ ; q 3 = θ , то получим υ , представленную в такой форме:

υ = υ r e r + υ φ e φ + υ θ φ θ , где υ r = r ˙ ; υ φ = r φ ˙ sin θ ; υ θ = r θ ˙ ; r ˙ = d r d t ; φ ˙ = d φ d t ; θ ˙ = d θ d t ; υ = r 1 + φ 2 sin 2 θ + θ 2 .

Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t

Дан закон прямолинейного движения точки x ( t ) = 0 , 15 t 2 — 2 t + 8 . Определить ее мгновенную скорость через 10 секунд после начала движения.

Решение

Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:

υ ( t ) = x ˙ ( t ) = 0 . 3 t — 2 ; υ ( 10 ) = 0 . 3 × 10 — 2 = 1 м / с .

Ответ: 1 м / с .

Движение материальной точки задается уравнением x = 4 t — 0 , 05 t 2 . Вычислить момент времени t о с т , когда точка прекратит движение, и ее среднюю путевую скорость » open=» υ .

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

υ ( t ) = x ˙ ( t ) = 4 — 0 , 1 t .

4 — 0 , 1 t = 0 ; t о с т = 40 с ; υ 0 = υ ( 0 ) = 4 ; » open=» υ = ∆ υ ∆ t = 0 — 4 40 — 0 = 0 , 1 м / с .

Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0 , 1 м / с .

Источник

Каким способом можно определить мгновенную скорость тела

Графическое представление равномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

V (t) — изменение скорости со временем

S(t) — изменение перемещения (пути) со временем

a(t) — изменение ускорения со временем

За висимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно ( v = const ), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) — прямая линия, параллельная оси времени.

Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

Зависимость перемещения от времени. График s(t) — наклонная линия :

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Неравномерное прямолинейное движение.

Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.

Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

Различие между средней и мгновенной скоростями показано на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.

Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

V_x — Скорость тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

a_x — Ускорение тела

t — Время движения тела

Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Единица измерения ускорения в СИ [м/с 2 ].

Ускорение измеряют акселерометром

Уравнение скорости для равноускоренного движения: v_x = v_xo + a_xt

Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

S_x — Перемещение тела при равноускоренном движении по прямой

V_x o — Начальная скорость тела

V_x — Скорость тела при равноускоренном движении по прямой

a_x — Ускорение тела

t — Время движения тела

Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

— если известны начальная, конечная скорости движения и ускорение.

— если известны начальная, конечная скорости движения и время всего движения

Графическое представление неравномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

V(t) — изменение скорости со временем

S(t) — изменение перемещения (пути) со временем

a(t) — изменение ускорения со временем

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости v_x = v_xo + a_xt . Графиком является наклонная линия.

Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.

Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:

В координатах зависимость имеет вид:

Источник

I. Механика

Тестирование онлайн

Виды неравномерного движения

Неравномерным считается движение с изменяющейся скоростью. Скорость может изменяться по направлению. Можно заключить, что любое движение НЕ по прямой траектории является неравномерным. Например, движение тела по окружности, движение тела брошенного вдаль и др.

Скорость может изменяться по численному значению. Такое движение тоже будет неравномерным. Особенный случай такого движения — равноускоренное движение.

Иногда встречается неравномерное движение, которое состоит из чередования различного вида движений, например, сначала автобус разгоняется (движение равноускоренное), потом какое-то время движется равномерно, а потом останавливается.

Мгновенная скорость

Охарактеризовать неравномерное движение можно лишь скоростью. Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени. Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!

Средняя скорость

Что же такое средняя скорость? Неверно думать, что необходимо сложить все мгновенные скорости и разделить на их количество. Это самое распространенное заблуждение о средней скорости! Средняя скорость — это весь путь разделить на затраченное время. И никакими другими способами она не определяется. Если рассмотреть движение автомобиля, можно оценить его средние скорости на первой половине пути, на второй, на всем пути. Средние скорости могут быть одинаковыми, а могут быть различными на этих участках.

У средних величин рисуют сверху горизонтальную черту.

Средняя скорость перемещения. Средняя путевая скорость

Если движение тела не является прямолинейным, то пройденный телом путь будет больше, чем его перемещение. В этом случае средняя скорость перемещения отличается от средней путевой скорости. Путевая скорость — скаляр.

Главное запомнить

1) Определение и виды неравномерного движения;
2) Различие средней и мгновенной скоростей;
3) Правило нахождения средней скорости движения

Формула для определения средней скорости*

Часто требуется решить задачу, где весь путь разбит на равные участки, даны средние скорости на каждом участке, требуется найти среднюю скорость движения на всем пути. Неверное решение будет, если сложить средние скорости и разделить на их количество. Ниже выводится формула, которую можно использовать при решении подобных задач.

Определение мгновенной скорости графически*

Мгновенную скорость можно определить с помощью графика движения. Мгновенная скорость тела в любой точке на графике определяется наклоном касательной к кривой в соответствующей точке. Мгновенная скорость — тангенс угла наклона касательной к графику функции.

Упражнения

Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?

Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.

Какую скорость переменного движения показывает спидометр автомобиля?

Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.

В каком случае мгновенная и средняя скорости равны между собой? Почему?

При равномерном движении. Потому что скорость не изменяется.

Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?

Поезд прошел путь между городами со скоростью 50км/ч. Какая это скорость: средняя или мгновенная?

*Два шарика начали одновременно и с одинаковой скоростью двигаться по поверхностям, имеющим форму, изображенную на рисунке. Как будут отличаться скорости и время движения шариков к моменту их прибытия в точку В? Силу трения не учитывать.

Задача решается графическим способом. Скорости будут одинаковы. Время движения второго шарика меньше. Примерные графики движения шариков приведены на рисунке. Так как пути. пройденные шариками, равны, то, как видно из графика (на графике пути численно равны площадям заштрихованных фигур), время второго шарика меньше времени первого.

Источник