- Каким способом можно изменить внутреннюю энергию тела ответ нагреть его поднять его
- Внутренняя энергия тела и способы её изменения
- Урок 2. Физика 8 класс (ФГОС)
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Внутренняя энергия тела и способы её изменения»
Каким способом можно изменить внутреннюю энергию тела ответ нагреть его поднять его
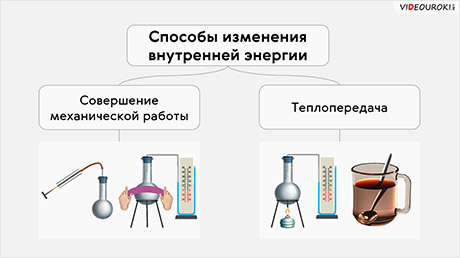
Внутреннюю энергию тела можно изменить:
1) теплопередачей (теплопроводностью, конвекцией и излучением);
2) совершением механической работы над телом (трение, удар, сжатие и др.).
Энергия тела, которую оно получает или отдаёт при обмене теплом с другими телами (без совершения работы), называют количеством теплоты.
$$ = \Delta U$$ — количество теплоты. | (8) |
Рассмотрим эти процессы более подробно.
1. Виды теплопередачи
А)
явление передачи теплоты (энергии) от одной части тела (более нагретой) к другой (менее нагретой).
Передача теплоты осуществляется в основном за счёт колебательного движения и столкновения отдельных молекул. При этом при столкновениях некоторая доля кинетической энергии молекул от одной (более нагретой) части тела передаётся молекулам другой (менее нагретой) его части. Важно заметить, что при теплопроводности само вещество не перемещается, а теплопередача всегда идёт в определённом направлении: внутренняя энергия горячего тела уменьшается, а внутренняя энергия холодного тела увеличивается.
В твёрдых металлических телах теплопроводность осуществляется преимущественно за счёт движущихся особым образом свободных электронов (в металлах также осуществляется перенос тепла колеблющимися атомами, но их вклад сравнительно небольшой).
Благодаря непрерывному взаимодействию соседствующих молекул, теплопроводность в твёрдых телах и жидкостях происходит заметно быстрее, чем в газах.
Интенсивность теплопроводности между телами зависит от разности их температур, площади поверхности, через которую происходит теплопередача, а также от свойств вещества, расположенного между телами.
В обычных условиях для расчёта количества теплоты `Q`, передаваемого через слой вещества путём теплопроводности, пользуются следующим соотношением:
| Здесь | $$ k$$ – коэффициент теплопроводности вещества слоя, |
| $$ S$$ – площадь поверхности, через которую происходит теплопередача (см. рис 3), | |
| $$ h$$ – толщина слоя вещества, | |
| $$ t$$ – время наблюдения, | |
| $$ \Delta T= |
Например, тепловая энергия уходит из комнаты через стену на улицу.
$$ S$$ – площадь поверхности стены,
- $$ h$$ – толщина слоя вещества, составляющего стену.
- $$ \Delta T$$ – разность температур между комнатой $$ \left(
_<1>\right)$$ и улицей $$ \left( _<2>\right)$$;
$$ k$$ – коэффициент теплопроводности вещества стены.
Следует отметить, что значения коэффициентов теплопроводности различных веществ отличаются столь сильно, что некоторые вещества применяют как эффективные теплопроводники (металлы, термомастика), а другие, наоборот, как теплоизоляторы (кирпич, дерево, пенопласт).
Б) В поле силы тяжести ещё одним механизмом теплопередачи может служить конвекция.
называют процесс перемешивания вещества, осуществляемый силой Архимеда, вследствии разности температур.
Конвекция может быть обнаружена в газах, жидкостях или сыпучих материалах.
Например, в кастрюле (см. рисунок 4) нагреваемая снизу вода расширяется, плотность её уменьшается. Сила Архимеда, действующая на небольшой фрагмент прогретой воды, поднимает её вверх. На поверхности прогретая вода остывает, смешиваясь с более холодной водой, испаряясь и т. п. Вследствие чего вода сжимается, становится более плотной, и тонет. Возникает конвективная ячейка.
На практике часто встречается принудительная конвекция, осуществляемая насосами или специальными перемешивающими механизмами.
В) Все тела, температура которых отлична от абсолютного нуля, излучают электромагнитные волны, которые переносят энергию. При комнатной температуре это в основном инфракрасное излучение. Так происходит лучистый теплообмен, или теплопередача посредством теплового излучения.
Из этого факта вытекает, что энергией в форме излучения обмениваются практически все окружающие нас тела. Этот процесс также приводит к выравниванию температур тел, участвующих в теплообмене.
Согласно теории равновесного теплового излучения интенсивность $$ I$$ излучения так называемого абсолютно чёрного тела пропорциональна четвёртой степени абсолютной температуры $$ T$$ тела:
| $$I=\sigma · | (10) |
Где `sigma=5,67*10^(-8)` `»Вт»//»м»^2«»К»^4` — постоянная Стефана-Больцмана.
(Подробно речь об этом пойдёт в разделе «Основы квантовой физики» в 11 классе.)
В замкнутой системе теплообмен должен привести к установлению теплового равновесия. Теперь понятию «замкнутой системы» можно придать более отчётливые очертания: если границы некоторой области пространства имеют очень малый коэффициент теплопроводности (граница – слой теплоизолятора) и теплопередача через него не проходит, то содержащаяся внутри области пространства энергия изменяться не может и будет сохраняться.
2. Работа и изменение внутренней энергии.
Работа газа при расширении и сжатии
Для изменения внутренней энергии тела необходимо изменить кинетическую или потенциальную энергию его молекул. Этого можно добиться, не только при теплопередаче, но и деформируя тело. При упругой деформации изменяется расположение молекул или атомов внутри тела, приводящее к изменению сил взаимодействия (а значит, и потенциальной энергии взаимодействия), а при неупругой изменяются и амплитуды колебаний молекул или атомов, что изменяет кинетическую энергию молекул или атомов.
При ударе молотком по свинцовой пластине молоток заметно деформирует поверхность свинца (рис. 5). Атомы поверхностных слоёв начинают двигаться быстрее, внутренняя энергия пластины увеличивается.
Стоя на улице в морозную погоду и потирая руки, мы совершаем работу, что также приводит к увеличению внутренней энергии. Если сила трения возникла из-за взаимодействия шероховатостей, то при прохождении одной шероховатости мимо другой возникают колебания частей тела. Энергия колебаний превращается в тепло. Тот же процесс происходит и при разрывах шероховатостей.
Если работу совершает газ, закрытый в цилиндре и поршень будет перемещаться из положения `1` в положение `2` (рис. 6), то работа равна
Здесь $$ F$$ – сила, действующая на поршень со стороны газа,
- $$ p$$ – давление газа,
- $$ S$$ – площадь поверхности поршня,
$$ \Delta V$$ – изменение объёма газа.
В некоторых случаях для расчёта работы газа в тепловом процессе удобно воспользоваться графическим методом . Суть его можно представить следующим образом. Допустим, что газ изобарно расширяется от начального объёма $$
Нетрудно убедиться, что $$ <>^<">S< >^<">=^<\text<'>>$$, т. е. работа газа при расширении от объёма $$
Если же процесс является более сложным (см. рис. 8), то и в этом случае графически работу можно найти как площадь фигуры под графиком процесса `1–2`.
Докажем это, рассмотрев переход газа из состояния 1 в состояние 2 не по кривой, а по ломаной, состоящей из $$ N$$ отрезков изохор и изобар. Работа на $$ i$$-ой изобаре (на рисунке $$ i=5$$) равна $$ _=
_·\Delta
Эту работу можно вычислить точнее, если увеличить число изобар и изохор ломаной (увеличить $$ N$$ и уменьшить $$ \Delta
так как к площади заштрихованной фигуры добавятся новые площади. Если число изобар и изохор устремить к бесконечности так, чтобы длина отрезков любой изобары и изохоры неограниченно уменьшалась, то ломаная линия совпадёт с кривой. Это и доказывает утверждение о том, что графически работу газа можно вычислить, найдя площадь фигуры под графиком процесса. Аналогично подсчитывают работу газа при его сжатии (уменьшении объёма). Необходимо только помнить, что работа газа в этом случае отрицательна.
При разбиении фигуры, образованной графиком процесса, изохорами и осью объёмов, на бесконечно малые элементы, изменение объёма записывается как $$ dV$$ (рис. 9). В этом случае малый элемент общей работы (элементарную работу) можно найти как $$ dA=p·dV$$, а всю работу получим суммированием всех элементарных работ на участке расширения:
Работа газа численно равна площади фигуры под графиком $$ p\left(V\right)$$.
Если идеальный газ находится в теплоизолированном сосуде (стенки сосуда не пропускают тепло), то работа внешней силы, совершённая над ним, равна изменению кинетически энергий молекул газа, т. е. равна изменению его внутренней энергии:
В рамках молекулярно-кинетической теории этот факт можно пояснить следующим образом. При столкновении молекулы с движущимся навстречу ей массивным поршнем перпендикулярная к поршню составляющая скорости молекулы увеличится на удвоенную скорость поршня.
Источник
Внутренняя энергия тела и способы её изменения
Урок 2. Физика 8 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Внутренняя энергия тела и способы её изменения»
Вы знаете, что существует два вида механической энергии — кинетическая и потенциальная. Давайте вспомним, что кинетической энергией обладает всякое движущееся тело: 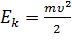
Потенциальная энергия определяется взаимным положением взаимодействующих тел или отдельных частей тела: Eп = mgh.
Изучая механические явления, вы узнали, что кинетическая и потенциальная энергии могут превращаться друг в друга таким образом, что их сумма остаётся постоянной величиной: E = Ek + Eп = const.
В этом заключается один из наиболее общих и фундаментальных законов природы — закон сохранения и превращения энергии.
Однако, вы знаете, что в реальных опытах закономерности превращения энергии выглядят гораздо сложнее.
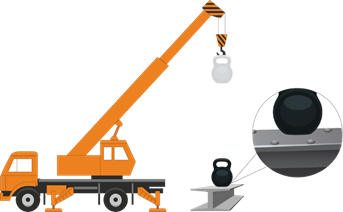
Например, возьмём гирю из какого-либо мягкого металла, например, из свинца, и стальную плиту. Поднимем гирю вверх на какую-либо высоту, тем самым сообщив ей некоторый запас потенциальной энергии. А затем отпустим. Во время полёта гири её потенциальная энергия уменьшается, а кинетическая, наоборот, увеличивается. После падения, гиря остановится. Её потенциальная энергия относительно плиты равна нулю, как равна нулю и кинетическая энергия, поскольку гиря неподвижна. Означает ли это, что нарушился основной закон природы, и энергия бесследно исчезла?
Конечно же нет. Механическая энергия перешла в другой вид энергии. Если внимательно посмотреть на гирю после удара, то мы обнаружим, что она, как и плита, слегка сплющилась, то есть деформировалась. А если мы измерим её температуру до и после падения, то окажется, что она увеличилась.
Мы уже знаем, что при изменении температуры тела, изменяется скорость движения его молекул. Помимо этого, в результате деформации гири, изменилось и взаимное расположение молекул друг относительно друга. Значит изменилась и их потенциальная энергия.
Следовательно, механическая энергия, которой обладала гиря в начале опыта, не исчезла: она перешла в потенциальную и кинетическую энергию её молекул.
Сумма кинетической энергии теплового движения частиц, из которых состоит тело, и потенциальной энергии их взаимодействия, называется внутренней энергией тела.
Обозначают внутреннюю энергию буквой U. А измеряют её в тех же единицах, что и механическую энергию: [U] = [Дж].
Возникает логичный вопрос: а каково значение внутренней энергии какого-либо тела?
Для примера рассмотрим какой-нибудь газ, например, кислород. Потенциальная энергия взаимодействия его молекул между собой практически отсутствует. А кинетическая энергия одной молекулы кислорода очень мала. Расчёты показывают, что среднее значение кинетической энергии молекулы кислорода при комнатной температуре равно 3,7 ∙ 10 −21 Дж.
Кто-то скажет, что это очень маленькая величина, и будет прав. Но, например, в 1 м 3 газообразного кислорода содержится примерно 2,7 ∙ 10 25 . А их общая энергия равна почти 100 кДж. А это значение энергии уже весьма значительно. Такой энергией, например, будет обладать одна тонный бизон, если его поднять на высоту десяти метров.
Теперь выясним, от чего зависит внутренняя энергия тела?
Вы уже знаете, что чем больше температура тела, тем быстрее движутся молекулы. Чем больше скорость движения, тем больше их кинетическая энергия. Значит, внутренняя энергия тела зависит от его температуры.
Также вам должно быть известно, что для перевода вещества из жидкого состояния в газообразное, например, чтобы превратить воду в пар, нужно подвести энергию. Следовательно, пар будет обладать большей внутренней энергией, чем вода той же массы. Значит, внутренняя энергия тела при неизменной массе зависит от его агрегатного состояния.
Т. к. масса тела равна сумме масс составляющих его частиц, то внутренняя энергия зависит и от массы тела.
Но внутренняя энергия тела не зависит от его механического движения и от его взаимодействия с другими телами. Так, например, внутренняя энергия мяча, лежащего на полу и поднятого на некоторую высоту от пола, одинакова, так же, как и мяча, неподвижного и катящегося по полу (если, конечно, пренебречь силами сопротивления его движению).
Возникает вопрос, а может ли у тела отсутствовать внутренняя энергия?
Чтобы правильно на него ответить, достаточно вспомнить, что движение частиц, из которых состоит тело, никогда не прекращается, даже при очень низких температурах. Поэтому тело всегда обладает внутренней энергией.
Как правило, значение внутренней энергии в большинстве случаев вычислить очень трудно, поскольку каждое тело состоит из огромного числа частиц. Однако нас чаще будет интересовать не само значение внутренней энергии, а её изменение. А о нём можно судить, в частности, по значению совершённой работы.
Вот мы и подошли ко второй важной проблеме — можно ли как-то изменить внутреннюю энергию тела?
Рассуждаем последовательно. Внутренняя энергия определяется энергией движения и энергией взаимодействия частиц. Следовательно, если мы сможем изменить скорость движения частиц, либо усилить или ослабить их взаимодействие друг с другом, то мы сможем изменить и внутреннюю энергию тела.
Рассмотрим каждую из возможностей изменения внутренней энергии отдельно.
Мы уже знаем, что изменить кинетическую энергию частиц тела можно путём увеличения или уменьшения температуры тела.
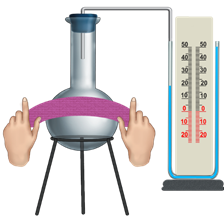
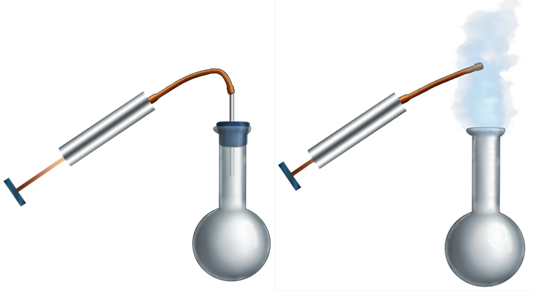
Существует два способа это сделать. Рассмотрим их на конкретных примерах. И так, возьмём закрытый сосуд с воздухом, к которому присоединим манометр. И начнём натирать сосуд с помощью тряпочки или сукна.
Уровень жидкости в левом колене манометра начинает понижаться. Это обусловлено тем, что воздух в колбе начинает нагреваться, вследствие чего, увеличивается его давление. Значит увеличивается и кинетическая энергия молекул воздуха. Таким образом, совершив механическую работу (трение сукна о колбу) мы смогли увеличить кинетическую энергию молекул находящегося в колбе воздуха.
Проделаем ещё один опыт. Возьмём толстостенный стеклянный сосуд, на дне которого находится небольшое количество воды. Закроем его пробкой с пропущенной через неё трубкой. Соединим трубку с насосом и начнём накачивать в сосуд воздух. Через некоторое время пробка из сосуда вылетит и в нём образуется туман.
Туман — это превратившийся в воду водяной пар.
Подумайте, когда образуется туман? Наверняка каждый из вас замечал, что чаще всего туман образуется тогда, когда после тёплого дня, наступает прохладная ночь, т. е. при значительном понижении температуры.
Следовательно, температура воздуха в сосуде понизилась. А понизилась она из-за того, что воздух, находящийся в сосуде, совершил работу. Вследствие чего, внутренняя энергия молекул воздуха в сосуде уменьшилась.
Таким образом, мы с вами можем сделать важный вывод о том, что внутренняя энергия тела изменяется при совершении работы. При этом если тело совершает работу, то его внутренняя энергия уменьшается. А если над телом совершают работу, то его внутренняя энергия увеличивается.
Теперь подумаем, можно ли изменить внутреннюю энергию тела, без совершения механической работы?
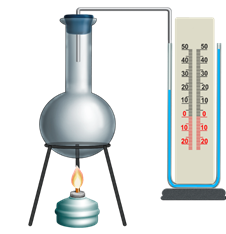
Вернёмся к опыту с колбой и манометром. Теперь не будем натирать колбу, а нагреем в ней воздух при помощи спиртовки. И опять через небольшой промежуток времени уровень жидкости в левом колене манометра начнёт понижаться. Что свидетельствует о том, что опять происходит изменение внутренней энергии воздуха в колбе.
Теперь обратимся к ситуации, с которой вы сталкиваетесь в жизни постоянно. Возьмём стакан с горячим чаем и металлическую ложку. Вы хорошо знаете, что если ложку опустить в стакан с чаем, то она через некоторое время тоже становится горячей.
В этом случае, как и в предыдущем, работа не совершается, но внутренняя энергия ложки увеличивается, о чём и свидетельствует повышение её температуры.
Поскольку вначале температура воды выше, чем температура ложки, то и средняя скорость молекул воды больше. А это значит, что молекулы воды обладают большей кинетической энергией, чем частицы металла, из которого сделана ложка. При столкновении с частицами металла молекулы воды передают им часть своей энергии, и кинетическая энергия частиц металла увеличивается. А кинетическая энергия молекул воды при этом уменьшается.
В рассмотренных нами примерах внутренняя энергия тел изменялась путём теплопередачи.
Теплопередача — способ изменения внутренней энергии тела, при котором энергия передаётся от одной части тела к другой или от одного тела к другому без совершения работы.
Стоит обратить внимание на то, что процесс теплопередачи происходит в определённом направлении — от более нагретых тел к менее нагретым, но не наоборот. А когда температуры тел выравниваются, теплопередача прекращается.
Таким образом, возможны два способа изменения внутренней энергии —совершение механической работы и теплопередача.
Существует три вида теплопередачи — теплопроводность, конвекция и излучение. Но о них мы с вами поговорим на следующих занятиях.
Источник