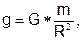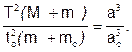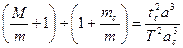Каким способом можно изменить массу небесного тела

Каким способом можно изменить массу небесного тела

§ 58. Определение масс небесных тел

Закон всемирного тяготения Ньютона позволяет измерить одну из важнейших физических характеристик небесного тела — его массу.

Массу небесного тела можно определить: а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ); б) по третьему (уточненному) закону Кеплера; в) из анализа наблюдаемых возмущений, производимых небесным. телом в движениях других небесных тел.

Первый способ применим пока только к Земле и заключается в следующем.

На основании закона тяготения ускорение силы тяжести на поверхности Земли

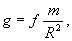
где т — масса Земли, a R — ее радиус. Отсюда масса Земли

Ускорение силы тяжести g (точнее, ускорение составляющей силы тяжести, обусловленной только силой притяжения), так же как и радиус Земли R , определяется из непосредственных измерений на поверхности Земли (см. § 46 и 62). Постоянная тяготения f достаточно точно определена из опытов Кэвендиша и Йолли, хорошо известных в физике.

С принятыми в настоящее время значениями величин g , R и f по формуле (2.25) получается масса Земли

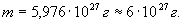
Зная массу Земли и ее объем, легко найти среднюю плотность Земли. Она равна 5,52 г/см 3

Третий, уточненный закон Кеплера позволяет определить соотношение между массой Солнца и массой планеты, если у последней имеется хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг нее.

Действительно, движение спутника вокруг планеты подчиняется тем же законам, что и движение планеты вокруг Солнца и, следовательно, уравнение (2.24) может быть записано в этом случае так:

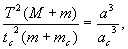
где — М, т и m_c — массы Солнца, планеты и ее спутника, Т и t_c — периоды обращений планеты вокруг Солнца и спутника вокруг планеты, a и а_с — расстояния планеты от Солнца и спутника от планеты соответственно.

Разделив числитель и знаменатель левой части дроби этого уравнения па т и решив его относительно масс, получим

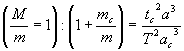
Отношение для всех планет очень велико; отношение же наоборот, мало (кроме Земли и ее спутника Луны) и им можно пренебречь. Тогда в уравнении (2.26) останется только одно неизвестное отношение , которое легко из него определяется. Например, для Юпитера определенное таким способом обратное отношение равно 1 : 1050.

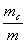
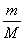
Так как масса Луны, единственного спутника Земли, сравнительно с земной массой достаточно большая, то отношением 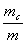в уравнении (2.26) пренебрегать нельзя. Поэтому для сравнения массы Солнца с массой Земли необходимо предварительно определить массу Луны. Точное определение массы Луны является довольно трудной задачей, и решается она путем анализа тех возмущений в движении Земли, которые вызываются Луной.

Под влиянием лунного притяжения Земля должна описывать в течение месяца эллипс вокруг общего центра масс системы Земля — Луна.

По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые “лунным неравенством”. Наличие “лунного неравенства” в видимом движении Солнца указывает на то, что центр Земли действительно описывает небольшой эллипс в течение месяца вокруг общего центра масс “Земля — Луна”, расположенного внутри Земли, на расстоянии 4650 км от центра Земли. Это позволило определить отношение массы Луны к массе Земли, которое оказалось равным 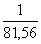. 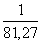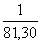Положение центра масс системы “Земля — Луна” было найдено также из наблюдений малой планеты Эрос в 1930—1931 гг. Эти наблюдения дали для отношения масс Луны и Земли величину . Наконец, по возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось равным . Последнее значение наиболее точное, и в 1964 г. Международный астрономический союз принял его как окончательное в числе других астрономических постоянных. Это значение подтверждено в 1966 г. вычислением массы Луны по параметрам обращения ее искусственных спутников.

С известным отношением масс Луны и Земли из уравнения (2.26) получается, что масса Солнца M _¤ в 333 000 раз больше массы Земли, т.е.

Зная массу Солнца и отношение этой массы к массе любой другой планеты, имеющей спутника, легко определить массу этой планеты.

Массы планет, не имеющих спутников (Меркурий, Венера, Плутон), определяются из анализа тех возмущений, которые они производят в движении других планет или комет. Так, например, массы Венеры и Меркурия определены по, тем возмущениям, которые они вызывают в движении Земли, Марса, некоторых малых планет (астероидов) и кометы Энке — Баклунда, а также по возмущениям, производимым ими друг на друга.

Источник

Методы определения масс небесных тел.

Закон всемирного тяготения Ньютона позволяет измерить одну из важнейших физических характеристик небесного тела — его массу.

Массу можно определить:

а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ),

б) по третьему уточнённому закону Кеплера,

в) из анализа наблюдаемых возмущений, производимых небесным телом в движениях других небесных тел.

1. Первый способ применяется на Земле.

На основании закона тяготения ускорение g на поверхности Земли:

где m — масса Земли, а R — её радиус.

g и R измеряются на поверхности Земли. G = const.

С принятыми сейчас значениями g, R, G получается масса Земли:

m = 5,976 .1027г = 6 .1024кг.

Зная массу и объём, можно найти среднюю плотность. Она равна 5,5 г/см3.

2. По третьему закону Кеплера можно определить соотношение между массой планеты и массой Солнца, если у планеты есть хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг неё.

где M, m, mc- массы Солнца, планеты и её спутника, T и tc- периоды обращений планеты вокруг Солнца и спутника вокруг планеты, а и ас— расстояния планеты от Солнца и спутника от планеты соответственно.

Из уравнения следует

Отношение М/m для всех планет очень велико; отношение же m/mc, очень мало (кроме Земли и Луны, Плутона и Харона) и им можно пренебречь.

Соотношение М/m можно легко найти из уравнения.

Для случая Земли и Луны нужно сначала определить массу Луны. Это сделать очень сложно. Решается задача путём анализа возмущений в движении Земли, которые вызывает Луна.

3. По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые «лунным неравенством». Наличие этого факта в видимом движении Солнца указывает на то, что центр Земли описывает небольшой эллипс в течение месяца вокруг общего центра масс «Земля — Луна», расположенного внутри Земли, на расстоянии 4650 км. от центра Земли.

Положение центра масс Земля-Луна было найдено также из наблюдений малой планеты Эрос в 1930 — 1931 гг.

По возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось 1/81,30.

В 1964 году Международный астрономический союз принял его как const.

Из уравнения Кеплера получаем для Солнца массу = 2.1033г., что в 333000 раза превосходит земную.

Массы планет, не имеющих спутников, определены по возмущениям, которые они вызывают в движении Земли, Марса, астероидов, комет, по возмущениям, производимым ими друг на друга.

Дата добавления: 2014-12-17 ; просмотров: 6745 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Методическая разработка урока «Определение масс небесных тел»

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Определение масс небесных тел.docx

Класс:11 Урок № Дата:

Тема: Определение масс небесных тел.

Цели и задачи урока:

образовательные: изучить различные способы и методы измерения массы небесных тел; использовать решение задач для продолжения формирования расчетных навыков.

развивающие: показать учащимся, что законы открытые Ньютоном и Кеплером используются для глубокого познания природы и решения практических задач; развивать элементы творческого поиска на основе приёма анализа изучаемого материала; развивать умения сравнивать, анализировать и делать выводы.

воспитательные: формирование научного мировоззрения в ходе знакомства с историей человеческого познания и объяснения причин небесных явлений

Тип урока: комбинированный урок.

Межпредметные связи: физика, математика.

Оборудование и материалы: таблицы, презентация, видеоматериалы.

I . Организационный этап урока (1мин). Приветствие учащихся, проверка готовности к уроку. Настрой на восприятие учебного материала.

Учитель: «Мы продолжаем изучение небесных тел. И сегодня на уроке мы ответим на вопрос, которых многих интересует уже давно».

II . Целеполагание (2 мин) (используется приём «Отгадай») (Слайд №1). Чтобы сформулировать тему урока, отгадайте пропущенное слово:

«Измерение (в названии планеты, нашего ближайшего «соседа», названного в честь римского бога войны, третью букву замените на четвёртую) небесных тел». (записывают в тетрадь дату и тему урока). Сформулируем задачи урока(учащиеся с помощью учителя формулируют задачи, стоящие на уроке).

III . Мотивационный этап урока (1мин) (используется проблемная ситуация) (Слайд №1). Вам известен такой способ измерения массы, как взвешивание. Но можно ли его применить, если речь идёт о небесных телах (учащиеся отвечают, что простое взвешивание не применимо в данном случае). Как быть? Проблема.

IV . Актуализация опорных знаний (3мин) (используется приём «Найди ошибку») (Слайд №2).

Для решения поставленных задач повторим закон всемирного тяготения и третий закон Кеплера

V. Изучение нового материала (25мин) (используется работа с учебником и справочными материалами, а так же объяснение учителя и самостоятельная работа учащихся) (Слайды №№3,4).

Массы небесных тел можно определить разными способами:

а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ),

б) по третьему обобщенному закону Кеплера.

Рассмотрим первый способ (5мин) на примере определения массы Земли, используя материал учебника (В.М.Чаругин стр.53, п.1). Расположите формулы в порядке, приводящем к нужному результату: (Слайд №3).

Проверка полученных знаний (15мин): Рассчитайте массы планет солнечной системы и сравните их с табличным значением, используйте данные справочника (задание выполняют в парах, только учащиеся, работающие на «3») (Слайд №4).

Рассмотрим второй способ (5мин) (работа только с учащимися, работающими на «4» и «5»). Для этого используем обобщённый(уточнённый Ньютоном) закон Кеплера (записи на доске и в тетради)

Если две планеты движутся вокруг Солнца

T ₁ , T ₂ периоды обращения планет вокруг Солнца

а₁,а₂ среднее расстояние планет от Солнца

Если планета движется вокруг Солнца и спутник вокруг планеты

m масса планеты

m₁ масса спутника

T период обращения планет вокруг Солнца

T₁ период обращения спутника вокруг планеты

а среднее расстояние планет от Солнца

а₁ среднее расстояние спутника от планеты

Проверка полученных знаний (10мин): Рассчитайте массы тел солнечной системы и сравните их с табличным значением, используйте данные справочника.

Учащие, работающие на «4» рассчитывают массу Юпитера, используя первую формулу.

Учащиеся, работающие на «5» рассчитывают массу Луны, используя вторую формулу.

VII . Домашнее задание (2мин) (Слайд №5). Для учащихся, работающих на «3» изучить первый способ стр. 53 п.1, уметь им воспользоваться; для учащихся, работающих на «4и 5» изучить два способа и уметь ими воспользоваться; дополнительно(по желанию): подготовить сообщение ещё об одном способе определения массы небесных тел исходя из анализа наблюдаемых возмущений, производимых небесным телом в движениях других небесных тел.

Конспект изучить, дополнительно: подготовить сообщение еще об одном способе определения массы небесных тел.

VIII . Подведение итогов урока (2мин). Учитель словесно оценивает работу наиболее активных учащихся, выставляет отметки за работу на уроке. Ставит вопрос перед учащимися: Достигнуты ли цели урока? (учащимся показывают слайд № 1, по желанию отвечают, что было изучено на уроке)

записывают все, что понравилось на уроке, информация и формы работы, которые вызвали положительные эмоции, либо, по мнению ученика, могут быть ему полезны для достижения каких-то целей

записывают все, что не понравилось на уроке, показалось скучным, вызвало неприязнь, осталось непонятным, или информация, которая, по мнению ученика, оказалась для него не нужной, бесполезной

записывают все любопытные факты, о которых узнали на уроке, что бы еще хотелось узнать по данной проблеме, вопросы к учителю.

Выбранный для просмотра документ Презентация к уроку Определение массы небесных тел.pptx

Источник