ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Вопросы к экзамену
Для всех групп технического профиля
Список лекций по физике за 1,2 семестр
Я учу детей тому, как надо учиться
Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.
Урок 16. Лекция 16. Внутренняя энергия. Первое начало термодинамики
Наука о тепловых явлениях называется термодинамика. Термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств макроскопических систем.
При изучении основ термодинамики необходимо помнить следующие определения. Физическая система, состоящая из большого числа частиц — атомов или молекул, которые совершают тепловое движение и, взаимодействуя между собой, обмениваются энергиями, называется термодинамической системой.
Состояние термодинамической системы определяется макроскопическими параметрами, например удельным объемом, давлением, температурой.
Термодинамика рассматривает изолированные системы тел, находящиеся в состоянии термодинамического равновесия. Это означает, что в таких системах прекратились все наблюдаемые макроскопические процессы. Важным свойством термодинамически равновесной системы является выравнивание температуры всех ее частей.
Термодинамика рассматривает только равновесные состояния, т.е. состояния, в которых параметры термодинамической системы не меняются со временем.
Если термодинамическая система была подвержена внешнему воздействию, то в конечном итоге она перейдет в другое равновесное состояние. Такой переход называется термодинамическим процессом.
Термодинамическим процессом называется переход системы из начального состояния в конечное через последовательность промежуточных состояний.
Процессы бывают обратимыми и необратимыми.
Обратимым называется такой процесс, при котором возможен обратный переход системы из конечного состояния в начальное через те же промежуточные состояния, чтобы в окружающих телах не произошло никаких изменений. Обратимый процесс является физической абстракцией. Примером процесса, приближающегося к обратимому, является колебание тяжелого маятника на длинном подвесе. В этом случае кинетическая энергия практически полностью превращается в потенциальную, и наоборот. Колебания происходят долго без заметного уменьшения амплитуды ввиду малости сопротивления среды и сил трения.
Любой процесс, сопровождаемый трением или теплопередачей от нагретого тела к холодному, является необратимым. Примером необратимого процесса является расширение газа, даже идеального, в пустоту. Расширяясь, газ не преодолевает сопротивления среды, не совершает работы, но, для того чтобы вновь собрать все молекулы газа в прежний объем, т. е. привести газ в начальное состояние, необходимо затратить работу. Таким образом, все реальные процессы являются необратимыми.
Изменение внутренней энергии газа в процессе теплообмена и совершаемой работы.
Одним из важнейших понятий термодинамики является внутренняя энергия тела. Все макроскопические тела обладают энергией, заключенной внутри самих тел. С точки зрения молекулярно-кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом.
Внутренняя энергия – это сумма энергий молекулярных взаимодействий и энергии теплового движения молекул.
В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема (закон Джоуля).
Молекулярно-кинетическая теория приводит к следующему выражению для внутренней энергии одного моля идеального одноатомного газа (гелий, неон и др.), молекулы которого совершают только поступательное движение:
Поскольку потенциальная энергия взаимодействия молекул зависит от расстояния между ними, в общем случае внутренняя энергия 
U тела зависит наряду с температурой T также и от объема V: U = U(T, V).
Таким образом, внутренняя энергия системы зависит только от её состояния и является однозначной функцией состояния, внутренняя энергия U тела однозначно определяется макроскопическими параметрами, характеризующими состояние тела. Она не зависит от того, каким путем было реализовано данное состояние.
Внутреннюю энергию тела можно изменить разными способами:
Внутренняя энергия тела может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную).
Например, газ подвергается сжатию в цилиндре под поршнем площадью S. Поршень, сжимая газ, движется с некоторой скоростью v. Молекулы газа, беспорядочно двигаясь, ударяются о поршень. После упругого удара молекулы о поршень скорость молекулы возрастает, а значит возрастает и её кинетическая энергия, что приводит к увеличению внутренней энергии газа.
При сжатии газа его внутренняя энергия увеличивается за счет совершения поршнем механической работы. При расширении газа его внутренняя энергия уменьшается, превращаясь в механическую энергию поршня.
При сжатии газа внешние силы совершают над газом некоторую положительную работу A’.
В то же время силы давления, действующие со стороны газа на поршень, совершают работу
Если объем газа изменился на малую величину ΔV, то газ совершает работу pSΔx = pΔV, где p – давление газа, S – площадь поршня, Δx – его перемещение.
При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна.
В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:
или в пределе при ΔVi → 0: 
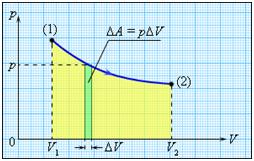
Работа численно равна площади под графиком процесса на диаграмме (p, V):
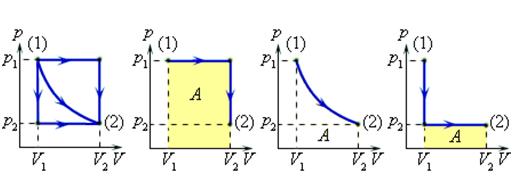
Величина работы зависит от того, каким путем совершался переход из начального состояния в конечное. На рис. 2 изображены три различных процесса, переводящих газ из состояния (1) в состояние (2). Во всех трех случаях газ совершает различную работу.
Рисунок 2.
Три различных пути перехода из состояния (1) в состояние (2).
Во всех трех случаях газ совершает разную работу, равную площади под графиком процесса.
Процессы, изображенные на рис. 2, можно провести и в обратном направлении; тогда работа A просто изменит знак на противоположный.
Процессы которые можно проводить в обоих направлениях, называются обратимыми.
В отличие от газа, жидкости и твердые тела мало изменяют свой объем, так что во многих случаях работой, совершаемой при расширении или сжатии, можно пренебречь. Однако, внутренняя энергия жидких и твердых тел также может изменяться в результате совершения работы. При механической обработке деталей (например, при сверлении) они нагреваются. Это означает, что изменяется их внутренняя энергия.
Внутренняя энергия тела может изменяться не только в результате совершаемой работы, но и вследствие теплообмена.
При тепловом контакте тел внутренняя энергия одного из них может увеличиваться, а внутренняя энергия другого – уменьшаться. В этом случае говорят о тепловом потоке от одного тела к другому. Передача энергии от одного тела другому в форме тепла может происходить только при наличии разности температур между ними.
Приведем в соприкосновение два тела с разными температурами. Пусть температура первого тела выше, чем второго. В результате обмена энергиями температура первого тела уменьшается, а второго — увеличивается. В рассматриваемом примере кинетическая энергия хаотического движения молекул первого тела переходит в кинетическую энергию хаотического движения молекул второго тела.
Тепловой поток всегда направлен от горячего тела к холодному.
Процесс передачи внутренней энергии без совершения механической работы называется теплообменом.
Мерой энергии, получаемой или отдаваемой телом в процессе теплообмена, служит физическая величина, называемая количеством теплоты.
Количеством теплоты Q, полученной телом, называют изменение внутренней энергии тела в результате теплообмена.
Количество теплоты Q является энергетической величиной. В СИ количество теплоты измеряется в единицах механической работы – джоулях (Дж).
До введения СИ количество теплоты выражали в калориях.
Калория — это количество теплоты, необходимое для нагревания 1 г дистиллированной воды на 1°С, от 19,5°С до 20,5°С.
Единица, в 1000 раз большая калории, называется килокалорией (1 ккал = 1000 кал). Соотношение между единицами: 1 кал =4,19 Дж.
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются.
Чтобы нагреть тело массой m от температуры t1 до температуры t2 ему необходимо сообщить количество теплоты
Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.
Во многих случаях удобно использовать молярную теплоемкость C:
C = M · c, где M – молярная масса вещества.
При передаче тепла от одного тела к другому всегда выполняется уравнение теплового баланса, по которому количество теплоты Q1, отданное первым телом, равно количеству теплоты Q2, полученному вторым телом.
Теплота и работа являются не видом энергии, а формой ее передачи, они существуют лишь в процессе передачи энергии.
В реальных условиях оба способа передачи энергии системе в форме работы и форме теплоты обычно сопутствуют друг другу.
Первое начало термодинамики.
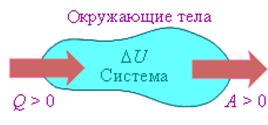
На рисунке изображены энергетические потоки между термодинамической системой и окружающими телами. в результате теплообмена и совершаемой работы:
Величина Q > 0, если тепловой поток нправлен в сторону термодинамической системы. Величина A > 0, если система совершает положительную работу над окружающими телами.
Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, то есть изменяются ее макроскопические параметры (температура, давление, объем).
Процессы теплообмена и совершения работы сопровождаются изменением ΔU внутренней энергии системы.
Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:
Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.
Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.
Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Если между телами, составляющими замкнутую систему, действуют силы трения, то часть механической энергии превращается во внутреннюю энергию тел (нагревание).
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Задачи для самостоятельного решения ( Дмитриева В.Ф. Задачи по физике)
Источник
Каким способом изменяется внутренняя энергия при сжатии газа
На рис. 3.9.1 условно изображены энергетические потоки между выделенной термодинамической системой и окружающими телами. Величина , если тепловой поток направлен в сторону термодинамической системы. Величина , если система совершает положительную работу над окружающими телами.
 | ||||||||||||||||||||
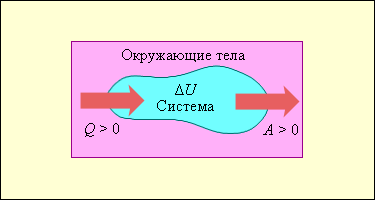| Рисунок 3.9.1. Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, т. е. изменяются ее макроскопические параметры (температура, давление, объем). Так как внутренняя энергия однозначно определяется макроскопическими параметрами, характеризующими состояние системы, то отсюда следует, что процессы теплообмена и совершения работы сопровождаются изменением внутренней энергии системы. Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом: Изменение внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты , переданной системе, и работой , совершенной системой над внешними телами.
Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами. Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода . Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу над внешними телами только за счет получения некоторого количества теплоты от окружающих тел или уменьшения своей внутренней энергии. Применим первый закон термодинамики к изопроцессам в газах. В изохорном процессе () газ работы не совершает, . Следовательно,
Здесь и – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (). В изобарном процессе ( ) работа, совершаемая газом, выражается соотношением
Первый закон термодинамики для изобарного процесса дает:
При изобарном расширении – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии – тепло отдается внешним телам. В этом случае . Температура газа при изобарном сжатии уменьшается, ; внутренняя энергия убывает, . В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, . Первый закон термодинамики для изотермического процесса выражается соотношением
Количество теплоты , полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам. Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками , а процессы расширения или сжатия газа в таких сосудах называются адиабатическими . В адиабатическом процессе ; поэтому первый закон термодинамики принимает вид
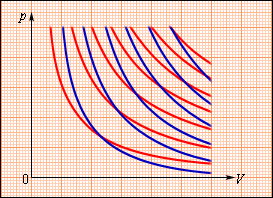
т. е. газ совершает работу за счет убыли его внутренней энергии. На плоскости () процесс адиабатического расширения (или сжатия) газа изображается кривой, которая называется адиабатой . При адиабатическом расширении газ совершает положительную работу (); поэтому его внутренняя энергия уменьшается (). Это приводит к понижению температуры газа. Вследствие этого давление газа при адиабатическом расширении убывает быстрее, чем при изотермическом (рис. 3.9.2).
|
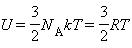
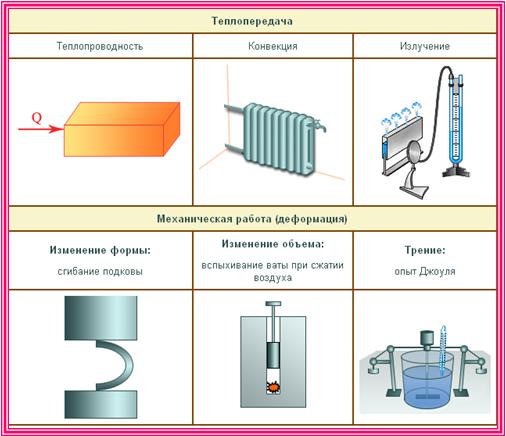
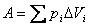
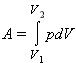
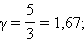для двухатомного 
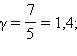для многоатомного 
