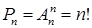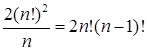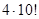Каким количеством способов можно посадить 6 человек за круглый стол

Сколькими способами можно рассадить 6 человек за столом по кругу

Добрый день.
Есть задача: Сколькими способами можно рассадить 6 человек за столом: а) в ряд; б) по кругу; в) по кругу, при условии, что места не имеют номеров?

Под а) получаю 6!=720
Под б) 6!/6=120
А вот под в) не очень понимаю. Разве будет как то отличаться от случая под буквой б)? Помогите пожалуйста.

Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два.

Сколькими способами можно рассадить в поезде 4 человек?
1. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человек при.

Сколькими способами можно разместить 8 человек за столом, у которого стоит 8 стульев?
Сколькома способами можно разместить 8 человек за столом, у которого стоит 8 стульев?

Сколькими способами 6 человек разместиться за столом, если имеет значение, на каком месте сидеть?
3. Решить задачу, используя а) правило произведения: б) формулы комбинаторики: Сколькими способами.

Сколькими способами можно рассадить этих людей?
На скамейке сидит 14 человек, среди которых три семьи: Петренко (4 чел.), Васюки (3 чел.) и.

Сколькими способами 10 мальчиков и 10 девочек можно рассадить
Сколькими способами 10 мальчиков и 10 девочек можно рассадить за 10 парт при условии, что за одной.

Сколькими способами можно рассадить этих людей?
3)среди 12 людей есть трое знакомых. Сколькими способами можно рассадить этих людей, чтобы знакомые.

Сколькими способами группу из 30 студентов можно рассадить по 36 стульям
Прошу проверить задание. Сколькими способами группу из 30 студентов можно рассадить по 36.

Сколькими способами можно рассадить этих людей, чтобы знакомые сидели рядом?
Помогите пожалуйста с задачами. Для закрытия всех долгов не хватает только этого 1. Среди 12.

Сколькими способами можно их рассадить за 10 партами, так чтобы за одной партой не сидели 2 девочки
В классе 12 мальчиков и 8 девочек. Сколькими способами можно их рассадить за 10 партами, так чтобы.

Источник

Сколькими способами можно рассадить 6 участников за круглым столом?

Математика | 10 — 11 классы

Сколькими способами можно рассадить 6 участников за круглым столом?

1) 6 * 5 * 4 * 3 * 2 * 1 = 720 вариантов ))))))))))))))))))))))))))).

Если участников собрания рассадить по 6 человек за каждый стол, то троим не хватить месть?

Если участников собрания рассадить по 6 человек за каждый стол, то троим не хватить месть.

А если этих же участников рассадить по 9 человек за каждый стол, то два стола останутся не занятыми.

Сколько человек участвовало на собрании?

У круглого стола поставили 4 стула?

У круглого стола поставили 4 стула.

Сколькими способами можно рассадить на эти стулья : а) 4 — х детей ; б) 3 — х детей ; в) 2 — х детей.

Если участников собрания рассадить по шесть человек на каждый стол, то троим не хватит месть?

Если участников собрания рассадить по шесть человек на каждый стол, то троим не хватит месть.

А если этих же участников рассадить по девять человек за каждый стол, то два стола останутся не занятыми.

Сколько человек участвовала на собрании?

Сколькими способами могут разместиться 5 человек вокруг круглого стола?

Сколькими способами могут разместиться 5 человек вокруг круглого стола.

Если участников собрания рассадить по 6 человек за каждый стол, то троим не хватит мест?

Если участников собрания рассадить по 6 человек за каждый стол, то троим не хватит мест.

А если этих же участников рассадить по 9 человек за каждый стол, то два стола останутся не занятыми.

Сколько человек участвовало на собрании?

За круглым столом расположились 30 взрослых участников дискуссии так, что правым соседом каждой женщины был мужчина, а у половины мужчин справа сидела женщина?

За круглым столом расположились 30 взрослых участников дискуссии так, что правым соседом каждой женщины был мужчина, а у половины мужчин справа сидела женщина.

Сколько женщин сидело за круглым столом?

За круглым столом 30 участников дискуссии сели так, что правым соседом каждой женщины был мужчина, а у половины мужчин справа сидела женщина?

За круглым столом 30 участников дискуссии сели так, что правым соседом каждой женщины был мужчина, а у половины мужчин справа сидела женщина.

Сколько женщин сидело за круглым столом?

Сколькими способами можно рассадить семь человек за круглый стол?

Сколькими способами можно рассадить семь человек за круглый стол.

Сколькими способами можно рассадить 7 лиц за столом, где поставлено 7 приборов?

Сколькими способами можно рассадить 7 лиц за столом, где поставлено 7 приборов.

У круглого стола поставили 4 стула?

У круглого стола поставили 4 стула.

Сколькими способами можно рассадить на эти стулья А) 4 ребёнка Б)3 ребёнка В)2 ребёнка.

На странице вопроса Сколькими способами можно рассадить 6 участников за круглым столом? из категории Математика вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Источник

07. Перестановки

Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.

Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.

Число перестановок n различных элементов обозначают символом Pn и равно

Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем

P6P4 = 720×24 = 17280.

Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?

Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно

4! – 3! = 3×3! = 3×1×2×3 = 18.

Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?

Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем .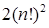

Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.

Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?

5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.

Ответ: .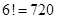

5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?

Ответ: .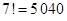

5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?

Ответ: .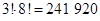

5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?

Ответ:

5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?

Ответ: .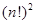

5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?

Ответ: .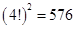

5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?

Ответ: .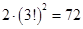

5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.

Источник

Сколькими способами можно рассадить 6 человек за столом по кругу — Комбинаторика — Ответ 13151076

Ответ

Я и под б) не слишком понимаю Ваше решение.
Если б) и в) отличаются тем, что в случае в) места не имеют номеров, тогда в случае б) места имеют номера.
А если места имеют номера, разве есть разница как они расположены в ряд, по кругу, или в шахматном порядке.
Разобравшись с этим, надо понять для в) какие рассадки являются одинаковыми, а какие разными. Т.е. чем отличаются разные рассадки между собой. От определения этого и зависит результат.

Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин?
Сколькими способами можно рассадить за круглым столом 5 мужчин и 5 женщин: 1) чтобы никакие два.

Сколькими способами можно рассадить в поезде 4 человек?
1. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человек при.

Сколькими способами можно разместить 8 человек за столом, у которого стоит 8 стульев?
Сколькома способами можно разместить 8 человек за столом, у которого стоит 8 стульев?

Сколькими способами 6 человек разместиться за столом, если имеет значение, на каком месте сидеть?
3. Решить задачу, используя а) правило произведения: б) формулы комбинаторики: Сколькими способами.

Сколькими способами можно рассадить этих людей?
На скамейке сидит 14 человек, среди которых три семьи: Петренко (4 чел.), Васюки (3 чел.) и.

Сколькими способами 10 мальчиков и 10 девочек можно рассадить
Сколькими способами 10 мальчиков и 10 девочек можно рассадить за 10 парт при условии, что за одной.

Сколькими способами можно рассадить этих людей?
3)среди 12 людей есть трое знакомых. Сколькими способами можно рассадить этих людей, чтобы знакомые.

Сколькими способами группу из 30 студентов можно рассадить по 36 стульям
Прошу проверить задание. Сколькими способами группу из 30 студентов можно рассадить по 36.

Сколькими способами можно рассадить этих людей, чтобы знакомые сидели рядом?
Помогите пожалуйста с задачами. Для закрытия всех долгов не хватает только этого 1. Среди 12.

Сколькими способами можно их рассадить за 10 партами, так чтобы за одной партой не сидели 2 девочки
В классе 12 мальчиков и 8 девочек. Сколькими способами можно их рассадить за 10 партами, так чтобы.

Источник

Каким количеством способов можно посадить 6 человек за круглый стол

В школьном курсе понятие «круговые перестановки» встречается в 7 классе в учебнике по алгебре в разделе «Для тех, кому интересно» [3].

В комбинаторных задачах часто ставится вопрос о том, сколькими способами можно расположить в ряд, или, как говорят математики, упорядочить, все элементы некоторого множества.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Получаемые при этом упорядоченные множества, которые отличаются друг от друга лишь порядком входящих в них элементов, называют перестановками без повторений из п элементовили «круговыми перестановками».

Из истории комбинаторики

Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, которые сейчас называют “сочетания”. В ХII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из п слогов. Как научная дисциплина, комбинаторика сформировалась в Х V II в. В книге “Теория и практика арифметики” (1656 г.) французский автор Андре Таке также посвящает сочетаниям и перестановкам целую главу.

Б. Паскаль в “Трактате об арифметическом треугольнике” и в “Трактате о числовых порядках” (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин “комбинаторика” стал употребляться после опубликования Лейбницем в 1665 г. работы “Рассуждение о комбинаторном искусстве”, в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги “Аг s соп j ес t ап d i” (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в ХIХ в [4].

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств — правило суммы и правило произведения. При решении задач на перестановки используется правило умножения.

Каждое расположение элементов множества в определенном порядке называют перестановкой. Рассмотрим задачу: В турнире четверо участников. Сколькими способами могут быть распределены места между ними?

Будем рассуждать в соответствии с правилом умножения. Первое место может занять любой из четырех участников. При этом второе место может занять любой из трех оставшихся, третье любой из двух оставшихся, а на четвертом месте останется последний участник. Значит, места между участниками могут быть распределены 4 ۰ 3 ۰ 2 ۰ 1 = 24 способами. Решив задачу, мы фактически подсчитали число перестановок для множества из четырех элементов. Рассуждая точно так же, можно показать, что для множества из пяти элементов число перестановок равно 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1, а для множества из десяти элементов это число равно 10 ۰ 9 ۰ 8 ۰ 7 ۰ б ۰ 5 ۰ 4 ۰ 3 ۰ 2 ۰ 1.

Вообще если множество содержит п элементов, то число перестановок равно произведению п(п – 1)(п – 2) ۰…۰ 2 ۰ 1. Множители в этом произведении можно записать в обратном порядке: 1 ۰ 2 ۰ . ۰ (п – 2)(п – 1)п.

Такие произведения бывают очень длинными и часто выражаются огромными числами. Однако в математике есть специальный символ для их обозначения. Произведение всех натуральных чисел от 1 до п обозначают п! (читают: «п факториал»). Значение выражения п! можно найти для любого натурального числа п (при этом считают, что 1! = 1).

Факториалы растут удивительно быстро. Можно понаблюдать за их изменением, рассмотрев таблицу, в которой приведены факториалы чисел от 1 до 10:

Источник