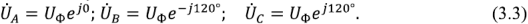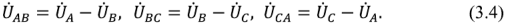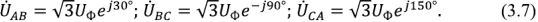- Варианты подключения обмоток трехфазных генераторов
- § 3.6. Соединение обмоток генератора трехфазного тока
- Соединение звездой
- Соединение обмоток генератора треугольником
- Способы соединения фаз трехфазного генератора электрической энергии
- Способы соединения фаз трехфазного генератора электрической энергии
- Соединение фаз генератора звездой
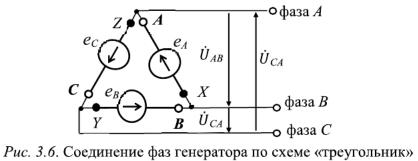
- Соединение фаз генератора треугольником
Варианты подключения обмоток трехфазных генераторов
При работе 3-х фазного генератора в каждой его обмотке создается ЭДС в форме синусоидального колебания. Все вектора разнесены по углу вращения на 120° и могут быть описаны формулами:
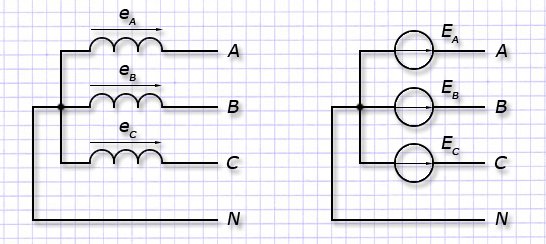
Для подключения обмоток генератора в связанную систему применяется одна из двух схем:
— “звезда” (Y); — “треугольник” (Δ).
“Звезда”. Для схемы “звезды” все выходы обмоток фаз статора подключают к единой общей точке N, именуемую нейтральной либо нулевой точкой. Входа (начала) обмоток каждой фазы А, В и С подключают к линейным выводам генератора.
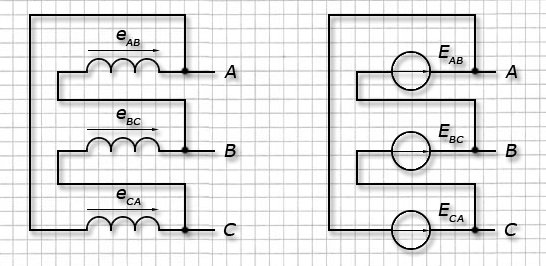
“Треугольник”. Для этой схемы соединения формируют выходные фазы:
— “А” подключением выхода обмотки А ко входу обмотки C; — “В” подключением выхода обмотки В ко входу обмотки А; — “С” подключением выхода обмотки С ко входу обмотки В.
Точки подключения А, В и С используются как линейные выводы у генератора.
Векторные диаграммы. У работающего генератора, обмотки которого соединены по схеме “звезда” диаграмма векторов напряжений имеет форму равностороннего треугольника с центром в начале координат и расположенного симметрично относительно оси ординат.
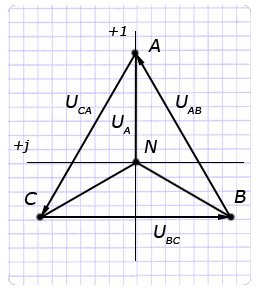
Под термином фазного напряжения понимают разность потенциалов между общим выводом N и линейным А, В или С и маркируют: UA, UB, UC. Напряжения в фазах генератора равны ЭДС обмоток: ЕА=UА, ЕВ=UВ, ЕС=UС.
Линейное напряжение генератора измеряется между двумя любыми его выводами и обозначается по наименованию выбранных фаз: UAВ, UBС, UCА. Величина вектора линейного напряжения определяется геометрической разностью векторов соответствующих фаз:
У генератора с обмотками соединенными по схеме “треугольник” диаграмма векторов напряжений тоже имеет форму равностороннего треугольника, но он относительно центра координат провернут на 30° по направлению движения часовой стрелки.

Расчеты параметров трехфазных сетей проводятся математическими способами (например, комплексный метод) и способами геометрических сложений.
Для этого выбирают один из векторов в качестве начального, ориентируют его в комплексной плоскости с учетом направления и величины. Остальные вектора достраивают по углам сдвига их фаз относительно выбранного начального вектора с учетом их величин.
Обычные расчеты для схемы соединения “звезда” проще начинать с определения напряжения вектора фазы А, который в данной системе выходит из начала координат комплексной плоскости в направлении на север. Выражения фазных напряжений в комплексной форме для такого расчета описываются формулами:
Формулы для линейных векторов имеют следующий вид:
Для схем “треугольник” за начальный отсчет принимают вектор линейного напряжения UАВ. Формулы вычисления фазных векторов напряжений принимают выражения:
Вектора линейных напряжений описываются формулами:
Проведя геометрические вычисления не сложно определить линейную величину вектора по значению фазной:
Важно! Схема соединения обмоток “треугольник” для генератора практически не пригодна для реального использования, поэтому ее запрещено применять.
В фазах схемы “треугольник” образуется общий контур, у которого возникает суммарная ЭДС Σe=eAB+eBC+eCA. Значения полных сопротивлений в обмотках маленькие и даже небольшая величина суммарной ЭДС Σe>0 вызывает в магистралях “треугольника” уравнительные токи, которые сопоставимы с номинальным значением тока в генераторе. Это создает большие потери энергии и значительно уменьшает КПД генератора.
У энергетиков существует определение номинального напряжения для 3-х фазной системы. Им называют линейные напряжения, которые выражаются в киловольтах (кВ, kV). Их представляют значениями 0,4; 1,1; 3,5; 6,3; 10,5; 22; 35; 63; 110; 220; 330; 500; 750.
Для потребителей электроэнергии номинальную величину 3-х фазного напряжения допускается указывать соотношениями линейных и фазных напряжений UЛ/UФ. Для электросети 0,4 кВ оно будет иметь вид: 380/220 вольт.
Источник
§ 3.6. Соединение обмоток генератора трехфазного тока
Соединение звездой
При соединении звездой (условное обозначение Y) концы обмоток X, Y и Z соединяются в одной точке О, которая называется нулевой точкой или нейтралью (рис. 3.15). Начала и концы обмоток определяют по правилу, о котором было рассказано в § 3.5. Разметка выводов обмоток на концы и начала — это не простая формальность.
Если при прохождении ротора через обмотку АХ в начале А обмотки и в конце X обмотки потенциалы были равны соответственно φA и φB, то после поворота ротора на 120°, т. е. при прохождении его через обмотку BY, обязательно должны выполняться равенства φB = φA и φY = φX. То же относится к началу С и концу Z третьей обмотки генератора. Генератор соединяется с потребителями тока четырьмя проводами. Три из них, присоединенные к началам А, В и С обмоток, называются линейными проводами. Провод, присоединенный к нулевой точке, называется нейтральным или нулевым проводом.
Напряжения между каждым из линейных проводов и нейтральным проводом называются фазными напряжениями. Их действующие значения обозначаются соответственно UA, UB, UC или в общем виде Uф.
Напряжения между линейными проводами называются линейными напряжениями. Их действующие значения обозначаются соответственно UAB, UBC, UCA или в общем виде UЛ.
Установим соотношение между линейными и фазными напряжениями при соединении обмоток генератора звездой. Мгновенное значение линейного напряжения UAB между фазами A и В равно разности потенциалов между началами обмоток А и В:
Таким образом, линейные напряжения равны разности соответствующих фазных напряжений.
При разомкнутом генераторе фазные напряжения uA, uB, uC равны по модулю и противоположны по знаку соответствующим ЭДС eA, eB, eC в его обмотках. Амплитуды фазных напряжений равны амплитуде ЭДС обмоток:
Вычислим линейное напряжение между фазами А и В:
Аналогичные выражения можно получить для uBC и uCA.
Отсюда видно, что при соединении обмоток генератора звездой линейные напряжения изменяются по гармоническому закону с той же чистотой, что и фазные напряжения, а амплитуда колебаний линейного напряжения больше амплитуды колебаний фазного напряжения в 

К этому же результату можно прийти, если построить векторную диаграмму для действующих значений фазных и линейных напряжений (рис. 3.16) с учетом того, что:
Соединение обмоток генератора треугольником
При соединении обмоток генератора трехфазного тока треугольником (условное обозначение Δ) конец первой обмотки X соединяется с началом второй обмотки В, конец второй обмотки У соединяется с началом третьей обмотки С и конец третьей обмотки Z — с началом первой обмотки A (рис. 3.17).
Три линейных провода, идущих к потребителям тока, присоединяются к началам обмоток (фаз) А, В, С. При таком соединении обмоток, как видно из рисунка 3.17, фазные напряжения равны линейным напряжениям:
При соединении треугольником три обмотки (фазы) генератора образуют замкнутый контур с весьма малым сопротивлением. Но полная ЭДС контура равна нулю:
Поэтому сила тока в обмотках ненагруженного генератора равна нулю.
В справедливости равенства (3.6.7) можно убедиться, сложив векторы ЭДС на векторной диаграмме (рис. 3.18).
Опасно неправильное соединение обмоток генератора треугольником, когда, например, конец первой обмотки X соединен с началом второй обмотки В, но конец второй обмотки У соединен с концом третьей обмотки Z и начало третьей обмотки С соединено с началом первой обмотки А. В этом случае результирующая ЭДС не равна нулю (предлагаем вам доказать, что она по модулю равна удвоенному значению фазной ЭДС), что при малом сопротивлении обмоток генератора равносильно короткому замыканию.
При соединении обмоток генератора треугольником для получения нужного линейного напряжения каждая фазная обмотка должна быть рассчитана на напряжение, в 
Соединение треугольником допустимо лишь при одинаковой или почти одинаковой нагрузке фаз. Иначе сила тока в замкнутом контуре обмоток окажется слишком большой, что опасно для генератора.
Источник
Способы соединения фаз трехфазного генератора электрической энергии
Способы соединения фаз трехфазного генератора электрической энергии
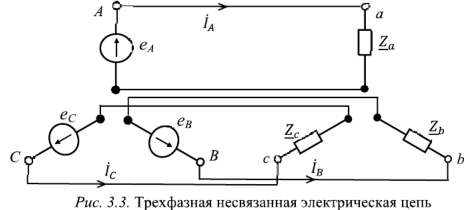
В несвязанной трехфазной системе фазы генератора электрически не связаны друг с другом (рис. 3.3). В такой системе каждая фаза генератора соединяется с приемником (нагрузкой) двумя проводниками, т.е. в этом случае требуется шесть соединительных проводников.
Для уменьшения количества соединительных проводников используют связанные трехфазные системы, в которых фазы генератора соединяются между собой звездой или треугольником.
Соединение фаз генератора звездой
При соединении фаз генератора по схеме «звезда» концы фазных обмоток 
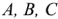
При соединении фаз генератора по схеме «звезда» образуются два уровня напряжений: фазные и линейные.
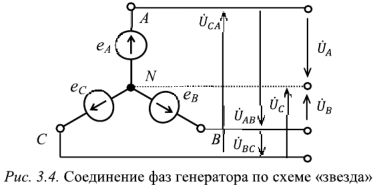
Фазным напряжением называют напряжение между началом (фазным выводом) и концом фазы генератора, т.е. напряжение каждой фазы. При соединении фаз генератора но схеме «звезда» (рис. 3.4) фазными являются напряжения между началами фаз и нейтральной точкой 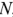
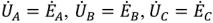
Фазные напряжения 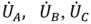
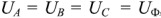
Линейные напряжения 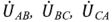
Для нахождения связи между линейными и фазными напряжениями запишем согласно с выбранными условными положительными направлениями линейных и фазных напряжений и в соответствии со вторым законом Кирхгофа уравнение для контура 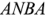
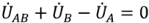
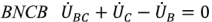
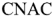
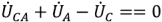
Следовательно, комплексное линейное напряжение равно разности соответствующих комплексных фазных напряжений.
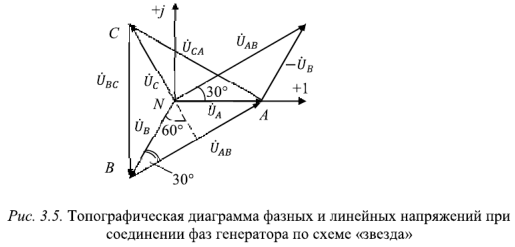
Построим топографическую диаграмму фазных и линейных напряжений при соединении фаз генератора по схеме «звезда».
Топографическая диаграмма — это векторная диаграмма, в которой определенным точкам цепи соответствуют определенные точки диаграммы. В ней вектор, соединяющий две точки, отображает напряжение между ними.
При построении топографической диаграммы (рис. 3.5) в качестве исходной (опорной) точки диаграммы возьмем нейтральную точку 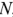
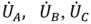
Концы этих векторов — точки 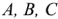
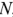
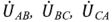
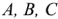
Для нахождения векторов линейных напряжений можно также непосредственно воспользоваться выражениями (3.4). Действительно, как следует из (3.4) для нахождения вектора 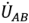
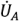
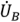
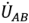
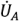
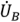
На построенной таким образом топографической диаграмме (рис.3.5) векторы линейных напряжений образуют замкнутый треугольник, из которого следует, что сумма комплексных линейных напряжений всегда равна нулю, т.е.
и действующие значения линейных напряжений у симметричного трехфазного источника 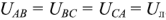
Из представленной на рис.3.5 топографической диаграммы
Таким образом, действующее значение линейного напряжения генератора, фазы которого соединены звездой, в 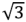
Из представленной на рис.3.5 топографической диаграммы также следует, что каждое линейное напряжение генератора опережает по фазе соответствующее ему фазное напряжение на 30°:
Соединение фаз генератора треугольником
При соединении фаз генератора треугольником конец 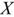
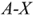
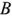
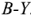
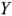
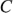
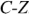
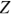
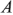
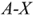
Линейные (фазные) провода образуют трехпроводную линию электропередачи и линейные напряжения тождественно равны фазным.
При симметричных обмотках 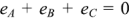
Эта теория взята со страницы помощи с заданиями по электротехнике:
Возможно эти страницы вам будут полезны:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник