Какие существуют способы решения систем уравнений с двумя переменными

Системы уравнений

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений с двумя неизвестными.

Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют « x » и « y »), которые объединены в общую систему фигурной скобкой.

Например, система уравнений может быть задана следующим образом.

x + 5y = 7

3x − 2y = 4

Чтобы решить систему уравнений, нужно найти и « x », и « y ».

Как решить систему уравнений

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки
или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений, всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

x + 5y = 7

3x − 2y = 4

Выразим из первого уравнения « x + 5y = 7 » неизвестное « x ».

Чтобы выразить неизвестное, нужно выполнить два условия:

• перенести неизвестное, которое хотим выразить, в левую часть уравнения;
• разделить и левую и правую часть уравнения на нужное число так, чтобы коэффициент при неизвестном стал равным единице.

Перенесём в первом уравнении « x + 5 y = 7 » всё что содержит « x » в левую часть, а остальное в правую часть по правилу переносу.

При « x » стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.

x = 7 − 5y

3x − 2y = 4

Теперь, вместо « x » подставим во второе уравнение полученное выражение
« x = 7 − 5y » из первого уравнения.

x = 7 − 5y

3(7 − 5y) − 2y = 4

Подставив вместо « x » выражение « (7 − 5y) » во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным « y ». Решим его по правилам решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение « 3(7 − 5y) − 2y = 4 » отдельно. Вынесем его решение отдельно с помощью обозначения звездочка (*) .

x = 7 − 5y

3(7 − 5y) − 2y = 4 (*)

Мы нашли, что « y = 1 ». Вернемся к первому уравнению « x = 7 − 5y » и вместо « y » подставим в него полученное числовое значение. Таким образом можно найти « x ». Запишем в ответ оба полученных значения.

x = 7 − 5y

y = 1

x = 7 − 5 · 1

y = 1

x = 2

y = 1

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения. Вернемся к нашей системе уравнений еще раз.

x + 5y = 7

3x − 2y = 4

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

При сложения уравнений системы левая часть первого уравнения полностью складывается с левой частью второго уравнения, а правая часть полностью складывается с правой частью.

x + 5y = 7	(x + 5y) + (3x − 2y) = 7 + 4
+ =>	x + 5y + 3x − 2y = 11
3x − 2y = 4	4x + 3y = 11

При сложении уравнений мы получили уравнение « 4x + 3y = 11 ». По сути, сложение уравнений в исходном виде нам ничего не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

x + 5y = 7

3x − 2y = 4

Чтобы при сложении неизвестное « x » взаимноуничтожилось, нужно сделать так, чтобы в первом уравнении при « x » стоял коэффициент « −3 ».

Для этого умножим первое уравнение на « −3 ».

При умножении уравнения на число, на это число умножается каждый член уравнения.

x + 5y = 7 | ·(−3)

3x − 2y = 4

x · (−3) + 5y · (−3) = 7 · (−3)

3x − 2y = 4

−3x −15y = −21

3x − 2y = 4

Теперь сложим уравнения.

−3x −15y = −21	(−3x −15y ) + (3x − 2y) = −21 + 4
+ =>	− 3x − 15y + 3x − 2y = −21 + 4
3x − 2y = 4	−17y = −17 |:(−17)
y = 1

Мы нашли « y = 1 ». Вернемся к первому уравнению и подставим вместо « y » полученное числовое значение и найдем « x ».

x = 7 − 5y

y = 1

x = 7 − 5 · 1

y = 1

x = 2

y = 1

Ответ: x = 2; y = 1

Пример решения системы уравнения
способом подстановки

Выразим из первого уравнения « x ».

x = 17 + 3y

x − 2y = −13

Подставим вместо « x » во второе уравнение полученное выражение.

x = 17 + 3y

(17 + 3y) − 2y = −13 (*)

Подставим в первое уравнение полученное числовое значение « y = −30 » и найдем « x ».

x = 17 + 3y

y = −30

x = 17 + 3 · (−30)

y = −30

x = 17 −90

y = −30

x = −73

y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения
способом сложения

Рассмотрим систему уравнений.

3(x − y) + 5x = 2(3x − 2)

4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

3x − 3y + 5x = 6x − 4

4x − 2x − 2y = 4 − 3y

8x − 3y = 6x − 4

2x −2y = 4 − 3y

8x − 3y − 6x = −4

2x −2y + 3y = 4

2x − 3y = −4

2x + y = 4

Мы видим, что в обоих уравнениях есть « 2x ». Наша задача, чтобы при сложении уравнений « 2x » взаимноуничтожились и в полученном уравнении осталось только « y ».

Для этого достаточно умножить первое уравнение на « −1 ».

2x − 3y = −4 | ·(−1)

2x + y = 4

2x · (−1) − 3y · (−1) = −4 · (−1)

2x + y = 4

−2x + 3y = 4

2x + y = 4

Теперь при сложении уравнений у нас останется только « y » в уравнении.

−2x + 3y = 4	(−2x + 3y ) + (2x + y) = 4 + 4
+ =>	− 2x + 3y + 2x + y = 4 + 4
2x + y = 4	4y = 8 | :4
y = 2

Подставим в первое уравнение полученное числовое значение « y = 2 » и найдем « x ».

Источник

Методы решения систем уравнений с двумя переменными

п.1. Метод подстановки

Вариант 1
Шаг 1. Из одного уравнения выразить y через x: y(x).
Шаг 2. Подставить полученное выражение во второе уравнение и найти x.
Шаг 3. Подставить найденный x в y(x) и найти y.
Шаг 4. Записать полученные пары решений. Работа завершена.

Вариант 2
Шаг 1. Из одного уравнения выразить x через y: x(y).
Шаг 2. Подставить полученное выражение во второе уравнение и найти y.
Шаг 3. Подставить найденный y в x(y) и найти x.
Шаг 4. Записать полученные пары решений. Работа завершена.

п.2. Метод сложения

п.3. Метод замены переменных

Иногда удобно ввести новые переменные и решить систему для них.
А затем, вернуться к исходным переменным и найти их значения.

п.4. Графический метод

Графический метод подробно рассмотрен в §15 данного справочника.

п.5. Примеры

Пример 1. Решите систему уравнений:
а) \( \left\< \begin < l >\mathrm & \\ \mathrm & \end\right. \)
Решаем методом подстановки: \( \left\< \begin < l >\mathrm & \\ \mathrm & \end\right. \)
Для нижнего уравнения: \( \mathrm \)
Подставляем в верхнее уравнение: \( \mathrm \)

б) \( \left\< \begin < l >\mathrm & \\ \mathrm <(x^2+y^2)xy=10>& \end\right. \)
Замена переменных: \( \left\< \begin < l >\mathrm & \\ \mathrm & \end\right. \)
Выразим (x 2 + y 2 ) через a и b:
x 2 + y 2 = (x 2 + y 2 + 2xy) – 2xy = (x + y) 2 – 2xy = a 2 – 2b
Подставляем: \( \left\< \begin < l >\mathrm & \\ \mathrm <(a^2-2b)b=10>& \end\right.\Rightarrow \left\< \begin < l >\mathrm & \\ \mathrm <9b-2b^2=10>& \end\right. \)
Решаем нижнее уравнение: 2b 2 – 9b + 10 = 0 $$ \mathrm< D=9^2-4\cdot 2\cdot 10=1,\ \ b=\frac<9\pm 1><4>> = \left[\begin < l >\mathrm & \\ \mathrm & \end\right. $$ Возвращаемся к исходным переменным: \( \left[\begin < l >\left\<\begin < l >\mathrm & \\ \mathrm & \end\right.& \\ \left\<\begin < l >\mathrm & \\ \mathrm & \end\right. \end\right. \)

Источник

Системы уравнений с двумя переменными, способы решения

Вы будете перенаправлены на Автор24

Напомним для начала определение решения системы уравнений с двумя переменными.

Пара чисел называется решением системы уравнений с двумя переменными, если при их подстановки в уравнение получается верное равенство.

В дальнейшем будем рассматривать системы из двух уравнений с двумя переменными.

Существуют четыре основных способа решения систем уравнений: способ подстановки, способ сложения, графический способ, способ ведения новых переменных. Рассмотрим эти способы на конкретных примерах. Для описания принципа использования первых трех способов будем рассматривать систему двух линейных уравнений с двумя неизвестными:

Способ подстановки

Способ подстановки заключается в следующем: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$

Выразим из второго уравнения $y$ через $x$:

Подставим в первое уравнение, найдем $x$:

Ответ: $(-2,\ 3)$

Способ сложения.

Рассмотрим данный способ на примере:

Умножим второе уравнение на 3, получим:

Теперь сложим оба уравнения между собой:

Найдем $y$ из второго уравнения:

Ответ: $(-2,\ 3)$

. Отметим, что в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении одна из переменных «исчезла».

Готовые работы на аналогичную тему

Графический способ

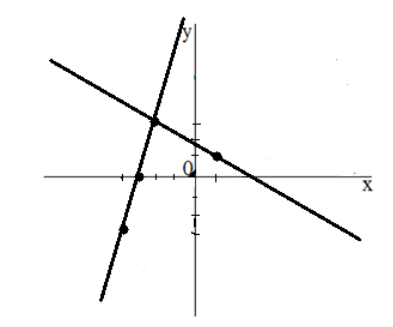
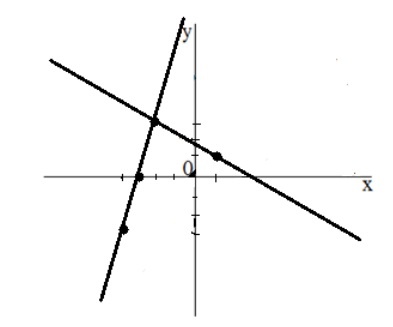
Графический способ заключается в следующем: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.

Выразим из обоих уравнений $y$ через $x$:

Изобразим оба графика на одной плоскости:

Ответ: $(-2,\ 3)$

Способ введения новых переменных

Этот способ рассмотрим на следующем примере:

Решение.

Данная система равносильна системе

Пусть $2^x=u\ (u>0)$, а $3^y=v\ (v>0)$, получим:

Решим полученную систему методом сложения. Сложим уравнения:

Тогда из второго уравнения, получим, что

Возвращаясь к замене, получим новую систему показательных уравнений:

Источник

Решение систем уравнений с двумя переменными

Что такое система уравнений с двумя переменными

Система уравнений с двумя переменными — это два уравнения, которые рассматриваются вместе и отличаются наличием одинаковых неизвестных.

При нахождении неизвестных и подстановке их значений, уравнения становятся истинными равенствами.

Способы решения

Такие уравнения можно решить:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

• подстановкой;
• домножением и сложением;
• построением графиков;
• введением новых переменных.

Способ подстановки

Известна одна переменная, а нужно найти вторую. Для этого необходимо подставить известную переменную в одно из уравнений системы. Суть в том, что раз это система, то в обоих уравнениях имеются в виду одни и те же переменные. Получится простое линейное уравнение. Решив его, можно узнать значение второй переменной.

Пример 1

Известно, что z=2. Тогда можно найти t, подставив значение z в уравнение номер 2.

В случае подстановки известного значения z=2 в уравнение номер 1 результат будет такой же:

С более сложными уравнениями, когда изначально ни для одной переменной точного значения не дано, этот метод работает точно так же.

Пример 2

Не установлены значения ни для p, ни для c. Поэтому нужно воспользоваться первым уравнением и выразить переменную c из него:

Теперь значение одной из переменных известно. Далее, пользуясь стандартным алгоритмом из примера 1, нужно подставить полученное значение c во второе уравнение.

Теперь надо его решить:

Это равенство неверное, потому что не существует таких значений для p и с, чтобы 4=6.

Ответ: решений нет.

Способ сложения

Если даны два верных равенства в системе уравнений, то можно складывать их правые и левые части, и равенство получится тоже верным.

В системе линейных уравнений складывать нужно левые и правые части каждого из них. Для того, чтобы избавиться, если это возможно, от одной из переменных. Цель — прийти к простому уравнению с одной переменной, которое не требует сложного решения.

Пошаговое решение

1. Надо сложить отдельно правую часть первого уравнения с правой частью второго, а левую — с левой.

2. Произвести необходимые вычисления (привести подобные в левой части и произвести сложение в правой) и найти значение одной из переменных. Получится:

3. Подставить полученное значение n в одно из уравнений системы (в любое), чтобы найти значение второй переменной. Выберем, например, уравнение номер 1:

Замечание при решении уравнения

В примере выше изначально были даны уравнения с одинаковыми по модулю коэффициентами слагаемых (−5m и 5m). Такое явление нельзя назвать частым. Поэтому необходим навык приведения любых уравнений системы к такому виду. Для этого нужно научить способу домножения обеих частей уравнения на одно и тоже число, не равное нулю.

Пример

В уравнении номер 2 видим переменную с числовым коэффициентом −18. А в первом ту же переменную с коэффициентом 9. Нам нужно сделать так, чтобы эта переменная убралась. Для этого нужно из 9 сделать 18. Возьмем уравнение номер 1. Произведем умножение обеих его частей на 2. Получим:

Теперь в обоих уравнениях есть одинаковые слагаемые, которые можно сократить. Для этого выполним метод сложения соответствующих частей обоих уравнений друг с другом.

Теперь можно поставить полученное значение v в первое (или в любое) уравнение, чтобы найти t:

Графический способ

Суть способа в том, чтобы изобразить оба данных уравнения с помощью системы координат и произвести поиск точек пересечения их графиков.

Системные уравнения имеют графики в виде прямых:

• пересекающиеся означают, что решение только одно;
• параллельные — что решений нет;
• совпадающие — что решений множество.

Как нарисовать графики уравнений

Пример

1. Сначала нужно выразить из каждого уравнения переменную y через x для получения функции:

Выражаем именно y, потому что графики в большинстве случаев принято строить относительно x.

2. Затем приступаем к самому процессу построения графиков получившихся функций. Для этого нужно найти координаты всего лишь двух точек для каждой функции. Нужно взять любое значение x и подставить его сначала в первое уравнение, чтобы получить его координаты. Затем то же самое проделать со вторым для нахождения его координат:

• для первого уравнения, если x=1, то y=1;
• для второго уравнения, если x=−4, то y=−3.

Чертим графики, используя получившиеся точки. Получаются две прямые.

3. Находим точку пересечения графиков: она имеет координаты (−2;3). Это и будет решением данной системы уравнений.

Точка пересечения

Это понятие обозначает место, где два графика пересекают друг друга. Такая точка в системе линейных уравнений может быть только одна. Нахождение точки пересечения графиков функций, полученных при выражении y из уравнений системы — это и есть графическое решение любой системы уравнений. Это хорошо показано на примере в предыдущем подпункте (п.3).

Способ введения новых переменных

Это свойство систем уравнений имеет целью упрощение этих систем для более быстрого решения.

Существует два варианта подобного пути:

• введение одной новой переменной и только в одном уравнении системы;
• введение двух новых переменных в обоих уравнениях в одно и то же время.

Как вводить новую переменную

Новая переменная\ые вводятся вместо повторяющихся в уравнении сочетаний, заменяют их и тем самым упрощают всю систему. В результате замены получается два простых линейных уравнения, которые легко решаются.

Пример 1

Вводим 2 новые переменные: вместо mn будет t, а вместо m+n поставим z. Это поможет упростить систему, получится:

Далее легко найти значения переменных в получившихся уравнениях:

Далее нужно просто подставить эти значения вместо тех, которые заменяли введенные переменные, и дорешать получившиеся уравнения.

Пример 2

Вводим новые переменные:

заменим на t, а вместо

поставим z. Теперь система примет такой вид:

Далее по методу сложения вычтем второе уравнение из первого. Получим:

Источник