Какие существуют способы определения площадей

Cпособы определения площадей в геодезии

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра.

В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют различные способы определения площадей.

1. Аналитический, когда площадь вычисляется по результатам измерений линий на местности, по результатам измерений линий и углов на местности или по их функциям (координатам вершин фигур).

2. Графический, когда площадь вычисляется по результатам измерений линий или координат на плане (карте). Графические способы. Участок на плане разбивают на простые геометрические фигуры (обычно – треугольники), элементы которых измеряют с помощью измерителя и поперечного масштаба, а площади вычисляют по известным формулам и суммируют.

3. Механический, когда площадь определяется по плану с помощью специальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применяют комбинированно, например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности.

Площади можно также определить на ЭВМ по цифровой модели местности по специальной программе.

При аналитическом способе определения площадей применяются формулы геометрии, тригонометрии и аналитической геометрии. При определении площадей небольших участков (для учета площадей, занятых строениями, усадьбами, площадей вспашки, посева) участки разбиваются на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции. В этом случае площади участков определяются как суммы площадей отдельных фигур, вычисляемых по линейным элементам — высотам и основаниям.

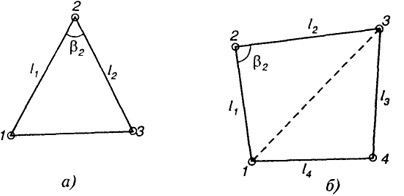
Рис. 23.1. Геометрические фигуры для определения площадей участков (а, б)

Если по границам участка выполнены геодезические измерения, то площадь всего участка или его части можно вычислить по формулам, приведенным применительно к следующим фигурам участков (рис. 23.1).

Треугольник (рис. 23.1, а). Площадь треугольника определяется по сторонам l₁ и l₂, углу β₂, заключенному между ними, по формуле

Четырехугольник (рис. 23.1, б). В зависимости от элементов, известных в четырехугольнике, могут быть использованы различные формулы для расчета, в связи с чем приведем пример, характеризующий это многообразие. Пусть в четырехугольнике измерены все стороны и один угол при вершине 2. В таком случае площадь треугольника 1 — 2 — 3 может быть вычислена по формуле (23.1). При этом полезно вычислить длину l_1-3, используя теорему косинусов

Площадь треугольника 1 — 3 — 4 может быть вычислена по формуле

где S — полупериметр, равный

Общая площадь четырехугольника будет равна:

Источник

Способы определения площадей земельных участков

ГОУ ВПО «Дальневосточный государственный университет

Кафедра «Изыскания и проектирование железных дорог»

СПОСОБЫ ОПРЕДЕЛЕНИЯ ПЛОЩАДЕЙ

ЗЕМЕЛЬНЫХ УЧАСТКОВ

Методические указания по выполнению

УКД 528.48.068.03: 625

А 674

, . Способы определения площадей земельных участков. Методические указания по выполнению лабораторной работы. – Хабаровск: ДВГУПС, 2010. – 18 с.

Методические указания соответствуют требованиям ГОС ВПО по направлениям подготовки дипломированного специалиста 653600 «Транспортное строительство» и 653500 «Строительство».

Указания разработаны в соответствии с программой курса инженерной геодезии для строительных специальностей и предназначено студентам всех форм обучения, изучающих дисциплину ‘‘Инженерная геодезия’’.

В методических указаниях изложена методика выполнения лабораторной работы по способам определения площадей, приведены примеры вычислений и образцы оформления работы.

А 674

Ó ГОУ ВПО  «Дальневосточный государственный университет путей сообщения» (ДВГУПС), 2010

Изучение «Инженерной геодезии» складывается из лекционных, лабораторных, практических работ и полевой практики. Использованию методического указания должно предшествовать изучение соответствующих разделов учебника. Это требование должно обязательно выполняться студентами.

Наличие в методическом указании краткого описания основных понятий и формул для вычислений обусловлено необходимостью обратить внимание студентов на существо вопроса перед переходом к закреплению материала путем выполнения лабораторной работы. Выполнение лабораторной работы рассчитано на два часа занятий.

Настоящее методическое указание к лабораторной работе имеет своей целью дать студентам первого курса строительных специальностей знания по методам и приемам определения площадей с учётом погрешностей всех геодезических измерений. В методическом указании приведены методы и приемы определения площадей, рассмотрены вопросы точности определения площадей с учетом погрешностей всех геодезических измерений.

Для закрепления теоретических знаний и практических навыков в методическом указании приведены контрольные вопросы для самоконтроля.

1. ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ

Составление различного рода проектов, связанных с использованием земельной территории, изучение её природных богатств, учет и инвентаризация земель требует определения площадей. При проведении этих работ определяются площади небольших участков или больших земельных массивов, суммы площадей нескольких несмежных участков, обладающих одними и теми же природными или хозяйственными признаками.

К таким площадям могут относиться различные сельскохозяйственные территории (луга, пашни, огороды), лесонасаждения, площади под планировку и застройку. А также территории осушения (болота), площади бассейнов водотоков (рек и оврагов), границы затоплений, водные пространства (озера, пруды, водохранилища), площади насыпей и выемок для подсчета объемов земляных дорог и других сооружений [3].

В одних случаях достаточно ограничиться общими сведениями о площади участков и массивов, а в других случаях необходимы более точные способы определения площадей и погрешность даже в несколько десятых долей процента считается недопустимой. Поэтому наряду с определением площади очень часто требуется знать и точность её определения. При определении площадей по результатам измерений на местности точность зависит от качества этих измерений, в то время как при измерении площади по плану (или карте) на точность площади влияет качество измерений на местности, по которым составляется план или карта, графических построений участка на плане и определения площади по плану.

В зависимости от хозяйственной значимости участков и массивов, их размеров, конфигурации и вытянутости, наличия планово – топографического материала, топографических условий местности применяют следующие способы определения площадей:

1. Аналитический способ — когда площадь вычисляется по результатам измерений линий на местности или по их функциям (координатам вершин участка);

2. Графический способ — когда площадь вычисляется по результатам измерений линий на плане (карте);

3. Механический способ — когда площадь определяется по плану при помощи специальных приборов (планиметров).

Иногда эти способы применяются комбинированно. Например, общая площадь определяется аналитическим способом (по координатам вершин), а площади внутренних контуров – графическим или механическим способом. Далее в методическом указании будет более подробно рассмотрен каждый из выше перечисленных способов определения площадей.

1.1 Аналитический способ определения площадей

Цель: ознакомиться и получить навык определения площадей аналитическим способом.

Вычисление площади этим способом производится по формулам геометрии, тригонометрии и аналитической геометрии. Исходными данными для вычисления служат измеренные в натуре углы или их функции – координаты.

Если участок представляет собой простейшую геометрическую фигуру (треугольник, трапецию и др.), то площадь его вычисляют по общеизвестным формулам геометрии или тригонометрии [4,5]. Площади многоугольников вычисляют обычно по координатам вершин (рис. 1).

Рис. 1. Вычисление площади многоугольника по координатам.

Площадь замкнутого контура () в этом случае определяется по формулам [5]:

, (1)

(2)

где i — это порядковый номер вершин контура от 1 до n; n — число вершин полигона; x, y — координаты вершин контура.

При подстановке i = 1 получим в первой формуле x0 — x2, а второй y2 — y0, где вместо x0 и y0 необходимо подставить xn и yn; если при подстановке i = n получим в первой формуле xn-1 — xn+1, во второй yn+1 — yn-1, где вместо xn+1, yn+1 необходимо подставить x1 и y1 (так как нулевая точка предшествует первой, а в данном случае первой вершине предшествует вершина n; точка n + 1 следует за точкой n, а в данном случае за вершиной n следует первая вершина) [4,5]. Вычисление площади производиться для контроля по обеим формулам.

В таблице 1 приведен пример расчета площади при помощи аналитического способа. В соответствие с рисунком 1 в графах 1 и 2 таблицы 1 заданы прямоугольные координаты каждой вершины замкнутого полигона.

Разности координат xi-1 — xi+1 и yi+1 – yi-1 с соответствующим знаком запишем в графы 3 и 4. Например, для вершины 1 разность будет складываться из координаты последующей вершины 2 (Х2 = 209,43) и координаты предыдущей вершины 6 (Х6 = 209,43). Результат перемножения соответственно граф 2 и 3, а также 1 и 4 запишем в графы 5 и 6.

Таким образом, площадь участка составляет 0998 м2 или 14,1 га. Вычисление разностей координат контролируется тем, что алгебраическая сумма, как разностей координат X, так и разностей координат Y должна равняться нулю, либо при составлении разностей каждая координата входит как со знаком плюс, так и со знаком минус. Совпадение сумм произведений в обоих случаях указывает на отсутствие ошибок вычислений.

Сумма произведений соответствует удвоенной площади полигона в квадратных метрах, так как координаты даны в метрах.

Точность аналитического способа 1/1000. При определении площади этим способом на точность влияют только погрешности измерений на местности.

Источник

Способы определения площадей. Точность определения площадей различными способами.

В зависимости от хозяйственного назначения участков и контуров, их размеров, формы, наличия или отсутствия планов и карт площади определяют след. методами.

Аналитический способ. Площади вычисляют по результатам измерений линий и углов на местности с применением формул геометрии, тригонометрии и аналитической геометрии. Например при учете площадей, занятых строениями усадьбами, пашней, посевами, при отводе мелких участков их разбивают на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции и площади участков определяют как суммы площадей отдельных фигур, вычисляемых по формулам геометрии. При учете площадь пашни, посевов, уборки урожая определяют по длине маршрута агрегата и ширине его захвата.

Площади больших участков, целых землепользований вычисляют по результатам измерений линий и углов на местности (при помощи формул тригонометрии) или по их функциям – приращениям координат и координатам вершин полигона.

Формула для любого n-угольника выглядит так

Т.е. удвоенная площадь полигона равна сумме произведений каждой абсциссы на разность ординат последующей и предыдущей точек.

Перед вычислением площади значения координат можно округлять до 0,1 м, а если площадь полигона более 200 га, то до 1 м, это округление упрощает вычисления без заметного снижения точности.

Графический способ. Площади вычисляют по результатам измерений линий по плану (карте), когда участок, изображенный на плане, разбивают на простейшие геометрические фигуры, преимущественно на треугольники, реже на прямоугольники и трапеции. В каждой фигуре на плане измеряют высоту и основание, по которым вычисляют площадь. Сумма площадей фигур дает площадь участка. К графическому способу относят определение площади при помощи палеток.

Для определения на плане площадей небольших участков с криволинейными контурами применяют прямолинейные и криволинейные палетки. К прямолинейным относят известные и наиболее распространенные квадратные и параллельные палетки.

Квадратная палетка представляет сеть взаимно перпендикулярных линий, проведенных через 1 мм на прозрачном целлулоиде, фотопленке, стекле или восковке. Площадь фигуры вычисляют простым подсчетом клеток палетки, наложенной на фигуру. Доли клеток, рассекаемых контуром на части, учитывают на глаз. Для упрощения подсчетов проводят утолщенные линии через 0,5 и 1 см, чтобы число клеток можно подсчитать сразу группами (25 и 100 мм )

Квадратной палеткой не рекомендуют определять площади, большие 2 см на плане.

Недостаток ее применения помимо того, что площади долей клеток, рассекаемых контуром, приходится оценивать на глаз, состоит еще в том, что подсчет числа целых клеток нередко сопровождается грубыми ошибками.

Таких недостатков не наблюдается при определении при определении площадей параллельной палеткой, представляющей собой листок прозрачного целлулоида или восковки, на котором нанесены параллельные линии, проведенные преимущественно через 2 мм одна от другой.

Площадь контура этой палеткой вычисляют следующим образом. Накладывают ее па контур так, чтобы крайние точки контура разместились посередине между параллельными линиями палетки. Таким образом, весь контур оказывается расчлененным параллельными линиями на фигуры, близкие к трапециям с одинаковыми высотами, причем отрезки параллельных линий внутри контура являются средними линиями трапеций. Следовательно, чтобы получить площадь контура, нужно взять сумму средних линий, т. е. сумму отрезков параллельных прямых, проходящих внутри контура, и умножить на расстояние между ними.

Источник