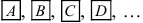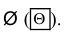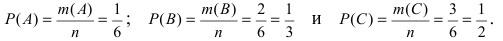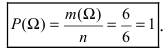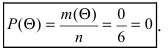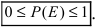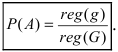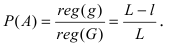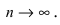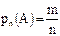Какие способы задания вероятностей вы знаете

Определения вероятности событий — вычисление с примерами решения

Содержание:

Основные понятия теории вероятностей:

1. Предмет теории вероятностей.

Теория вероятностей — это математическая дисциплина, которая устанавливает взаимозависимость между случайными величинами в случайных массовых процессах. Одним из основных понятий в теории вероятностей является понятие случайного события.

Определение: Случайным событием называется событие, которое в результате проведения эксперимента может произойти или не произойти.

Например, при подбрасывании монеты нельзя угадать заранее, что выпадет: “решка” (аверс) или “орел” (реверс). Каждое из этих событий является простым и не может быть выражено через более простые события.

Определение: Элементарным событием называется событие, которое в результате проведения эксперимента может произойти или не произойти, а также не может быть представлено посредством более простых событий.

В теории вероятностей случайные элементарные события принято обозначать заглавными начальными буквами латинского алфавита

Определение: Сложным случайным событием называется событие, которое состоит из осуществления двух или более элементарных событий.

Определение: Эксперимент — это создание заранее заданного комплекса условий. Например, при подбрасывании монеты создают следующие условия: стол, на который падает монета, должен быть ровным, гладким, достаточно большим по площади, чтобы монета не могла скатиться.

Определение: Достоверным событием называется такое событие, которое обязательно произойдет в рамках данного опыта. Достоверное событие обозначается

Определение: Невозможным событием называется такое событие, которое ни при каких условиях не может произойти.

Невозможное событие обозначается

Например, совокупность выигрыша, проигрыша и ничья в шахматной партии образуют достоверное совокупное событие, т.е. одно из этих событий обязательно произойдет при игре в шахматы. При бросании кубика выпадение грани с 7 очками является невозможным событием.

Определение: Совместными событиями называются события, которые могут одновременно произойти в рамках данного опыта, все другие события называются несовместными.

Например, при бросании кубика выпадение грани с 4 очками (событие А) и выпадение четной грани (событие В) являются совместными событиями, а выпадение грани с 3 очками (событие А) и выпадение четной грани (событие В) являются несовместными событиями.

Определение: Полной группой случайных событий называется совокупность таких несовместных событий, что в результате проведения эксперимента хотя бы одно из них обязательно произойдет.

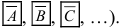
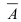
Определение: Противоположными событиями называются такие несовместные события, которые образуют полную группу (обозначаются Например, если событие А состоит в попадании снаряда в цель, то событие состоит в том, что снаряд не попадет в цель.

Замечание: Если в словесном описании случайного события присутствуют слова “хотя бы один”, то такое событие противоположно событию, содержащему в своем словесном описании слова “ни один”.

Определение: Равновозможными событиями называются такие случайные события, которые в условиях эксперимента имеют объективно равные шансы не произойти или произойти.

Например, однородность материала кости и несмещенность центра тяжести кубика являются теми условиями, при которых объективно возможно выпадение любой грани кубика.

Способы определения вероятности событий

Существуют два способа определения вероятности события

1. Теоретический способ основан на непосредственном (без проведения специального эксперимента) определении вероятности события по формуле: P(A)=m/n.
2. Статистический способ основан на предварительном прове­дении большого числа испытаний. При этом подсчитывают вероят­ность по формуле: h (A) = k / L.

Классическое определение вероятности

Определение: Вероятностью события называется численная мера степени объективной возможности случайного события.

Классическое определение вероятности применяется для нахождения вероятности конечного числа несовместных и равновозможных событии, образующих полную группу.

Пример №1

Пусть в урне находится 6 шаров: 1 белый, 2 красных и 3 синих. Опыт состоит в том, что из урны наудачу извлекают один шар. Определить полную группу случайных событий и наиболее вероятное событие.

Решение:

Для данного опыта полная группа событий состоит из 6 равновозможных исходов. Обозначим через А событие, состоящее в том, что из урны извлекают белый шар; В — красный шар; С — синий шар. Очевидно, событие С является более объективно возможным событием, чем события А и В, так как синих шаров в урне больше, чем белых и красных.

Классическое определение вероятности состоит в следующем:

Определение: Вероятностью случайного элементарного события называется отношение числа элементарных исходов, благоприятствующих появлению этого события, к общему числу всех равновозможных, несовместных, элементарных исходов, образующих полную группу.

В Примере число исходов, благоприятствующих извлечению белого шара, равно m(А) = 1, красного шара — m(В) = 2 и синего шара — m(С) = 3. Общее число всех равновозможных, несовместных, элементарных исходов, образующих полную группу, равно числу шаров в урне, т.е. n = 6. Таким образом, вероятности извлечь из урны тот или иной шар равны отношению числа элементарных исходов, благоприятствующих появлению этого события, к общему числу всех равновозможных, несовместных, элементарных исходов, образующих полную группу:

В силу того,что события А, В и С образуют достоверное совокупное событие, то 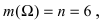следовательно, вероятность достоверного события равна:

Если в рассматриваемом Примере. обозначить через D событие, состоящее в том, что из урны извлекают черный шар, то этому событию благоприятствует нуль исходов (m(D) = 0), так как в урне нет черных шаров. Следовательно, событие D является невозможным событием О, а его вероятность равна:

Из рассмотренного Примере. видно, что вероятности всех событий есть положительные величины, которые принимают значения между вероятностью невозможного (0) и вероятностью достоверного (1) событий, т.е.

Замечание: Вероятность любого случайного события есть безразмерная и положительная величина, принимающая значения из промежутка от 0 до 1. Чем ближе вероятность события к нулю, тем меньше его возможность появления в данном опыте. Чем ближе вероятность события к единице, тем выше его возможность появления в данном эксперименте.

Геометрический способ определения вероятности

Геометрическое определение вероятности применяется для вычисления вероятности бесконечного числа несовместных и равновозможных событий, образующих полную группу.

Пусть имеется некоторая область G, которая может быть представлена в виде линии, площади или объема. Внутри области G находится другая область g, внутрь которой должна попасть точка, наудачу брошенная в область G. Пусть событие А состоит в том, что при попадании в область g включается лампочка, а при попадании в область G лампочка не загорается. Обозначим размеры областей g и G через 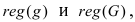соответственно. Появлению события А благоприятствует размер области g, а размер области G определяет общее число возможных исходов, следовательно, вероятность появления события А равна

Пример №2

Пусть на нити длиной L подвешен груз. Определить вероятность разрыва нити в любой точке, отстоящей от точки подвеса не менее чем на расстоянии l.

Решение:

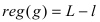
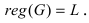
Пусть событие А состоит в том, что нить разорвется в любой точке, отстоящей от точки подвеса не менее чем на расстоянии l. Появлению этого события благоприятствуют все точки нити длиной L-l, т.е. , а длина всей нити равна L, т.е. Согласно геометрическому определению вероятности вероятность появления события А равна

Статистический способ определения вероятности событий

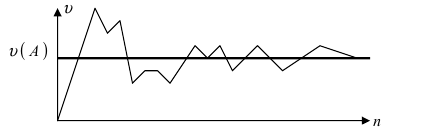
Данный способ определения вероятности событий применяется тогда, когда неприменимы два вышеприведенных способа. В основу данного способа положена устойчивость частоты появления изучаемого события при достаточно большом числе проводимых опытов, т.е. P(A) = v(A). При небольшом числе испытаний частота носит случайный характер, но при 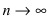она стабилизируется возле некоторого положения, характеризующего связь между комплексом условий и наблюдаемым событием (Рис. 1).

Рис. 1. Стабилизация частоты появления случайного события при

Косвенный способ определения вероятности событий

Данный способ определения вероятности событий применяется тогда, когда неприменимы три вышеприведенных способа. Он основан на теоремах теории вероятностей, которые рассматриваются ниже.

Рекомендую подробно изучить предметы:

Теория вероятностей Математическая статистика

Ещё лекции с примерами решения и объяснением:

• Предельные теоремы теории вероятностей
• Точечные оценки, свойства оценок
• Доверительный интервал для вероятности события
• Проверка гипотезы о равенстве вероятностей
• Многомерные случайные величины
• Случайные события — определение и вычисление
• Системы случайных величин
• Вероятность и риск

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Способы задания вероятностей.

1.Аксиоматический способ задания вероятностей.

Рассмотрим эксперимент, с конечным или счетным числом возможных исходов W=1, w₂, w_i… >. Предположим, что каждому элементарному событию w_i приписан некоторый »вес» p_i, называемый вероятностью появления элементарного события w_i , и потребуем, чтобы вероятность p_i удовлетворяла следующим условием:

2) ; — нормированость.

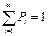
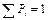
Для данного эксперимента построена вероятностная модель, если указано пространство элементарных событий W : ; и известна вероятность элементарного события Р(w_i), Р_i³ 0; ,w_iÎW.

Пусть А – произвольное случайное событие, наблюдаемое в данном эксперименте т.е. А Ì W . Тогда имеет место следующее определение.

Определение: Вероятностью события А называют сумму вероятностей элементарных событий, составляющих событие А:

.

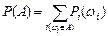
Из определения вероятности события P(A) вытекают следующие свойства вероятности:

0£P(A); — аксиома неотрицательности;

P(W)=1; — аксиома нормировки;

Аксиома адитивности (сложения):

Если А иВ несовместные события (А Ì W , В Ì W ,А·В= Æ), то Р(А+В)=Р(А)+Р(В).

Эти аксиомы были сформулированы А.Н.Колмогоровым и оказали огромное влияние на развитие теории вероятностей..Такое задание вероятности события называются аксиоматическим.

Аксиома аддитивности может быть расширена на случай n попарно несовместимых событий, т.е.

, A_iÎW ; A_i·A_j=Æ; i,j= , i¹j.

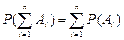
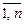
Вероятность суммы несовместимых событий равна сумме вероятностей этих событий.

Аксиому сложения вероятностей иногда называют теоремой сложения вероятностей, или правилом сложения вероятностей.

Если имеется счетное множество несовместимых событий А₁,А₂…Аn… (A_i·A_j=Æ; i¹j) то ;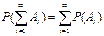

Следствия из аксиом теории вероятностей:

Следствие 1: Если А Ì В, (влечении В), то Р(А)

2. Класический способ задания вероятностей.

Если элементарное событие wi равнозначны, т.е. Р(wi)=Р, (wi имеют одинаковый вес) и А=i1,w_i2,…,w_im>, iÎI, W=1,w₂,…,w_n>, то Р(W)= ;

тогда Р(w_i)=Р·1/n; и Р(А)= .

При классическом подходе к определению вероятности вероятность события А можно трактовать как отношение исходов (элементарных событий) благоприятствующих появлению события А к общему числу равнозначных исходов. Классическое определение вероятностейоправдано тогда, когда на основании симметрии, однородности и т.п. можно говорить о равнозначных исходах или равнозначных событиях.

3. Статистическая вероятность

Наряду с классическим определением вероятности , которое базируется на понятии «равнозначности события» и применимо к конечному числу элементарных событий, используется понятие статистической вероятности. В качестве статистической вероятности принимают частоту появления события А при проведении многократных испытаниях. Пусть в результате n (n>>1) испытаний событие А появилось m раз, тогда статистическая вероятность

и получаем свойства:

, , , .

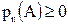
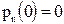
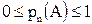
Английский математик Пирсон бросал монету 24000 раз. «Герб» выпадал 12012 раз, а значит статистическая вероятность выпадения «герба» (событие А) была равной

.

Недостаток этого определения при всей его привлекательности заключается в неоднозначности этого определения, т.е. в зависимости вероятности от числа испытаний. Другой статистический подход в определении вероятности заключается в том , что в качестве вероятности берут предел частоты появления события А при неограниченном числе испытаний:

.

Однако такой подход трудно реализовать на практике, так как невозможно произвести бесконечное число испытаний.

4. Геометрическая вероятность.

Если число равновозможных элементарных событий бесконечно, то использовать классическое определение вероятности невозможно. Однако, в таких ситуациях иногда можно воспользоваться методом геометрической вероятности. Суть метода заключается в случайном бросании точки на ограниченый участок либо прямой, либо плоскости, либо пространство. Если брошенная точка обязательно попадет в неограниченную область W , содержащую область А (А Ì W ), и вероятность попадания в любую часть W не зависит от формы этой части и пропорциональна её мере (длине, площади, объему), то вероятность попадания точки в область А равна отношению мер областей А и W :

.

Источник