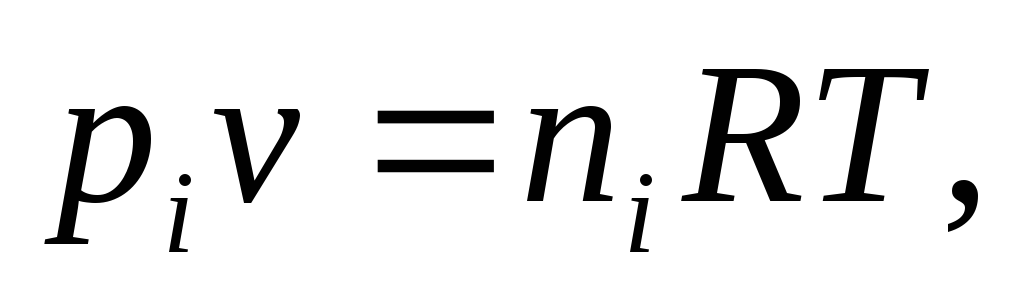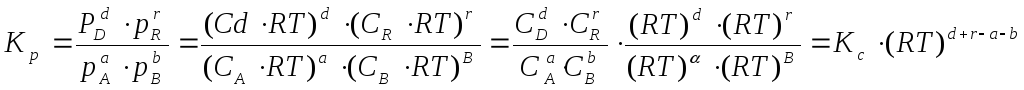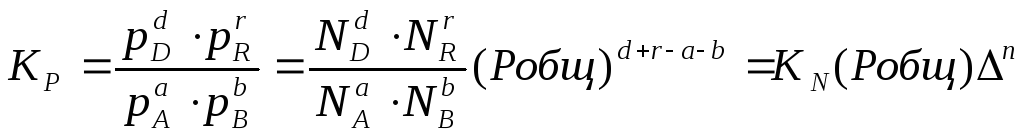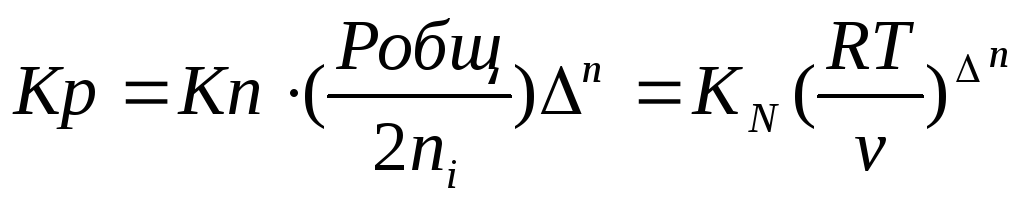Какие способы выражения константы равновесия

Содержание

2.3. Способы выражения константы равновесия
2.4. Смещение химического равновесия
Какие способы выражения константы равновесия

2.3. Способы выражения константы равновесия

Константа равновесия может быть выражена различными способами. Если концентрации веществ, участвующих в реакции, выражены в молярных единицах молярности , т.е. в моль/л, то она обычно обозначается Кс и для равновесия обратимой реакции

записывается в виде:

(2.4)

Для гомогенной газовой реакции константу равновесия удобнее выразить через парциальные давления веществ:

(2.5)

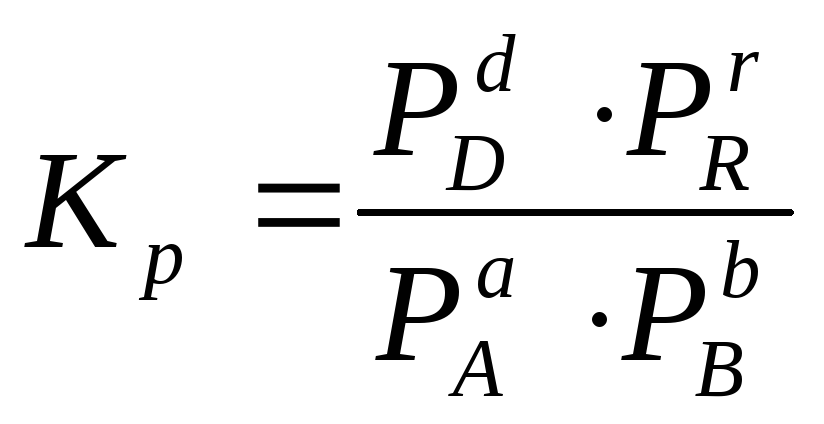
Иногда константу равновесия удобно выразить не через парциальные давления и концентрации, а через количества веществ:

(2.6)

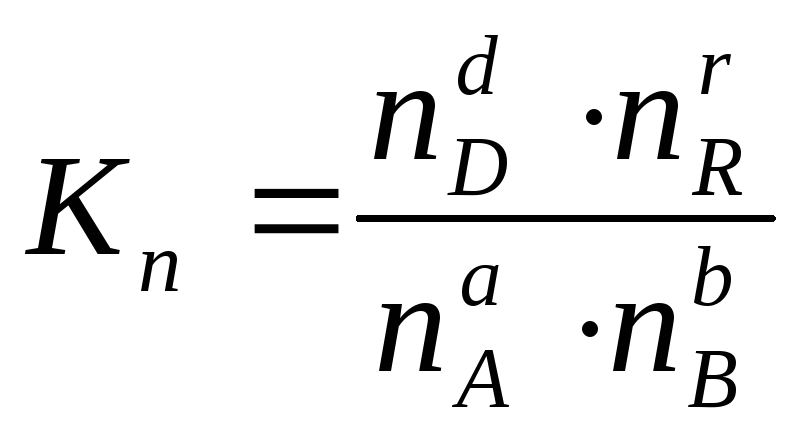
или через соответствующие мольные доли:

(2.7)

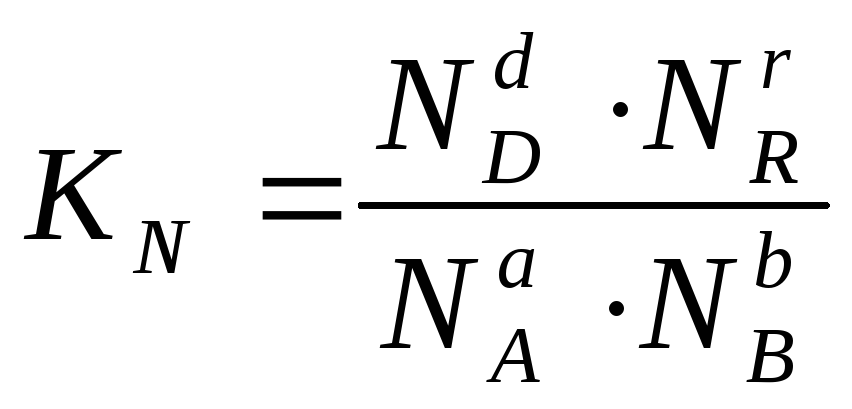
В общем случае константы равновесия Кс, Кр, Кn и К_N различны по значениям. Установим связь между ними.

В газовых системах, для характеристики которых применимо уравнение состояния идеальных газов Менделеева – Клайперона, значение парциального давления любого компонента можно вычислить следующим образом:

(2.8)

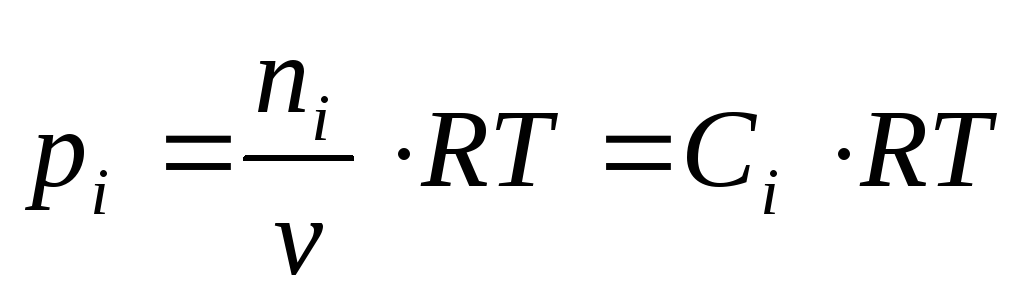
где C – концентрация i-го компонента, выраженная в моль/л. Подставим значение р из уравнения (2.8) в уравнение (2.5) и получим соотношение, которым определяется связь Кс и Кр:

или 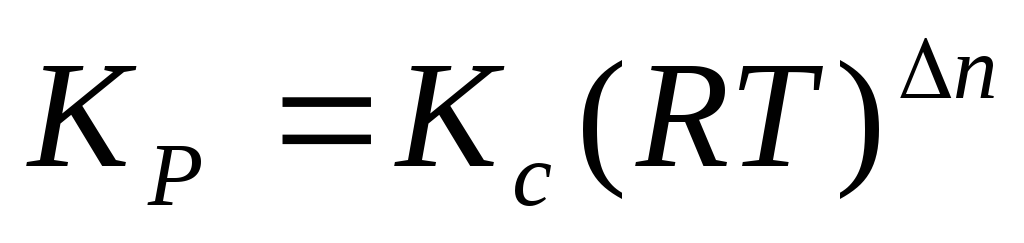, (2.9)

где 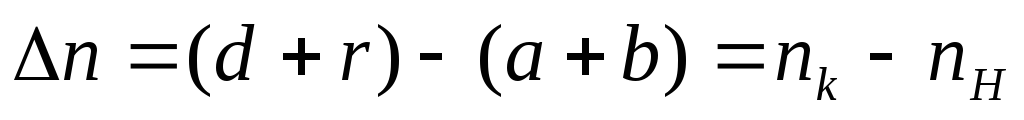– изменение числа моль в результате реакции.

Для идеальных газов парциальные давления связаны с общим давлением Р_общ и мольной долей N_i данного компонента в смеси согласно законам Дальтона следующим равенством:

где р_i – парциальное давление компонента; N_i – мольная доля этого компонента в смеси; Р_общ – общее давление.

Подставим значение р_i в уравнение (2.5), получим:

Воспользовавшись соотношением P_i = N_i∙ Р_общ =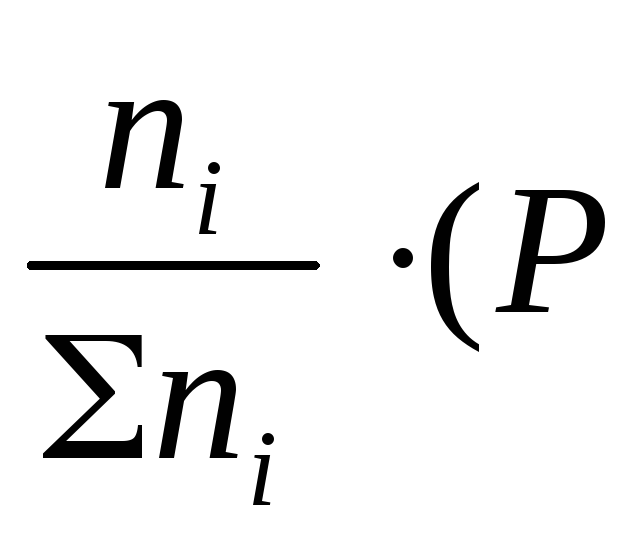_общ) ∆ n ,

где n_i – число моль компонента i в смеси, а n_i – число моль всех компонентов в смеси, получаем:

или

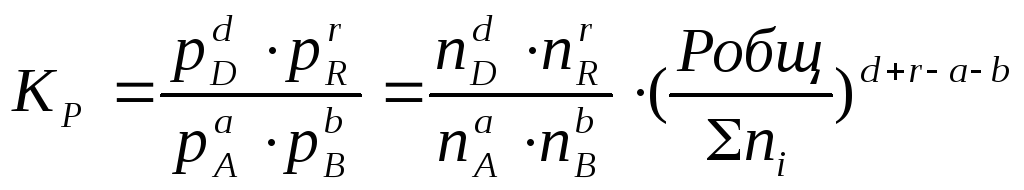
Таким образом, если n≠ 0, т.е. если реакция сопровождается изменением числа моль, то имеет место соотношение:

(2.12).

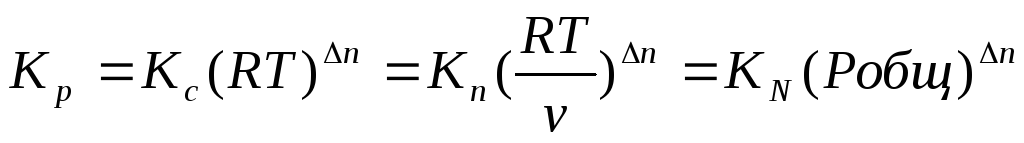
Если же ∆n=0 (реакция не сопровождается изменением числа моль), то К_р = К_с = К_n = K_N , т.е. значения всех видов констант равновесия совпадают.

2.4. Смещение химического равновесия

При постоянных условиях химическое равновесие сохраняется как угодно долго. Однако внешние условия не могут бесконечно оставаться неизменными, а изменение хотя бы одного из них нарушает состояние равновесия, т.е. скорос-

ти прямой и обратной реакций не будут равны между собой (v₁  v₂). Но, так как все физико-химические системы самопроизвольно стремятся к состоянию равновесия, то с течением времени оно вновь установится. Однако, это будет новое равновесие, с другими значениями равновесных концентраций, отвечающими другим, изменившимся условиям.

В каком направлении сместится равновесие при том или ином внешнем воздействии? Ответ на этот вопрос дает принцип Ле-Шателье  Брауна, который можно сформулировать следующим образом: если на систему, находящуюся в состоянии равновесия, оказывается какое – либо внешнее воздействие, то система отвечает таким образом, чтобы это воздействие ослабить. При этом, если в результате нарушения равновесия скорость прямой реакции будет больше скорости обратной реакции, то говорят, что равновесие смещено вправо (v₁  v₂), и соответственно, если преобладает скорость обратной реакции, говорят, что равновесие смещено влево (v₁ v₂ ).

Важнейшими условиями, определяющими состояние химического равновесия, являются:

1) концентрация реагирующих веществ

3) давление (для реакций, протекающих с изменением давления).

Изменение хотя бы одного из них приведет к нарушению равновесия.

Источник

Какие способы выражения константы равновесия

Большинство химических реакций протекают одновременно в двух направлениях: в сторону образования продуктов реакции (прямая реакция) и в сторону разложения последних (обратная реакция). Вследствие химической обратимости реакции не доходят до конца. Скорость прямой реакции уменьшается, а скорость обратной, напротив, возрастает. Когда эти скорости выравниваются наступает состояние химического равновесия.

Так как химически обратимые реакции до перехода в равновесное состояние протекают с конечными скоростями, то с точки зрения термодинамики они не обратимы. Однако можно мысленно представить, что эти реакции идут бесконечно медленно через смежные равновесные состояния. Тогда к ним можно применить общие условия термодинамического равновесия.

Для гомогенных обратимых реакций экспериментально Гульбергом и Ваге был установлен закон действующих масс. При постоянной температуре отношение произведения равновесных концентраций (или парциальных давлений) продуктов реакции к произведению равновесных концентраций (или парциальных равновесий) исходных веществ есть величина постоянная.

Этот экспериментально установленный закон может быть получен методом термодинамических потенциалов. Рассмотрим реакцию в газовой фазе:

аА(г) + b В ↔ сС + dD

Когда система достигает термодинамического равновесия, то термодинамический потенциал при фиксированных естественных переменных достигает минимума. Равновесие, таким образом, можно охарактеризовать выражением химических потенциалов, когда потенциалы продуктов реакции сравняются с потенциалами исходных веществ:

с μ ( с ) + d μ (D) – a μ (a) — b μ (b) = 0 (6 – 1)

Если естественными переменными являются p и T , то = , а = V

Отсюда для систем, подчиняющихся закону идеальных газов, можно получить выражения для μ i

μ i = μ i ° + RTlnCi (6 – 2)

где μ i ° — стандартный химический потенциал.

Подставляется (6 – 2) в (6 – 1) и перенося постоянные величины в левую часть, получаем

сμ C ° + d μ D ° — a μ A ° — b μ B ° = — RTln (6 – 3)

Поскольку в левой части выражение не зависит от концентраций, то выражение под логарифмом является постоянной величиной при постоянной температуре:

Для идеального газа парциальные давления пропорциональны концентрациям, поэтому константа равновесия может быть всегда выражена через равновесные парциальные давления:

Аналогично может быть записано выражение через мольные доли:

Для идеальных газов эти константы связаны между собой соотношением:

где

Следует обратить внимание, что в полученных соотношениях только KN зависит от общего давления. Она позволяет нам оценивать сдвиг равновесия в газовых реакциях при изменении общего давления. Следует иметь в виду, что давление в этих выражениях складывается из парциальных давлений компонентов системы и не учитывает влияние инертных газов, если они присутствуют в реакционной смеси. Естественно инертный газ «разбавляет» компоненты реакционной смеси и поэтому влияет на KN .

Из уравнения (6 – 3) вытекает связь константы равновесия с ∆ rG °:

(6 – 4)

Это уравнение было впервые получено Вант – Гофором методом циклов и получило название уравнения изотермической химической реакции. Очевидно, в этом уравнении ∆ rGT ° относится к этой температуре, при которой определена Кр. Уравнение изотермической химической реакции позволяет определить константу равновесия при заданных условиях не прибегая к исследованию равновесия. Величина ∆ rGT ° может быть рассчитана на основе термических констант для индивидуальных веществ.

Если заданы концентрации (парциальные давления) отличные от равновесных, то можно записать более общий вид уравнения изотермической химической реакции:

Это выражение позволяет определить направление самопроизвольного процесса.

Уравнение изотермы химической реакции позволяет получить выражение для температурной зависимости константы равновесия.

Запишем уравнение Гиббса – Гельмгольца:

Подставим выражение для из (6 – 4)

(6 — 5)

Дифференцируем уравнение (6 – 5)

(6 — 5´)

Из уравнения (6 — 5´) получаем уравнение изобары химической реакции:

(6 – 6)

Если проинтегрировать уравнение (6 – 6) в предположении, что ∆ rHT ° не зависит от температуры, то получим уравнение:

где С – константа интегрирования.

Уравнение (6 – 7) хорошо выполняется в узких интервалах температур и позволяет определить ∆ rGT °.

Для широких интервалов температур ln K р представляют в виде степенных рядов или других аналитических формах:

Такие выражения позволяют рассчитать все термодинамические функции для процессов, для которых данные зависимости получены.

Выражения для термодинамических потенциалов, полученные для идеального газа. Для реальных газов, а особенно для газовых растворов возникают затруднения. Это связано с тем, что расчет концентраций и давлений должен быть проведен исходя из уравнения состояния. Однако для реальных систем единое достаточно простое уравнение состояния получить не удалось.

В связи с этим в термодинамике реальных систем применяется эмпирический метод, предложенный Льюисом. Льюис предложил в уравнениях термодинамики, полученных для идеальных систем заменить давления p на величину летучести f , а концентрации С на активности a .

При такой замене выражения для констант равновесия не меняются по форме. Но этот прием позволяет связать экспериментально найденные свойства реального газа с термодинамическими параметрами.

Летучести и активности – это экспериментальные величины, которые находятся из условия, что для раствора при бесконечном разбавлении или газа при давлении стремящимся к 0 активность приближается к аналитической концентрации, а летучесть к реальному давлению идеального газа. Исходя из этой посылки рассчитываются активности и летучести.

При 1273 К и общем равновесии 30 атм. В равновесной системе

содержится 17% (по общему) . Сколько процентов будет содержаться в газе при общем давлении 20 атм.? При каком давлении в газе будет содержаться 25% ? (Газ считать идеальным).