Какие способы сортировки вы знаете

Алгоритмы и структуры данных для начинающих: сортировка

Авторизуйтесь

Алгоритмы и структуры данных для начинающих: сортировка

В этой части мы посмотрим на пять основных алгоритмов сортировки данных в массиве. Начнем с самого простого — сортировки пузырьком — и закончим «быстрой сортировкой» (quicksort).

Для каждого алгоритма, кроме объяснения его работы, мы также укажем его сложность по памяти и времени в наихудшем, наилучшем и среднем случае.

Метод Swap

Для упрощения кода и улучшения читаемости мы введем метод Swap , который будет менять местами значения в массиве по индексу.

Пузырьковая сортировка

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n)	O(n 2 )	O(n 2 )
Память	O(1)	O(1)	O(1)

Сортировка пузырьком — это самый простой алгоритм сортировки. Он проходит по массиву несколько раз, на каждом этапе перемещая самое большое значение из неотсортированных в конец массива.

27–28 ноября, Москва, Беcплатно

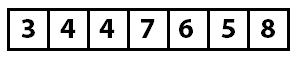
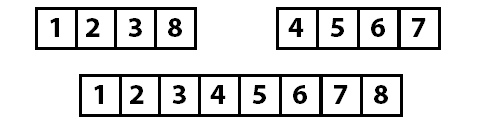
Например, у нас есть массив целых чисел:

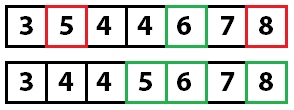
При первом проходе по массиву мы сравниваем значения 3 и 7. Поскольку 7 больше 3, мы оставляем их как есть. После чего сравниваем 7 и 4. 4 меньше 7, поэтому мы меняем их местами, перемещая семерку на одну позицию ближе к концу массива. Теперь он выглядит так:

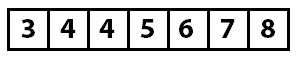
Этот процесс повторяется до тех пор, пока семерка не дойдет почти до конца массива. В конце она сравнивается с элементом 8, которое больше, а значит, обмена не происходит. После того, как мы обошли массив один раз, он выглядит так:

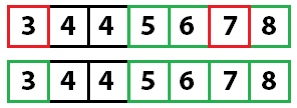
Поскольку был совершен по крайней мере один обмен значений, нам нужно пройти по массиву еще раз. В результате этого прохода мы перемещаем на место число 6.

И снова был произведен как минимум один обмен, а значит, проходим по массиву еще раз.

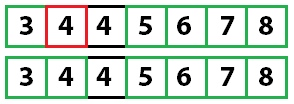
При следующем проходе обмена не производится, что означает, что наш массив отсортирован, и алгоритм закончил свою работу.

Сортировка вставками

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n)	O(n 2 )	O(n 2 )
Память	O(1)	O(1)	O(1)

Сортировка вставками работает, проходя по массиву и перемещая нужное значение в начало массива. После того, как обработана очередная позиция, мы знаем, что все позиции до нее отсортированы, а после нее — нет.

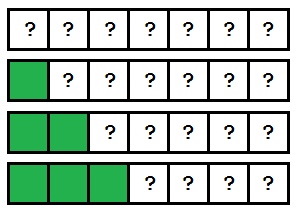
Важный момент: сортировка вставками обрабатывает элементы массива по порядку. Поскольку алгоритм проходит по элементам слева направо, мы знаем, что все, что слева от текущего индекса — уже отсортировано. На этом рисунке показано, как увеличивается отсортированная часть массива с каждым проходом:

Постепенно отсортированная часть массива растет, и, в конце концов, массив окажется упорядоченным.

Давайте взглянем на конкретный пример. Вот наш неотсортированный массив, который мы будем использовать:

Алгоритм начинает работу с индекса 0 и значения 3. Поскольку это первый индекс, массив до него включительно считается отсортированным.

Далее мы переходим к числу 7. Поскольку 7 больше, чем любое значение в отсортированной части, мы переходим к следующему элементу.

На этом этапе элементы с индексами 0..1 отсортированы, а про элементы с индексами 2..n ничего не известно.

Следующим проверяется значение 4. Так как оно меньше семи, мы должны перенести его на правильную позицию в отсортированную часть массива. Остается вопрос: как ее определить? Это осуществляется методом FindInsertionIndex . Он сравнивает переданное ему значение (4) с каждым значением в отсортированной части, пока не найдет место для вставки.

Итак, мы нашли индекс 1 (между значениями 3 и 7). Метод Insert осуществляет вставку, удаляя вставляемое значение из массива и сдвигая все значения, начиная с индекса для вставки, вправо. Теперь массив выглядит так:

Теперь часть массива, начиная от нулевого элемента и заканчивая элементом с индексом 2, отсортирована. Следующий проход начинается с индекса 3 и значения 4. По мере работы алгоритма мы продолжаем делать такие вставки.

Когда больше нет возможностей для вставок, массив считается полностью отсортированным, и работа алгоритма закончена.

Сортировка выбором

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n)	O(n 2 )	O(n 2 )
Память	O(1)	O(1)	O(1)

Сортировка выбором — это некий гибрид между пузырьковой и сортировкой вставками. Как и сортировка пузырьком, этот алгоритм проходит по массиву раз за разом, перемещая одно значение на правильную позицию. Однако, в отличие от пузырьковой сортировки, он выбирает наименьшее неотсортированное значение вместо наибольшего. Как и при сортировке вставками, упорядоченная часть массива расположена в начале, в то время как в пузырьковой сортировке она находится в конце.

Давайте посмотрим на работу сортировки выбором на нашем неотсортированном массиве.

При первом проходе алгоритм с помощью метода FindIndexOfSmallestFromIndex пытается найти наименьшее значение в массиве и переместить его в начало.

Имея такой маленький массив, мы сразу можем сказать, что наименьшее значение — 3, и оно уже находится на правильной позиции. На этом этапе мы знаем, что на первой позиции в массиве (индекс 0) находится самое маленькое значение, следовательно, начало массива уже отсортировано. Поэтому мы начинаем второй проход — на этот раз по индексам от 1 до n — 1.

На втором проходе мы определяем, что наименьшее значение — 4. Мы меняем его местами со вторым элементом, семеркой, после чего 4 встает на свою правильную позицию.

Теперь неотсортированная часть массива начинается с индекса 2. Она растет на один элемент при каждом проходе алгоритма. Если на каком-либо проходе мы не сделали ни одного обмена, это означает, что массив отсортирован.

После еще двух проходов алгоритм завершает свою работу:

Сортировка слиянием

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n·log n)	O(n·log n)	O(n·log n)
Память	O(n)	O(n)	O(n)

Разделяй и властвуй

До сих пор мы рассматривали линейные алгоритмы. Они используют мало дополнительной памяти, но имеют квадратичную сложность. На примере сортировки слиянием мы посмотрим на алгоритм типа «разделяй и властвуй» (divide and conquer).

Алгоритмы этого типа работают, разделяя крупную задачу на более мелкие, решаемые проще. Мы пользуемся ими каждый день. К примеру, поиск в телефонной книге — один из примеров такого алгоритма.

Если вы хотите найти человека по фамилии Петров, вы не станете искать, начиная с буквы А и переворачивая по одной странице. Вы, скорее всего, откроете книгу где-то посередине. Если попадете на букву Т, перелистнете несколько страниц назад, возможно, слишком много — до буквы О. Тогда вы пойдете вперед. Таким образом, перелистывая туда и обратно все меньшее количество страниц, вы, в конце концов, найдете нужную.

Насколько эффективны эти алгоритмы?

Предположим, что в телефонной книге 1000 страниц. Если вы открываете ее на середине, вы отбрасываете 500 страниц, в которых нет искомого человека. Если вы не попали на нужную страницу, вы выбираете правую или левую сторону и снова оставляете половину доступных вариантов. Теперь вам надо просмотреть 250 страниц. Таким образом мы делим нашу задачу пополам снова и снова и можем найти человека в телефонной книге всего за 10 просмотров. Это составляет 1% от всего количества страниц, которые нам пришлось бы просмотреть при линейном поиске.

Сортировка слиянием

При сортировке слиянием мы разделяем массив пополам до тех пор, пока каждый участок не станет длиной в один элемент. Затем эти участки возвращаются на место (сливаются) в правильном порядке.

Давайте посмотрим на такой массив:

Разделим его пополам:

И будем делить каждую часть пополам, пока не останутся части с одним элементом:

Теперь, когда мы разделили массив на максимально короткие участки, мы сливаем их в правильном порядке.

Сначала мы получаем группы по два отсортированных элемента, потом «собираем» их в группы по четыре элемента и в конце собираем все вместе в отсортированный массив.

Для работы алгоритма мы должны реализовать следующие операции:

1. Операцию для рекурсивного разделения массива на группы (метод Sort ).
2. Слияние в правильном порядке (метод Merge ).

Стоит отметить, что в отличие от линейных алгоритмов сортировки, сортировка слиянием будет делить и склеивать массив вне зависимости от того, был он отсортирован изначально или нет. Поэтому, несмотря на то, что в худшем случае он отработает быстрее, чем линейный, в лучшем случае его производительность будет ниже, чем у линейного. Поэтому сортировка слиянием — не самое лучшее решение, когда надо отсортировать частично упорядоченный массив.

Быстрая сортировка

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n·log n)	O(n·log n)	O(n 2 )
Память	O(1)	O(1)	O(1)

Быстрая сортировка — это еще один алгоритм типа «разделяй и властвуй». Он работает, рекурсивно повторяя следующие шаги:

1. Выбрать ключевой индекс и разделить по нему массив на две части. Это можно делать разными способами, но в данной статье мы используем случайное число.
2. Переместить все элементы больше ключевого в правую часть массива, а все элементы меньше ключевого — в левую. Теперь ключевой элемент находится в правильной позиции — он больше любого элемента слева и меньше любого элемента справа.
3. Повторяем первые два шага, пока массив не будет полностью отсортирован.

Давайте посмотрим на работу алгоритма на следующем массиве:

Сначала мы случайным образом выбираем ключевой элемент:

Теперь, когда мы знаем ключевой индекс (4), мы берем значение, находящееся по этому индексу (6), и переносим значения в массиве так, чтобы все числа больше или равные ключевому были в правой части, а все числа меньше ключевого — в левой. Обратите внимание, что в процессе переноса значений индекс ключевого элемента может измениться (мы увидим это вскоре).

Перемещение значений осуществляется методом partition .

На этом этапе мы знаем, что значение 6 находится на правильной позиции. Теперь мы повторяем этот процесс для правой и левой частей массива.

Мы рекурсивно вызываем метод quicksort на каждой из частей. Ключевым элементом в левой части становится пятерка. При перемещении значений она изменит свой индекс. Главное — помнить, что нам важно именно ключевое значение, а не его индекс.

Снова применяем быструю сортировку:

У нас осталось одно неотсортированное значение, а, поскольку мы знаем, что все остальное уже отсортировано, алгоритм завершает работу.

Заключение

На этом мы заканчиваем наш цикл статей по алгоритмам и структурам данных для начинающих. За это время мы рассмотрели связные списки, динамические массивы, двоичное дерево поиска и множества с примерами кода на C#.

Источник

Сортировки и O-нотация

Задача сортировки массива заключается в том, чтобы расставить его элементы в определённом порядке (чаще всего — по неубыванию: каждый элемент должен быть больше или равен предыдущему).

Будет полезно вместе с описанем алгоритмов смотреть их визуализацию.

Сортировка пузырьком

Наш первый подход будет заключаться в следующем: обозначим за \(n\) длину массива и \(n\) раз пройдёмся раз пройдемся по нему, меняя два соседних элемента, если первый больше второго.

Как каждую итерацию максимальный элемент «всплывает» словно пузырек к концу массива — отсюда и название.

После \(i\) шагов алгоритма сортировки пузырьком последние \((i + 1)\) чисел всегда отсортированы, а значит алгоритм работает корректно.

Упражнение. Алгоритм можно немного ускорить. Подумайте, какие лишние элементы мы перебираем. Как нужно изменить границы в двух циклах for , чтобы не делать никаких бесполезных действий?

Сортировка выбором

Другим способом является сортировка выбором минимума (или максимума).

Чтобы отсортировать массив, просто \(n\) раз выберем минимум среди еще неотсортированных чисел и поставим его на свое место. На \(i\) -ом шаге будем искать минимум на отрезке \([i, n — 1]\) и менять его местами с \(i\) -тым элементом, после чего отрезок \([0, i]\) будет отсортирован.

Содержательная часть будет выглядеть так:

Сортировка вставками

Определение. Префиксом длины \(i\) будем называть первые \(i\) элементов массива.

Тогда пусть на \(i\) -ом шаге у нас уже будет отсортирован префикс до \(i\) -го элемента. Чтобы этот префикс увеличить, нужно взять элемент, идущий после него, и менять с левым соседом, пока этот элемент наконец не окажется больше своего левого соседа. Если в конце он больше левого соседа, но меньше правого, то это будет означать, что мы правильно вставили этот элемент в отсортированную часть массива.

Сортировка подсчетом

Предыдущие три алгоритма работали с массивами, в которых лежат абсолютно любые объекты, которые можно сравнивать: любые числа, строки, пары, другие массивы — почти все что угодно.

Но особых случаях, когда элементы принадлежат какому-то маленькому множеству, можно использовать другой алгоритм — сортировку подсчетом.

Пусть, например, нам гарантируется, что все числа натуральные и лежат в промежутке от \(1\) до \(100\) . Тогда есть такой простой алгоритм:

Создадим массив размера \(100\) , в котором будем хранить на \(k\) -ом месте, сколько раз число \(k\) встретилось в этом массиве.

Пройдемся по всем числам исходного массива и увеличим соответствующее значение массива на \(1\) .

После того, как мы посчитали, сколько раз каждое число встретилось, можно просто пройтись по этому массиву и вывести \(1\) столько раз, сколько встретилась \(1\) , вывести \(2\) столько раз, сколько встретилась \(2\) , и так далее.

Время работы такого алгоритма составляет \(O(M+N)\) , где \(M\) — число возможных значений, \(N\) — число элементов в массиве. Сейчас мы расскажем, что же это означает.

О-нотация

Часто требуется оценить, сколько времени работает алгоритм. Но тут возникают проблемы:

• на разных компьютерах время работы всегда будет слегка отличаться;
• чтобы измерить время, придётся запустить сам алгоритм, но иногда приходится оценивать алгоритмы, требующие часы или даже дни работы.

Зачастую основной задачей программиста становится оптимизировать алгоритм, выполнение которого займёт тысячи лет, до какого-нибудь адекватного времени работы. Поэтому хотелось бы уметь предсказывать, сколько времени займёт выполнение алгоритма ещё до того, как мы его запустим.

Для этого сначала попробуем оценить число операций в алгоритме. Возникает вопрос: какие именно операции считать. Как один из вариантов — учитывать любые элементарные операции:

• арифметические операции с числами: +, -, *, /
• сравнение чисел: , =, ==, !=
• присваивание: a[0] = 3

При этом надо учитывать, как реализованы некоторые отдельные вещи в самом языке. Например, в питоне срезы массива ( array[3:10] ) копируют этот массив, то есть этот срез работает за 7 элементарных действий. А swap , например, может работать за 3 присваивания.

Упражнение. Попробуйте посчитать точное число сравнений и присваиваний в сортировках пузырьком, выбором, вставками и подсчетом в худшем случае (это должна быть какая формула, зависящая от \(n\) — длины массива).

Чтобы учесть вообще все элементарные операции, ещё надо посчитать, например, сколько раз прибавилась единичка внутри цикла for . А ещё, например, строчка n = len(array) — это тоже действие. Поэтому даже посчитав их, сразу очевидно, какой из этих алгоритмов работает быстрее — сравнивать формулы сложно. Хочется придумать способ упростить эти формулы так, чтобы:

• не нужно было учитывать много информации, не очень сильно влияющей на итоговое время;
• легко было оценивать время работы разных алгоритмов для больших чисел;
• легко было сравнивать алгоритмы на предмет того, какой из них лучше подходит для тех или иных входных данных.

Для этого придумали \(O\) -нотацию — асимптотическое время работы вместо точного (часто его ещё называют асимптотикой).

Определение. Пусть \(f(n)\) — это какая-то функция. Говорят, что алгоритм работает за \(O(f(n))\) , если существует число \(C\) , такое что алгоритм работает не более чем за \(C \cdot f(n)\) операций.

В таких обозначениях можно сказать, что

• сортировка пузырьком работает за \(O(n^2)\) ;
• сортировка выбором работает за \(O(n^2)\) ;
• сортировка вставками работает за \(O(n^2)\) ;
• сортировка подсчетом работает за \(O(n + m)\) .

Это обозначение удобно тем, что оно короткое и понятное, а также оно не зависит от умножения на константу или прибавления константы. Например, если алгоритм работает за \(O(n^2)\) , то это может значить, что он работает за \(n^2\) , за \(n^2 + 3\) , за \(\frac<2>\) или даже за \(1000 \cdot n^2 + 1\) действие. Главное — что функция ведет себя как \(n^2\) , то есть при увеличении \(n\) (в данном случае это длина массива) он увеличивается как некоторая квадратичная функция. Например, если увеличить \(n\) в 10 раз, время работы программы увеличится приблизительно в 100 раз.

Все рассуждения про то, сколько операций в swap или считать ли отдельно присваивания, сравнения и циклы — отпадают. Каков бы ни был ответ на эти вопросы, они меняют ответ лишь на константу, а значит асимптотическое время работы алгоритма никак не меняется.

Первые три сортировки именно поэтому называют квадратичными — они работают за \(O(n^2)\) . Сортировка подсчетом может работать намного быстрее — она работает за \(O(n + m)\) , а если в задаче \(M \leq N\) , то это вообще линейная функция \(O(n)\) .

Упражнение. Найдите асимптотику данных функций, маскимально упростив ответ (например, до \(O(n)\) , \(O(n^2)\) и т. д.):

Упражнение. Найдите асимптотическое время работы данных функций:

Упражнение. Найдите лучшее время работы алгоритмов, решающих данные задачи:

• Написать числа от \(1\) до \(n\) .
• Написать все тройки чисел от \(1\) до \(n\) .
• Найти разницу между максимумом и минимумом в массиве.
• Найти число единиц в бинарной записи числа \(n\) .

Сортировки за \(O(n \log n)\)

Сортировка очень часто применяется как часть решения олимпиадных задач. В таких случаях обычно не пишут её заново, а используют встроенную.

Пример на Python:

В разных языках она может быть реализована по-разному, но везде она работает за \(O(n \log n)\) , и, обычно, неплохо оптимизирована. Далее мы опишем два подхода к её реализации.

Сортировка слиянием

Найти количество пар элементов \(a\) и \(b\) в отсортированном массиве, такие что \(b — a > K\) .

Наивное решение: бинарный поиск. Будем считать, что массив уже отсортирован. Для каждого элемента \(a\) найдем первый справа элемент \(b\) , который входит в ответ в паре с \(a\) . Нетрудно заметить, что все элементы, большие \(b\) , также входят в ответ. Итоговая асимптотика \(O(n\log n)\) .

А можно ли быстрее?

Да, давайте перебирать два указателя — два индекса \(first\) и \(second\) . Будем перебирать \(first\) просто слева направо и поддерживать для каждого \(first\) первый элемент справа от него, такой что \(a[second] — a[first] > K\) как \(second\) . Тогда в пару к \(a=a[first]\) подходят ровно \(n-second\) элементов массив начиная с \(second\) .

За сколько же работает это решение? С виду может показаться, что за \(O(n^2)\) , но давайте посмотрим сколько раз меняется значение переменной \(second\) . Так как оно изначально равняется нулю, только увеличивается и не может превысить \(n\) , то суммарно операций мы сделаем \(O(n)\) .

Это называется метод двух указателей — так как мы двигаем два указателя first и second одновременно слева направо по каким-то правилам. Обычно его используют на одном отсортированном массиве.

Давайте разберем еще примеры.

Слияние

Еще пример двух указателей на нескольких массивах.

Пусть у нас есть два отсортированных по неубыванию массива размера \(n\) и \(m\) . Хотим получить отсортированный массив размера \(n + m\) из исходных.

Пусть первый указатель будет указывать на начало первого массива, а второй, соответственно, на начало второго. Из двух текущих элементов, на которые указывают указатели, выберем наименьший и положим на соответствующую позицию в новом массиве, после чего сдвинем указатель. Продолжим этот процесс пока в обоих массивах не закончатся элементы. Тогда код будет выглядеть следующим образом:

Итоговая асимптотика: \(O(n + m)\) .

Сортировка слиянием

Давайте подробно опишем как использовать операцию слияния для сортировки за \(O(n\log n)\) .

Пусть у нас есть какой-то массив.

Сделаем такое предположение. Пусть мы уже умеем как-то сортировать массив размера \(n\) . Тогда научимся сортировать массив размера \(2n\) . Давайте разобьем наш массив на две половины, отсортируем каждую из них, а после это сделаем слияние двух массивов, которое мы научились делать за \(O(n)\) в данных условиях. Также заметим, что массив размера \(1\) уже отсортирован, тогда мы можем делать это процедуру рекурсивно. Тогда для данного массива \(a\) это будет выглядеть следующим образом:

Так сколько же работает это решение?

Пускай \(T(n)\) — время сортировки массива длины \(n\) , тогда для сортировки слиянием справедливо \(T(n)=2T(n/2)+O(n)\) \(O(n)\) — время, необходимое на то, чтобы слить два массива длины n. Распишем это соотношение:

Количество инверсий

Пусть у нас есть некоторая перестановка \(a\) . Инверсией называется пара индексов \(i\) и \(j\) такая, что \(i и \(a[i] > a[j]\) .

Найти количество инверсий в данной перестановке.

Очевидно, что эта задача легко решается обычным перебором двух индексов за \(O(n^2)\) :

Внезапно эту задачу можно решить используя сортировку слиянием, слегка модифицируя её. Оставим ту же идею. Пусть мы умеем находить количество инверсий в массиве размера \(n\) , научимся находить количество инверсий в массиве размера \(2n\) .

Заметим, что мы уже знаем количество инверсий в левой половине и в правой половине массива. Осталось лишь посчитать число инверсий, где одно число лежит в левой половине, а второе в правой половине. Как же их посчитать?

Давайте подробнее рассмотрим операцию merge левой и правой половины (которую мы ранее заменили на вызов встроенной функции merge). Первый указатель указывает на элемент левой половины, второй указатель указывает на элемент второй половины, мы смотрим на минимум из них и этот указатель вдигаем вправо.

Рассмотрим число \(A\) в левой половине. В скольки инверсиях между половинами оно участвует? В стольки, сколько чисел в правой половине меньше, чем оно. Знаем ли мы это количество? Да! Ровно в тот момент, когда мы число \(A\) вносим в слитый массив, второй указатель указывает на первое число в правой половине, которое больше чем \(A\) .

Значит в тот момент, когда мы добавляем число \(A\) из левой половины, к ответу достаточно прибавить индекс второго указателя (минус начало правой половины). Так мы учтем все инверсии между половинами.

Быстрая сортировка

Быстрая сортировка заключается в том, что на каждом шаге мы находим опорный элемент, все элементы, которые меньше его кидаем в левую часть, остальные в правую, а затем рекурсивно спускаемся в обе части.

Давайте оценим асимптотику данной сортировки. На случайных данных она работает за \(O(NlogN)\) , так как каждый раз мы будем делить массив на две примерно равные части, то есть суммарно размер рекурсии будет около логарифма и при этом на каждом этапе рекурсии мы просмотрим не более, чем размер массива. Однако можно легко найти две проблемы, одна — одинаковые числа, а вторая — если вдруг середина — минимум или максимум.

Существуют несколько выходов из этой ситуации :

Давайте если быстрая сортировка работает долго, то запустим любую другую сортировку за \(NlogN\) .

Давайте делить массив не на две, а на три части(меньше, равны, больше).

Чтобы избавиться от проблемы с максимумом/минимумом в середине, давайте брать случайный элемент.

Поиск \(k\) -ой порядковой статистики за \(O(N)\)

Пусть дан массив \(A\) длиной \(N\) и пусть дано число \(K\) . Задача заключается в том, чтобы найти в этом массиве \(K\) -ое по величине число, т.е. \(K\) -ую порядковую статистику.

Давайте поймем, что в быстрой сортировке мы можем узнать, сколько элементов меньше данного, тогда рассмотрим три случая

количество чисел, меньше данного = \(k — 1\) , тогда наше число — ответ.

количество чисел, меньше данного >= \(k\) , тогда спускаемся рекурсивно в левую часть и ищем там ответ.

количество чисел, меньше данного \(k\) , спускаемся в правую ищем ( \(k\) — левая — 1) — ое число.

За сколько же это работает, из быстрой сортировки мы имеем, что размер убывает приблизительно в 2 раза, то есть мы имеем сумму \(\sum_^n <2 ^ k>= <2^-1>\) что в нашем случае это максимум равно \(2 * N — 1\) , то есть \(O(N)\) .

Также в C++ эта функция уже реализована и называется nth_element .

Источник