Какие способы применяют для определения скоростей точек тела при плоскопараллельном движении

Техническая механика

Плоскопараллельное движение

Понятие о плоскопараллельном движении

Плоскопараллельным движением твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях, параллельных какой-то одной плоскости, называемой основной плоскостью.

Примерами плоскопараллельного движения могут служить движение колеса на прямолинейном участке пути, движение шатуна кривошипно-ползунного механизма.

Из определения плоскопараллельного движения следует, что любая прямая АВ , проведенная в теле перпендикулярно основной плоскости, движется поступательно. Для определения движения тела на каждой прямой, перпендикулярной основной плоскости, достаточно знать движение только одной точки.
Взяв эти точки в одной плоскости, параллельной основной, получим сечение S , движение которого будет определять движение всего тела.

Но плоское движение сечения S вполне может быть определено движением любых двух точек, лежащих в этом сечении. На основании этого можно утверждать, что плоскопараллельное движение тела может быть определено движением отрезка прямой в плоскости, параллельной основной.

Плоскопараллельное движение изучается двумя методами: методом мгновенных центров скоростей и методом разложения плоскопараллельного движения на простейшие движения — поступательное и вращательное.

Метод мгновенных центров скоростей

В основе этого метода лежит следующая теорема: всякое плоскопараллельное перемещение твердого тела может быть получено одним вращением около оси, перпендикулярной основной плоскости .

Пусть отрезок, определяющий плоскопараллельное движение тела, за конечный промежуток времени переместился из положения АВ в положение А₁В₁ (см. рис. 3) .

Соединим точки А и А₁ , В и В₁ прямыми линиями и из середин полученных отрезков (точек М и N ) восстановим перпендикуляры до их взаимного пересечения в точке О . Эту точку соединим с концами отрезков АВ и А₁ВВ₁ прямыми линиями, и получим при этом два равных (конгруэнтных) треугольника, имеющих общую вершину О :

Треугольник АОВ совмещается с треугольником А₁ОВ₁ путем поворота на угол φ вокруг точки О , называемой центром конечного поворота .
Точка О есть след оси конечного поворота, перпендикулярной основной плоскости. Таким образом, отрезок АВ , определяющий плоскопараллельное движение тела, перемещается в любое новое положение путем одного вращения вокруг оси конечного поворота.

Приведенное доказательство будет справедливо и в том случае, если перемещение тела произойдет за бесконечно малый промежуток времени Δt .
В пределе при Δt стремящемся к нулю, вращение будет происходить вокруг мгновенной оси, след которой в плоскости фигуры называется мгновенным центром скоростей .

Очевидно, что скорость точки, являющейся в данный момент мгновенным центром скоростей, равна нулю. Угловая скорость ω , с которой происходит мгновенное вращение, называется мгновенной угловой скоростью.

Точка неподвижной плоскости, совпадающая в данный момент времени с мгновенным центром скоростей плоской фигуры, называется мгновенным центром вращения .

Если прямая АВ движется параллельно самой себе, то можно полагать, что тело вращается вокруг оси, удаленной в бесконечность, иначе говоря, поступательное движение можно рассматривать, как вращательное по кругу бесконечно большого радиуса.

Таким образом, плоскопараллельное движение тела может рассматриваться, как непрерывная цепь последовательных мгновенных поворотов вокруг мгновенных осей вращения.

Следует отметить, что методом мгновенных центров скоростей можно пользоваться только для определения скоростей точке плоской фигуры, но не при определении траекторий и ускорений этих точек.

Свойства мгновенного центра скоростей

Рассматривая в каждый момент времени сложное плоскопараллельное движение как простейшее — вращательное, можно для вычисления скоростей точек твердого тела применять формулы вращательного движения.

Из закона распределения скоростей точек твердого тела, вращающегося вокруг неподвижной оси, можно установить следующие свойства мгновенного центра скоростей:

• Скорость мгновенного центра скоростей равна нулю;
• Мгновенный центр скоростей лежит на перпендикуляре, восстановленном из точки к направлению ее скорости;
• Скорость точки равна произведению мгновенной угловой скорости на расстояние точки от мгновенного центра скоростей (см. рис. 4) : v_А = ωОА .

На основании этих свойств можно установить следующие способы определения положения мгновенного центра скоростей плоской фигуры, определяющей плоскопараллельное движение:

1. Если известны мгновенная угловая скорость ω и скорость vА точки А плоской фигуры, то мгновенный центр скоростей будет находиться на перпендикуляре, восстановленном из точки А к вектору скорости v_А на расстоянии ОА = v_А/ω (см. рис 4) .

2 . Если известны направления скоростей двух точек А и В плоской фигуры (рис. 5а) , то мгновенный центр скоростей будет находиться на точке О пересечения двух перпендикуляров, восстановленных из точек А и В к направлениям их скоростей, причем

т. е. скорости точек плоской фигуры прямо пропорциональны их расстояниям от мгновенного центра скоростей.

3. Если известно, что скорости двух точек А и В плоской фигуры параллельны друг другу, направлены в одну сторону, перпендикулярны отрезку АВ и по модулю не равны (рис. 5б) , то мгновенный центр скоростей О будет находиться в точке пересечения прямой, соединяющей начала векторов v_А и v_В с прямой, соединяющей концы этих векторов.
Если векторы скоростей А и В равны между собой, то мгновенный центр скоростей в данный момент времени находится в бесконечности, мгновенная угловая скорость ω равна нулю, скорости всех точек плоской фигуры будут одинаковы и движение будет мгновенно поступательным.

4. Если скорости двух точек А и В плоской фигуры параллельны друг другу, направлены в противоположные стороны и перпендикулярны отрезку АВ (см. рис. 5в) , то мгновенный центр скоростей О будет находиться в точке пересечения отрезка АВ с прямой, соединяющей концы векторов v_А и v_В .

5. Если плоская фигура катится без скольжения по неподвижной кривой, мгновенный центр скоростей О будет находиться в точке соприкосновения фигуры с кривой, так как скорость этой точки фигуры относительно кривой равна нулю (скольжение отсутствует).

На рис. 6 приведены положения мгновенного центра скоростей (МЦС) и графики скоростей точек вертикального диаметра колеса при различных случаях его качения по прямолинейному рельсу (скольжение, качение, буксование и т. п.).

Разложение плоскопараллельного движения на вращательное и поступательное

В основе этого метода лежит следующая теорема: всякое плоскопараллельное перемещение твердого тела может быть получено с помощью одного вращательного и одного поступательного движения.

Пусть за время Δt отрезок АВ , определяющий плоскопараллельное движение тела, переместился в положение А₁В₁ . Предположим, что отрезок АВ вначале перемещался только поступательно, причем все его точки двигались одинаково, как, например, точка А . Таким образом, отрезок переместился в положение А₁В₂ , после чего его можно переместить в положение А₁В₁ посредством только вращательного движения вокруг точки А₁ .
Очевидно, что сложное плоскопараллельное движение состоит из двух простейших движений – поступательного и вращательного, причем можно считать, что эти движения совершаются одновременно.

Установим зависимость между векторами скоростей точек А и В . Для этого соединим прямыми точки А , А₁ и В , В₁ , в результате чего получим следующую зависимость между векторами перемещений точки В :

Так как ВВ₂ = АА₁ , то можно записать, что ВВ₁ = АА₁ + В₂В₁ .
Разделим все члены равенства на Δt и перейдем к пределу при Δt стремящемся к нулю:

где v_А и v_В – векторы абсолютных скоростей соответствующих точек, v_ВА – вектор скорости точки В в относительном вращательном движении отрезка АВ вокруг точки А , направленный перпендикулярно отрезку АВ .

Таким образом, плоскопараллельное движение тела может осуществляться путем одновременно происходящих вращательного и поступательного движений; поступательное движение можно считать переносным, а вращательное – относительным.
Вектор абсолютной скорости произвольной точки В равен вектору абсолютной скорости любой другой точки А плюс вектор скорости точки В в относительном вращательном движении отрезка АВ вокруг точки А .

Точку, вокруг которой происходит относительное вращательное движение, называют полюсом .

Если за полюс вместо точки А принять точку В , то, рассуждая аналогично, получим:

Если сравнить это векторное равенство с предыдущим, становится очевидным, что векторы относительных скоростей v_ВА и v_АВ по модулю равны между собой, т. е. v_ВА = v_АВ .

Из рис. 7 видно, что направление относительного вращения и угол поворота отрезка АВ за какой-то промежуток времени не зависит от выбора полюса, т. е. φ_ВА = φ_АВ .

Продифференцировав это равенство по времени, получим:

Следовательно, относительная угловая скорость от выбора полюса не зависит. Аналогичный вывод можно сделать и об относительном угловом ускорении:

dωBA/dt = dωAB/dt или αВА= αАВ .

На основании вышеизложенного можно сделать вывод, что при разложении плоскопараллельного движения на поступательное и вращательное поступательная составляющая движения в общем случае зависит от выбора полюса, а вращательная составляющая от выбора полюса не зависит.

Так как за полюс может быть выбрана любая точка плоскости, в том числе и мгновенный центр скоростей, то при разложении плоскопараллельного движения на поступательное и вращательное угловая скорость относительного вращательного движения всегда равна абсолютной угловой скорости.

Если векторное равенство v_А = v_В + v_АВ спроецировать на направление прямой АВ , то получим, что проекция v_А равна проекции v_В , так как проекция v_АВ равна нулю. Следовательно, при плоскопараллельном движении проекции скоростей двух точек плоской фигуры на направление прямой, соединяющей эти точки, равны между собой.

Источник

3. Кинематика плоскопараллельного движения тела

3.1. Определение скоростей точек тела при плоскопараллельном движении

Изучение плоскопараллельного движения тела можно свести к изучению движения плоской фигуры, образованной сечением тела плоскостью, параллельной неподвижной плоскости, относительно которой движется тело.

Определение скоростей точек плоской фигуры можно выполнить одним их следующих методов:

основанным на использовании векторного уравнения;

основанным на использовании теоремы о проекциях скоростей точек тела на прямую, проходящую через эти точки;

основанным на использовании мгновенного центра скоростей.

Наиболее часто применяется последний метод, ему ниже будет уделено основное внимание.

3.1.1. Аналитический метод

При использовании аналитического метода считаются известными уравнения движения плоской фигуры (тела, совершающего плоскопараллельное движение):(3.1)

Тогда координаты точки М (рис. 3.1) будут

(3.2)

где b – расстояние от точки М до полюса А.

Модуль скорости точки М определяется по формуле (1.2)

.

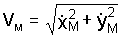
Направление вектора  V_м определяется по направляющим косинусам:

Таким образом, задача по определению скоростей точек плоской фигуры сводится к известному решению соответствующей задачи кинематики точки.

Угловая скорость плоской фигуры определяется дифференцированием последнего уравнения из (3.1), т.е.

. (3.3)

Аналитический метод решения задачи рекомендуется использовать в тех случаях, когда требуется определить скорости точек для большого числа положений плоской фигуры.

3.1.2. Метод, основанный на использовании векторного уравнения

Векторное уравнение для скоростей точек плоской фигуры получается из теоремы: скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и скорости этой точки при вращении фигуры вокруг полюса, т.е. (рис. 3.2)

, (3.4)

где  V_А – скорость полюса А;  V_М/А – скорость точки М при вращении плоской фигуры вокруг полюса А.

Скорость  V_М/А направлена перпендикулярно прямой АМ в сторону вращения фигуры (рис. 3.2) и равна по модулю

, (3.5)

где  – угловая скорость вращения плоской фигуры.

Чтобы можно было определить скорость точки М, используя уравнение (3.4), необходимо знать скорость полюса А и угловую скорость вращения плоской фигуры . Для решения задачи надо построить по уравнению (3.4) параллелограмм скоростей (рис. 3.2).

Диагональ этого параллелограмма есть искомая скорость точки  V_М, ее модуль:

. (3.6)

Решение задачи рекомендуется начинать с изображения плоской фигуры в положении, соответствующем данному моменту времени. Затем следует выбрать полюс и для заданной точки М записать векторное уравнение (3.4). За полюс следует взять точку тела, скорость которой задана. Далее необходимо построить параллелограмм скоростей по уравнению (3.4), вычислить модуль скорости V_М/А по формуле (3.5), а затем модуль скорости точки V_М по формуле (3.6).

Источник