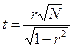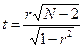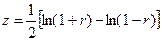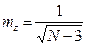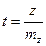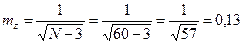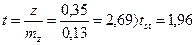Оценка достоверности коэффициента корреляции Пирсона



Существует 3 способа оценки достоверности коэффициента корреляции:
1. Оценка достоверности на основе критерия Стьюдента. В выборках, объём которых больше 100, критерий «t» вычисляется по формуле:
При меньших объемах выборок коэффициент «t» вычисляется по формуле:
Если t≥ tst нулевая гипотеза отклоняется, то есть корреляция достоверна. Если t ≤ tst нулевая гипотеза принимается, то есть корреляция недостоверна.
2. Оценка достоверности на основе использования критических значений коэффициента корреляции (приложение 2.7). Соответствующая таблица имеет два входа: число степеней свободы (строчки) и уровень значимости (столбцы). На их пересечении определяется критическое значение коэффициента корреляции (rst).
Число степеней свободы (df) вычисляется по формуле df= N— 2. При изучении корреляции обычно используют 5% уровень значимости. Если эмпирическое значение r >rst, нулевая гипотеза отклоняется, следовательно, корреляция достоверна. Если эмпирическое значение r
Величину «z» предложил использовать Р.Фишер. Формула вычисления величины «z» следующая:
Для оценки достоверности коэффициента корреляции на основе z—преобразования необходимо:
1) преобразовать «r» в «z» по специальной таблице (приложение 2.8);
2) вычислить ошибку «z» по формуле:
3) вычислить критерий «t»:
4) определить стандартное значение критерия «tst» по таблице при df = N— 2;
5) сформулировать статистический вывод: если t≥ tst нулевая гипотеза отклоняется, то есть корреляция достоверна; если t ≤ tst нулевая гипотеза принимается, то есть, корреляция недостоверна.
Пример 5. Оценить достоверность r=0,34 (N=60).
Первый способ: Поскольку N 0,25, следовательно, нулевая гипотеза отклоняется, корреляция достоверна.
Третий способ: Преобразуем «r» в «z» по специальной таблице: r→z = 0,34→0,35. Вычисляем ошибку «z»:
Вычисляем критерий Стьюдента и сравниваем его со стандартным значением:
Статистический вывод: нулевая гипотеза отклоняется, то есть, корреляция достоверна.
Источник
Какие способы оценки достоверности полученного значения коэффициента могут быть использованы
При изучении общественного здоровья и здравоохранения в научных и практических целях исследователю часто приходится проводить статистический анализ связей между факторными и результативными признаками статистический совокупности (причинно-следственная связь) или определение зависимости параллельных изменений нескольких признаков этой совокупности от какой либо третьей величины (от общей их причины). Необходимо уметь изучать особенности этой связи, определять ее размеры и направление, а также оценивать ее достоверность. Для этого используются методы корреляции.
- Виды проявления количественных связей между признаками
- функциональная связь
- корреляционная связь
Определения функциональной и корреляционной связи
Функциональная связь — такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-математических процессов.
Корреляционная связь — такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для медико-биологических процессов.
Практическое значение установления корреляционной связи. Выявление причинно-следственной между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.)
Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др.
Величина, характеризующая направление и силу связи между признаками. Коэффициент корреляции, который одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до ± 1
- график (диаграмма рассеяния)
- коэффициент корреляции
- прямая
- oбратная
- сильная: ±0,7 до ±1
- средняя: ±0,3 до ±0,699
- слабая: 0 до ±0,299
- метод квадратов (метод Пирсона)
- ранговый метод (метод Спирмена)
- измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту)
- расчет может производиться с использованием абсолютных или производных величин
- для вычисления коэффициента корреляции используются не сгруппированные вариационные ряды (это требование применяется только при вычислении коэффициента корреляции по методу квадратов)
- число наблюдений не менее 30
- когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных
- когда признаки представлены не только количественными, но и атрибутивными значениями
- когда ряды распределения признаков имеют открытые варианты (например, стаж работы до 1 года и др.)
- когда требуется точное установление силы связи между признаками
- когда признаки имеют только количественное выражение
Методика и порядок вычисления коэффициента корреляции
1) Метод квадратов
- построить вариационные ряды для каждого из сопоставляемых признаков, обозначив первый и второй ряд чисел соответственно х и у;
- определить для каждого вариационного ряда средние значения (М1 и М2);
- найти отклонения (dх и dy) каждого числового значения от среднего значения своего вариационного ряда;
- полученные отклонения перемножить (dx X dy)
- каждое отклонение возвести в квадрат и суммировать по каждому ряду (Σ dx 2 и dy 2 )
- подставить полученные значения в формулу расчета коэффициента корреляции:
при наличии вычислительной техники расчет производится по формуле: 
2) Ранговый метод
- составить два ряда из парных сопоставляемых признаков, обозначив первый и второй ряд соответственно х и у. При этом представить первый ряд признака в убывающем или возрастающем порядке, а числовые значения второго ряда расположить напротив тех значений первого ряда, которым они соответствуют
- величину признака в каждом из сравниваемых рядов заменить порядковым номером (рангом). Рангами, или номерами, обозначают места показателей (значения) первого и второго рядов. При этом числовым значениям второго признака ранги должны присваиваться в том же порядке, какой был принят при раздаче их величинам первого признака. При одинаковых величинах признака в ряду ранги следует определять как среднее число из суммы порядковых номеров этих величин
- определить разность рангов между х и у (d): d = х — у
- возвести полученную разность рангов в квадрат (d 2 )
- получить сумму квадратов разности (Σ d 2 ) и подставить полученные значения в формулу:
Схема оценки корреляционной связи по коэффициенту корреляции
| Сила связи | Направление связи | |
| прямая (+) | обратная (-) | |
| Сильная | от + 1 до +0,7 | от — 1 до — 0,7 |
| Средняя | от + 0,699 до + 0,3 | от — 0,699 до — 0,3 |
| Слабая | от + 0,299 до 0 | от — 0,299 до 0 |
Вычисление ошибки коэффициента корреляции
- ошибка коэффициента корреляции, вычисленного методом квадратов (Пирсона):
ошибка коэффициента корреляции, вычисленного ранговым методом (Спирмена):

Оценка достоверности коэффициента корреляции,полученного методом ранговой корреляции и методом квадратов
Способ 1
Достоверность определяется по формуле:
Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n — 2), где n — число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности р ≥99%.
Способ 2
Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n — 2), он равен или более табличного, соответствующего степени безошибочного прогноза р ≥95%.
на применение метода квадратов
Задание: вычислить коэффициент корреляции, определить направление и силу связи между количеством кальция в воде и жесткостью воды, если известны следующие данные (табл. 1). Оценить достоверность связи. Сделать вывод.
| Жесткость воды (в градусах) | Количество кальция в воде (в мг/л) |
| 4 8 11 27 34 37 | 28 56 77 191 241 262 |
Обоснование выбора метода. Для решения задачи выбран метод квадратов (Пирсона), т.к. каждый из признаков (жесткость воды и количество кальция) имеет числовое выражение; нет открытых вариант.
Решение.
Последовательность расчетов изложена в тексте, результаты представлены в таблице. Построив ряды из парных сопоставляемых признаков, обозначить их через х (жесткость воды в градусах) и через у (количество кальция в воде в мг/л).
| Жесткость воды (в градусах) | Количество кальция в воде (в мг/л) | dх | dу | dх х dу | dx 2 | dy 2 |
| 4 8 11 27 34 37 | 28 56 77 191 241 262 | -16 -12 -9 +7 +14 +16 | -114 -86 -66 +48 +98 +120 | 1824 1032 594 336 1372 1920 | 256 144 81 49 196 256 | 12996 7396 4356 2304 9604 14400 |
| Мх=Σ х / n | Му=Σ у / n | Σ dх x dу=7078 | Σ dх 2 =982 | Σ dy 2 =51056 | ||
| Мх=120/6=20 | Мy=852/6=142 |
- Определить средние величины Mx ряду вариант «х» и Му в ряду вариант «у» по формулам:
Мх = Σх/n (графа 1) и
Му = Σу/n (графа 2) - Найти отклонение (dх и dу) каждой варианты от величины вычисленной средней в ряду «x» и в ряду «у»
dх = х — Мх (графа 3) и dy = у — Му (графа4). - Найти произведение отклонений dx х dy и суммировать их: Σ dх х dу (графа 5)
- Каждое отклонение dx и dу возвести в квадрат и суммировать их значения по ряду «х» и по ряду «у»: Σ dx 2 = 982 (графа 6) и Σ dy 2 = 51056 (графа 7).
- Определить произведение Σ dx 2 х Σ dy 2 и из этого произведения извлечь квадратный корень
Полученные величины Σ (dx x dy) и √ (Σdx 2 x Σdy 2 ) подставляем в формулу расчета коэффициента корреляции:
Определить достоверность коэффициента корреляции:
1-й способ. Найти ошибку коэффициента корреляции (mrxy) и критерий t по формулам:
Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р > 99,9%.
2-й способ. Достоверность коэффициента корреляции оценивается по таблице «Стандартные коэффициенты корреляции» (см. приложение 1). При числе степеней свободы (n — 2)=6 — 2=4, наш расчетный коэффициент корреляции rxу = + 0,99 больше табличного (rтабл = + 0,917 при р = 99%).
Вывод. Чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная: rху = + 0,99, р > 99,9%).
на применение рангового метода
Задание: методом рангов установить направление и силу связи между стажем работы в годах и частотой травм, если получены следующие данные:
| Стаж работы в годах | Число травм на 100 работающих |
| до 1 года 1-2 3-4 5-6 7 и более | 24 16 12 12 6 |
Обоснование выбора метода: для решения задачи может быть выбран только метод ранговой корреляции, т.к. первый ряд признака «стаж работы в годах» имеет открытые варианты (стаж работы до 1 года и 7 и более лет), что не позволяет использовать для установления связи между сопоставляемыми признаками более точный метод — метод квадратов.
Решение. Последовательность расчетов изложена в тексте, результаты представлены в табл. 2.
| Стаж работы в годах | Число травм | Порядковые номера (ранги) | Разность рангов | Квадрат разности рангов | |
| X | Y | d(х-у) | d 2 | ||
| До 1 года | 24 | 1 | 5 | -4 | 16 |
| 1-2 | 16 | 2 | 4 | -2 | 4 |
| 3-4 | 12 | 3 | 2,5 | +0,5 | 0,25 |
| 5-6 | 12 | 4 | 2,5 | +1,5 | 2,25 |
| 7 и более | 6 | 5 | 1 | +4 | 16 |
| Σ d 2 = 38,5 | |||||
- Каждый из рядов парных признаков обозначить через «х» и через «у» (графы 1—2).
- Величину каждого из признаков заменить ранговым (порядковым) номером. Порядок раздачи рангов в ряду «x» следующий: минимальному значению признака (стаж до 1 года) присвоен порядковый номер «1», последующим вариантам этого же ряда признака соответственно в порядке увеличения 2-й, 3-й, 4-й и 5-й порядковые номера — ранги (см. графу 3).
Аналогичный порядок соблюдается при раздаче рангов второму признаку «у» (графа 4).
В тех случаях, когда встречаются несколько одинаковых по величине вариант (например, в задаче-эталоне это 12 и 12 травм на 100 работающих при стаже 3—4 года и 5—6 лет, порядковый номер обозначить средним числом из суммы их порядковых номеров. Эти данные о числе травм (12 травм) при ранжировании должны занимать 2 и 3 места, таким образом среднее число из них равно (2 + 3)/2 = 2,5.
Таким образом, числу травм «12» и «12» (признаку) следует раздать ранговые номера одинаковые — «2,5» (графа 4). - Определить разность рангов d = (х — у) — (графа 5)
- Разность рангов возвести в квадрат (d 2 ) и получить сумму квадратов разности рангов Σ d 2 (графа 6).
- Произвести расчет коэффициента ранговой корреляции по формуле:
где n — число сопоставляемых пар вариант в ряду «x» и в ряду «у»
Определить достоверность коэффициента ранговой корреляции.
1-й способ. Определить ошибку (mрху) коэффициента ранговой корреляции и оценить достоверность его с помощью критерия t:
Полученный критерий t = 5,75 соответствует вероятности безошибочного прогноза (р) больше 95 %:
рху = — 0,92; mрху = ± 0,16; t = 5,75; р > 95%
2-й способ. По таблице «Стандартных коэффициентов корреляции»: при числе степеней свободы (n — 2) = 5 — 2 = 3 наш расчетный коэффициент корреляции рху = — 0,92 больше табличного 0,878 и меньше 0,933, что соответствует вероятности безошибочного прогноза больше 95% и меньше 98%. Это позволяет считать полученный коэффициент ранговой корреляции достоверным.
Вывод. С вероятностью безошибочного прогноза (р) больше 95% установлено, что чем больше стаж работы, тем меньше частота травм (связь обратная, сильная, достоверная корреляционная: рху = — 0,92, p > 95%.
Стандартные коэффициенты корреляции, которые считаются достоверными (по Л.С. Каминскому)
| Число степеней свободы — 2 | Уровень вероятности р (%) | ||
| 95% | 98% | 99% | |
| 1 | 0,997 | 0,999 | 0,999 |
| 2 | 0,950 | 0,980 | 0,990 |
| 3 | 0,878 | 0,934 | 0,959 |
| 4 | 0,811 | 0,882 | 0,917 |
| 5 | 0,754 | 0,833 | 0,874 |
| 6 | 0,707 | 0,789 | 0,834 |
| 7 | 0,666 | 0,750 | 0,798 |
| 8 | 0,632 | 0,716 | 0,765 |
| 9 | 0,602 | 0,885 | 0,735 |
| 10 | 0,576 | 0,858 | 0,708 |
| 11 | 0,553 | 0,634 | 0,684 |
| 12 | 0,532 | 0,612 | 0,661 |
| 13 | 0,514 | 0,592 | 0,641 |
| 14 | 0,497 | 0,574 | 0,623 |
| 15 | 0,482 | 0,558 | 0,606 |
| 16 | 0,468 | 0,542 | 0,590 |
| 17 | 0,456 | 0,528 | 0,575 |
| 18 | 0,444 | 0,516 | 0,561 |
| 19 | 0,433 | 0,503 | 0,549 |
| 20 | 0,423 | 0,492 | 0,537 |
| 25 | 0,381 | 0,445 | 0,487 |
| 30 | 0,349 | 0,409 | 0,449 |
Применение методов статистического анализа для изучения общественного здоровья и здравоохранения. Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., «Гэотар-Медиа», 2007, учебное пособие для вузов
- Власов В.В. Эпидемиология. — М.: ГЭОТАР-МЕД, 2004. — 464 с.
- Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
- Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. — М.: Медицина, 2003. — 368 с.
- Миняев В.А., Вишняков Н.И. и др. Социальная медицина и организация здравоохранения (Руководство в 2 томах). — СПб, 1998. -528 с.
- Кучеренко В.З., Агарков Н.М. и др.Социальная гигиена и организация здравоохранения (Учебное пособие) — Москва, 2000. — 432 с.
- С. Гланц. Медико-биологическая статистика. Пер с англ. — М., Практика, 1998. — 459 с.
Источник