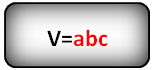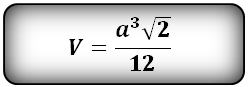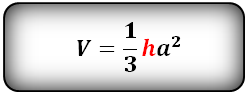Какие способы определения объема вы знаете

ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1

Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1 . Определите цену деления мензурки.
2 . Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3 . Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201 ), и снова измерьте объём жидкости.
4 . Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5 . Результаты измерений запишите в таблицу 9 .
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202 ). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.

Таблица 9 .

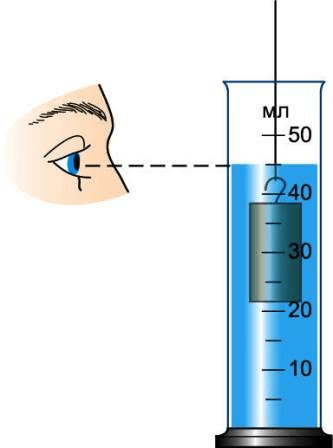
рис. 201

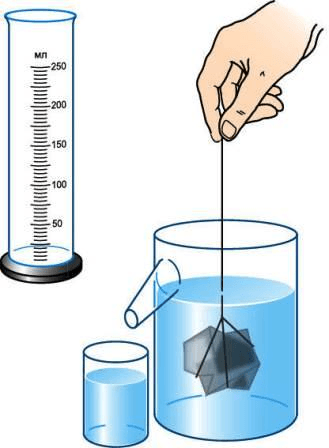
рис. 202

Решение

Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэто­му для измерения объема воспользуемся мензуркой. Тело, полностью погружён­ное в жидкость, вытесняет объём жидкости, кото­рый равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следую­щим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
$V = V_ <2>— V_<1>$ , где $V_<2>$ − объём воды и тела, $V_<1>$ − начальный объём воды в мензурке.

1. Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
   Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
   На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
   Таким образом, цена каждого деления будет равна
   $\frac<30 - 20><2>= \frac<10><2>$ = 5 мл.
2. В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70 $см^<3>$ .
3. Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
   Вычисления.
   $V_ <бр>= 95 — 70 = 25 см^<3>$
   $V_ <ц>= 85 — 65 = 20 см^<3>$
   $V_ <ш>= 75 — 60 = 15 см^<3>$
4. Результаты измерений запишем в таблицу 9 .

№ опыта	Название тела	Начальный объём воды в мензурке $V_<1>, см^<3>$	Объём воды и тела $V_<2>, см^<3>$	Объём тела V, $см^<3>$ $V = V_<2>-V <1>$
1	Брусок	70	95	25
2	Цилиндр	65	85	20
3	Шарик	60	75	15

Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.

Источник

Объемы геометрических тел

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

• V сохраняется при движениях.
• V удовлетворяет принципу Кавальери.
• Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
• Объем прямоугольного параллелепипеда V = abc.

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

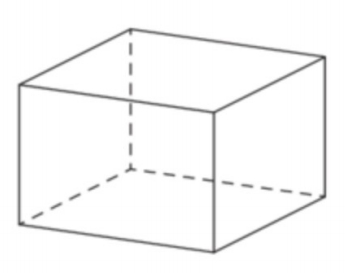
Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

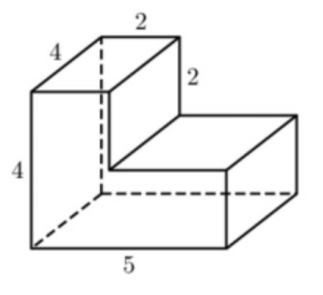
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

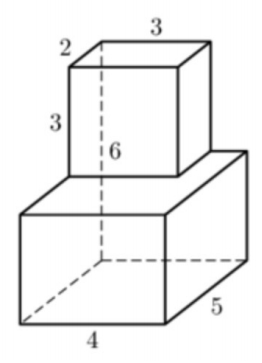
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Разберем, как можно вычислять объемы изучаемых в школе фигур.

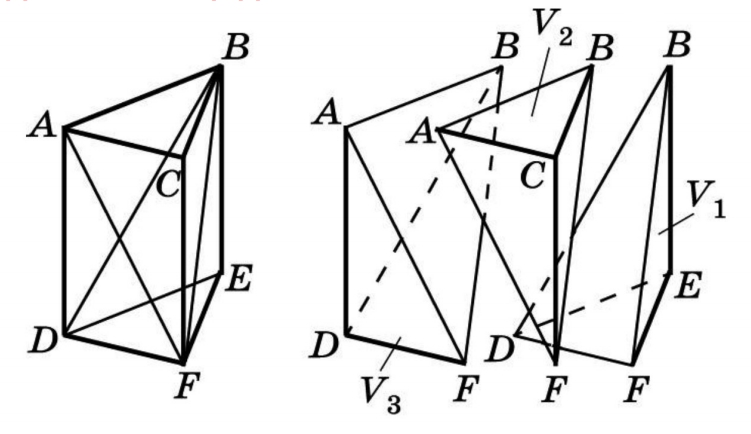
Объем призмы

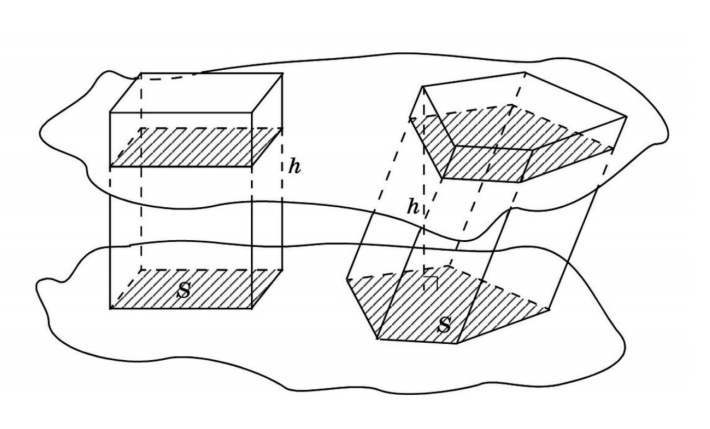
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф₂) поместим прямоугольный параллелепипед (Ф₁), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

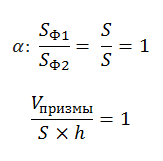
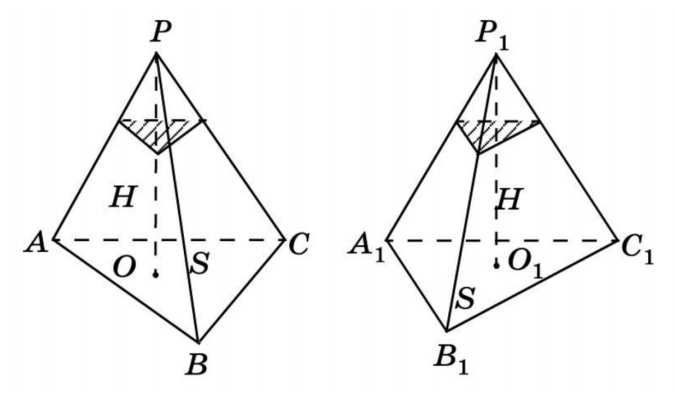
Объем пирамиды

Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

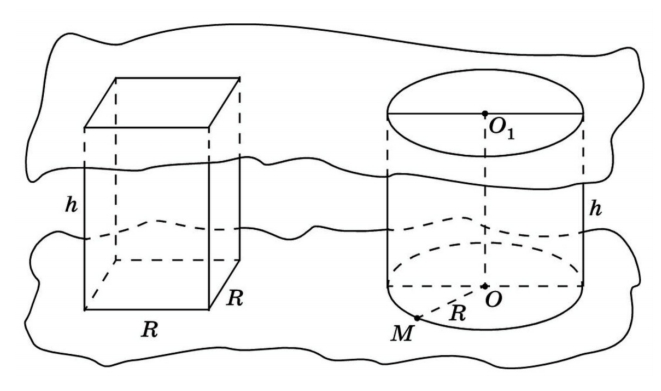
Объем цилиндра

Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

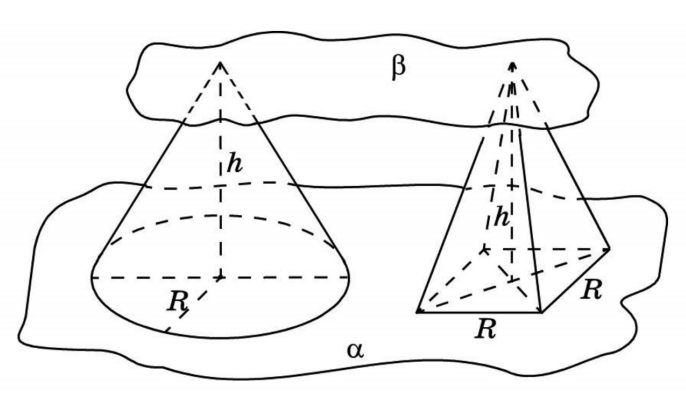
Объем конуса

Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте «Математические этюды» , где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.

Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR 2 . Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x 2 . Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R 2 — x 2 ).

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

Источник

Все формулы объемов геометрических тел

1. Расчет объема куба

a — сторона куба

Формула объема куба, (V):

2. Найти по формуле, объем прямоугольного параллелепипеда

a , b , c — стороны параллелепипеда

Еще иногда сторону параллелепипеда, называют ребром.

Формула объема параллелепипеда, (V):

3. Формула для вычисления объема шара, сферы

R — радиус шара

По формуле, если дан радиус, можно найти объема шара, (V):

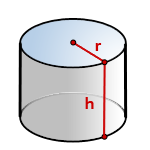
4. Как вычислить объем цилиндра ?

h — высота цилиндра

r — радиус основания

По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V):

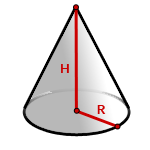
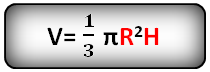
5. Как найти объем конуса ?

R — радиус основания

H — высота конуса

Формула объема конуса, если известны радиус и высота (V):

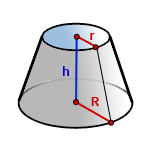
7. Формула объема усеченного конуса

r — радиус верхнего основания

R — радиус нижнего основания

h — высота конуса

Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

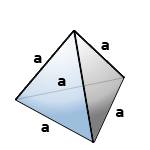
8. Объем правильного тетраэдра

Правильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.

а — ребро тетраэдра

Формула, для расчета объема правильного тетраэдра (V):

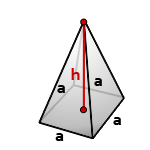
9. Объем правильной четырехугольной пирамиды

Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

a — сторона основания

h — высота пирамиды

Формула для вычисления объема правильной четырехугольной пирамиды, (V):

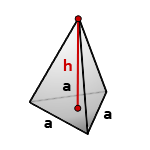
10. Объем правильной треугольной пирамиды

Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

a — сторона основания

h — высота пирамиды

Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V):

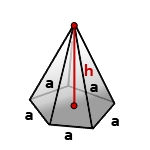
11. Найти объем правильной пирамиды

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

h — высота пирамиды

a — сторона основания пирамиды

n — количество сторон многоугольника в основании

Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):

Источник