- Способы образования неизменяемых систем
- 3. Способы образования неизменяемых систем
- 4. Понятие о мгновенно изменяемых системах
- Способы образования геометрически неизменяемой системы
- Способы образования неизменяемых систем
- 3. Способы образования неизменяемых систем
- 4. Понятие о мгновенно изменяемых системах
Способы образования неизменяемых систем
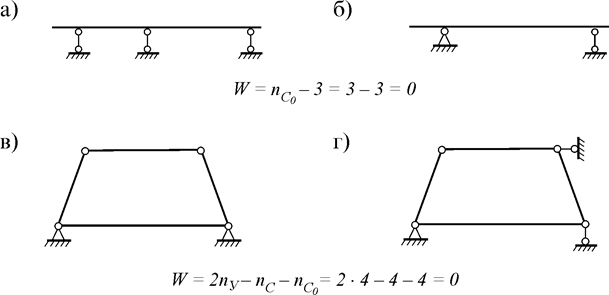
Выполнение условий, рассмотренных выше необходимо, но не достаточно. Например, число степеней свободы систем (рис. 2.7 а, в) одинаково: W=0, поэтому необходимое условие их геометрической неизменяемости выполняется. Но, тем не менее, они оба геометрически изменяемы. Причиной их изменяемости является неправильная установка связей. Для того чтобы они стали неизменяемыми, одну связь в этих системах нужно переставить (рис. 2.7 б, г).
Из этих примеров следует, что для полной уверенности в неизменяемости системы нужна дополнительная проверка системы – проверка геометрической структуры. Ее суть заключается в проверке способов объединения элементов между собой и с землей. Для такой проверки необходимо:
– выделить в системе неизменяемые фигуры – диски;
– последовательно объединять эти диски между собой, используя способы образования неизменяемых систем.
Рассмотрим простейшие способы образования геометрически неизменяемых систем:
1. Новый узел к диску должен добавляться способом диады – двумя непараллельными стержнями (рис. 2.8 а).
2. Два диска должны объединяться:
– способом триады – тремя не параллельными и не пересекающимися в одной точке связями (рис. 2.8 в);
– одним шарниром и одной связью (рис. 2.8 б). Этот способ вытекает из способа триады;
3. Три диска должны объединяться тремя шарнирами, не лежащими на одной прямой (рис. 2.8 г). Шарниры могут быть условными (рис. 2.8 д).

Источник
3. Способы образования неизменяемых систем
Выполнение условий, рассмотренных выше необходимо, но не достаточно. Например, число степеней свободы систем (рис. 2.7 а, в) одинаково: W=0, поэтому необходимое условие их геометрической неизменяемости выполняется. Но, тем не менее, они оба геометрически изменяемы. Причиной их изменяемости является неправильная установка связей. Для того чтобы они стали неизменяемыми, одну связь в этих системах нужно переставить (рис. 2.7 б, г).
Из этих примеров следует, что для полной уверенности в неизменяемости системы нужна дополнительная проверка системы – проверка геометрической структуры. Ее суть заключается в проверке способов объединения элементов между собой и с землей. Для такой проверки необходимо:
– выделить в системе неизменяемые фигуры – диски;
– последовательно объединять эти диски между собой, используя способы образования неизменяемых систем.
Рассмотрим простейшие способы образования геометрически неизменяемых систем:
1. Новый узел к диску должен добавляться способом диады – двумя непараллельными стержнями (рис. 2.8 а).
2. Два диска должны объединяться:
– способом триады – тремя не параллельными и не пересекающимися в одной точке связями (рис. 2.8 в);
– одним шарниром и одной связью (рис. 2.8 б). Этот способ вытекает из способа триады;
3. Три диска должны объединяться тремя шарнирами, не лежащими на одной прямой (рис. 2.8 г). Шарниры могут быть условными (рис. 2.8 д).
4. Понятие о мгновенно изменяемых системах
Расчетная схема любого инженерного сооружения не должна быть изменяемой или мгновенно изменяемой. Если изменяемость системы обычно возникает из-за недостатка связей, то мгновенная изменяемость возникает при их неправильной установке (рис. 2.9 а, г, д, е).
Обнаружить мгновенную изменяемость очень важно уже на этапе кинематического анализа, так как позволяет вносить коррективы в расчетную схему сооружения.
В качестве примера рассмотрим балку (рис. 2.9 а) и выясним, почему же она является мгновенно изменяемой.
1. При действии на эту балку сосредоточенной силы P ее положение изменится (рис. 2.9 б). Запишем условие равновесия системы сходящихся сил в точке 
N = 
Если в этой формуле =0, т.е. когда стержни AB и BC лежат на одной прямой, то N=. Таким образом, мгновенная изменяемость опасна тем, что усилия в элементах системы могут быть очень большими.
2. Если в последней формуле примем P=0, внутреннее усилие становится неопределенным: N=0/0.
Этот результат лежит в основе метода нулевой нагрузки. Суть этого метода заключается в следующем:
– удалить все силы, действующие на систему;
– вычислить внутренние усилия. Если они все (включая и опорные реакции) будут равны нулю, то система неизменяема. Если же хотя бы одно усилие будет неопределенным (типа 0/0), то данная система является мгновенно изменяемой.
Общие выводы. Расчетная схема сооружения должна быть геометрически неизменяемой. С целью проверки геометрической неизменяемости проводится кинематический анализ, состоящий из двух этапов:
1) количественный анализ – проводится по основной формуле кинематического анализа; должно выполняться условие W 0;
2) качественный анализ – проводится с использованием способов образования геометрически неизменяемых систем.
Источник
Способы образования геометрически неизменяемой системы
Кинематический анализ расчетных схем сооружений
Различают три типа расчетных схем:
1) геометрически неизменяемые системы – это системы, в которых перемещения возможны только при деформации стержней.,
2) геометрически изменяемые системы – это системы, в которых перемещения возможны без деформации стержней (механизмы).
3) мгновенно изменяемые системы – системы допускающие бесконечно малые перемещения стержней, при которых возникают большие внутренние усилия.
Мгновенно изменяемые и геометрически изменяемые системы в сооружениях не применяются.
Изменяемость системы характеризуется числом степеней свободы, которое равно числу независимых геометрических параметров, полностью определяющих положение всех элементов этой системы.
Кинематический анализ позволяет установить, является ли заданная система геометрически изменяемой или геометрически неизменяемой и состоит из двух этапов: определения числа степеней свободы сооружения и анализа геометрической структуры.
1 этап. – Определение числа степеней свободы стержневой системы по формуле Чебышева:
где W – число степеней свободы системы, D – количество дисков, Ш – число простых одиночных шарниров, С0 – количество опорных стержней.
Диск — геометрически неизменяемая часть сооружения, состоящая из одного или нескольких жестко связанных элементов, не изменяющая на плоскости своей формы и размеров. Диск на плоскости имеет три степени свободы
Простой шарнир соединяет два стержня с помощью шарнира и отнимает у системы две степени свободы.
Кратный шарнир соединяет s стержней и эквивалентен (s – 1) простому шарниру.
Кинематическая связь (стержень, опорная связь) уничтожает одну степень свободы.
В зависимости от значения W возможны три случая:
1. W>0 — система подвижная, т.е. геометрически изменяемая;
2. W=0 — система геометрически неизменяема и статически определима;
Источник
Способы образования неизменяемых систем
Выполнение условий, рассмотренных выше необходимо, но не достаточно. Например, число степеней свободы систем (рис. 2.7 а, в) одинаково: W=0, поэтому необходимое условие их геометрической неизменяемости выполняется. Но, тем не менее, они оба геометрически изменяемы. Причиной их изменяемости является неправильная установка связей. Для того чтобы они стали неизменяемыми, одну связь в этих системах нужно переставить (рис. 2.7 б, г).
Из этих примеров следует, что для полной уверенности в неизменяемости системы нужна дополнительная проверка системы – проверка геометрической структуры. Ее суть заключается в проверке способов объединения элементов между собой и с землей. Для такой проверки необходимо:
– выделить в системе неизменяемые фигуры – диски;
– последовательно объединять эти диски между собой, используя способы образования неизменяемых систем.
Рассмотрим простейшие способы образования геометрически неизменяемых систем:
1. Новый узел к диску должен добавляться способом диады – двумя непараллельными стержнями (рис. 2.8 а).
2. Два диска должны объединяться:
– способом триады – тремя не параллельными и не пересекающимися в одной точке связями (рис. 2.8 в);
– одним шарниром и одной связью (рис. 2.8 б). Этот способ вытекает из способа триады;
3. Три диска должны объединяться тремя шарнирами, не лежащими на одной прямой (рис. 2.8 г). Шарниры могут быть условными (рис. 2.8 д).
Источник
3. Способы образования неизменяемых систем
Выполнение условий, рассмотренных выше необходимо, но не достаточно. Например, число степеней свободы систем (рис. 2.7 а, в) одинаково: W=0, поэтому необходимое условие их геометрической неизменяемости выполняется. Но, тем не менее, они оба геометрически изменяемы. Причиной их изменяемости является неправильная установка связей. Для того чтобы они стали неизменяемыми, одну связь в этих системах нужно переставить (рис. 2.7 б, г).
Из этих примеров следует, что для полной уверенности в неизменяемости системы нужна дополнительная проверка системы – проверка геометрической структуры. Ее суть заключается в проверке способов объединения элементов между собой и с землей. Для такой проверки необходимо:
– выделить в системе неизменяемые фигуры – диски;
– последовательно объединять эти диски между собой, используя способы образования неизменяемых систем.
Рассмотрим простейшие способы образования геометрически неизменяемых систем:
1. Новый узел к диску должен добавляться способом диады – двумя непараллельными стержнями (рис. 2.8 а).
2. Два диска должны объединяться:
– способом триады – тремя не параллельными и не пересекающимися в одной точке связями (рис. 2.8 в);
– одним шарниром и одной связью (рис. 2.8 б). Этот способ вытекает из способа триады;
3. Три диска должны объединяться тремя шарнирами, не лежащими на одной прямой (рис. 2.8 г). Шарниры могут быть условными (рис. 2.8 д).
4. Понятие о мгновенно изменяемых системах
Расчетная схема любого инженерного сооружения не должна быть изменяемой или мгновенно изменяемой. Если изменяемость системы обычно возникает из-за недостатка связей, то мгновенная изменяемость возникает при их неправильной установке (рис. 2.9 а, г, д, е).
Обнаружить мгновенную изменяемость очень важно уже на этапе кинематического анализа, так как позволяет вносить коррективы в расчетную схему сооружения.
В качестве примера рассмотрим балку (рис. 2.9 а) и выясним, почему же она является мгновенно изменяемой.
1. При действии на эту балку сосредоточенной силы P ее положение изменится (рис. 2.9 б). Запишем условие равновесия системы сходящихся сил в точке 
N = 
Если в этой формуле =0, т.е. когда стержни AB и BC лежат на одной прямой, то N=. Таким образом, мгновенная изменяемость опасна тем, что усилия в элементах системы могут быть очень большими.
2. Если в последней формуле примем P=0, внутреннее усилие становится неопределенным: N=0/0.
Этот результат лежит в основе метода нулевой нагрузки. Суть этого метода заключается в следующем:
– удалить все силы, действующие на систему;
– вычислить внутренние усилия. Если они все (включая и опорные реакции) будут равны нулю, то система неизменяема. Если же хотя бы одно усилие будет неопределенным (типа 0/0), то данная система является мгновенно изменяемой.
Общие выводы. Расчетная схема сооружения должна быть геометрически неизменяемой. С целью проверки геометрической неизменяемости проводится кинематический анализ, состоящий из двух этапов:
1) количественный анализ – проводится по основной формуле кинематического анализа; должно выполняться условие W 0;
2) качественный анализ – проводится с использованием способов образования геометрически неизменяемых систем.
Источник